
Question Number 216670 by ahmed2025 last updated on 15/Feb/25
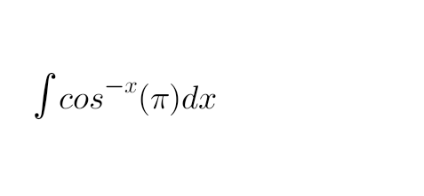
Answered by shunmisaki007 last updated on 15/Feb/25
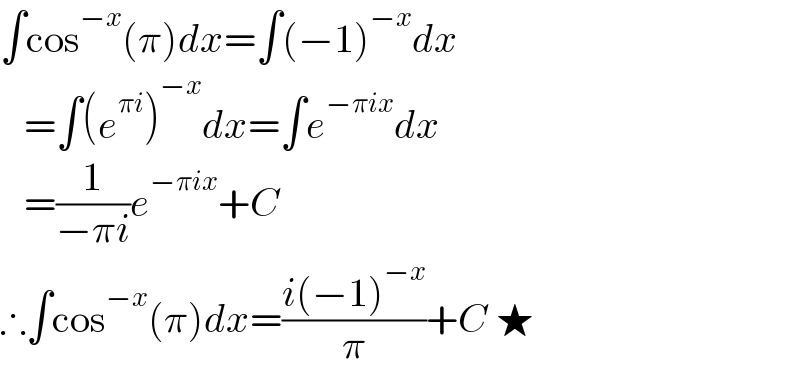
$$\int\mathrm{cos}^{−{x}} \left(\pi\right){dx}=\int\left(−\mathrm{1}\right)^{−{x}} {dx} \\ $$$$\:\:\:=\int\left({e}^{\pi{i}} \right)^{−{x}} {dx}=\int{e}^{−\pi{ix}} {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{−\pi{i}}{e}^{−\pi{ix}} +{C} \\ $$$$\therefore\int\mathrm{cos}^{−{x}} \left(\pi\right){dx}=\frac{{i}\left(−\mathrm{1}\right)^{−{x}} }{\pi}+{C}\:\bigstar \\ $$
Answered by MrGaster last updated on 15/Feb/25
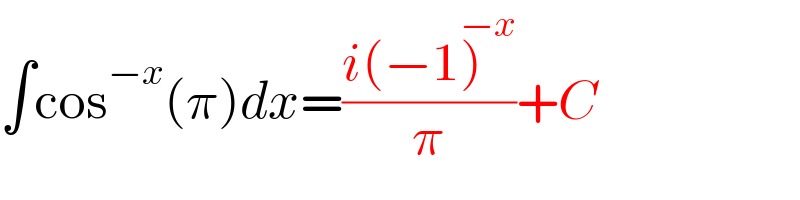
$$\int\mathrm{cos}^{−{x}} \left(\pi\right){dx}=\frac{{i}\left(−\mathrm{1}\overset{−{x}} {\right)}}{\pi}+{C} \\ $$
Answered by Ghisom last updated on 16/Feb/25
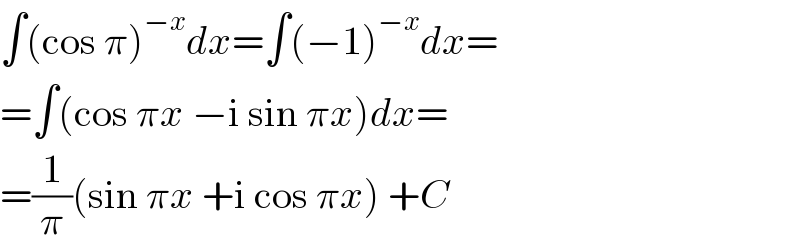
$$\int\left(\mathrm{cos}\:\pi\right)^{−{x}} {dx}=\int\left(−\mathrm{1}\right)^{−{x}} {dx}= \\ $$$$=\int\left(\mathrm{cos}\:\pi{x}\:−\mathrm{i}\:\mathrm{sin}\:\pi{x}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\pi}\left(\mathrm{sin}\:\pi{x}\:+\mathrm{i}\:\mathrm{cos}\:\pi{x}\right)\:+{C} \\ $$
