
Question Number 216665 by Tawa11 last updated on 14/Feb/25
Commented by Tawa11 last updated on 14/Feb/25

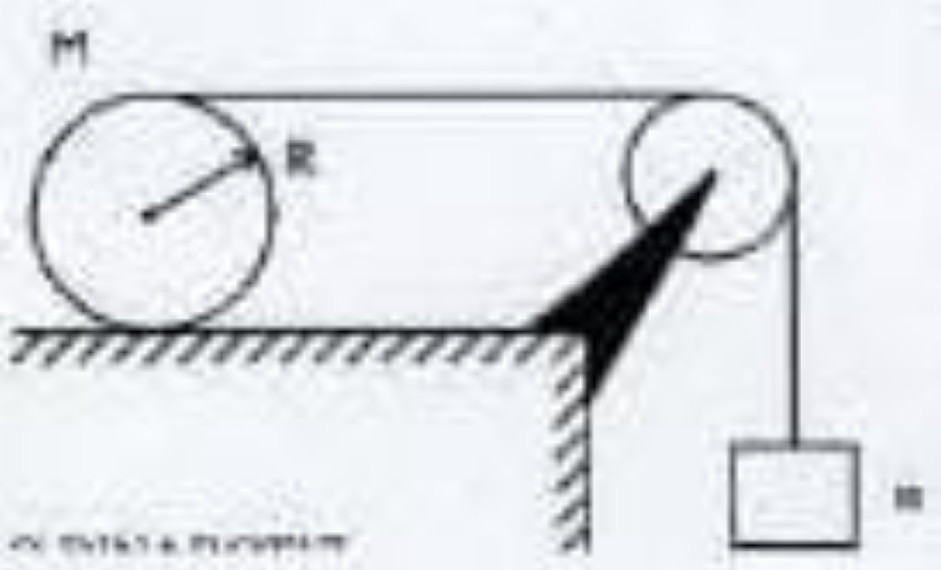
In the figure, a cylinder of mass M, radius R and moment of inertia I = (MR²)/2 is placed on a horizontal table. The rope wound around the cylinder passes over an ideal massless pulley and is then tied to a block of mass, m = 2M. At the instant shown, the block is falling and the cylinder rolls without slipping, unwinding the rope. Find: a) the acceleration of the block, b) the acceleration of the center of mass of the spool
Answered by mr W last updated on 17/Feb/25
Commented by mr W last updated on 16/Feb/25
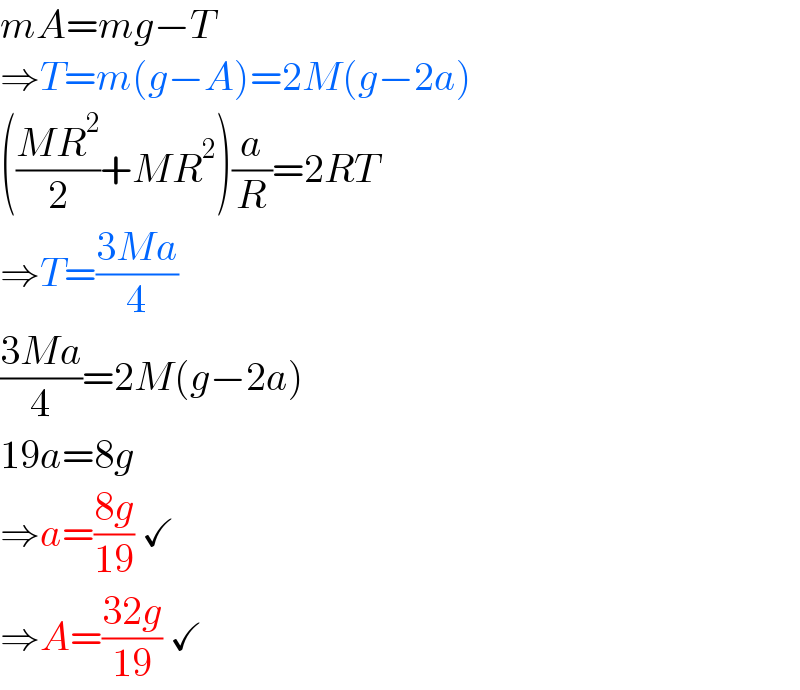
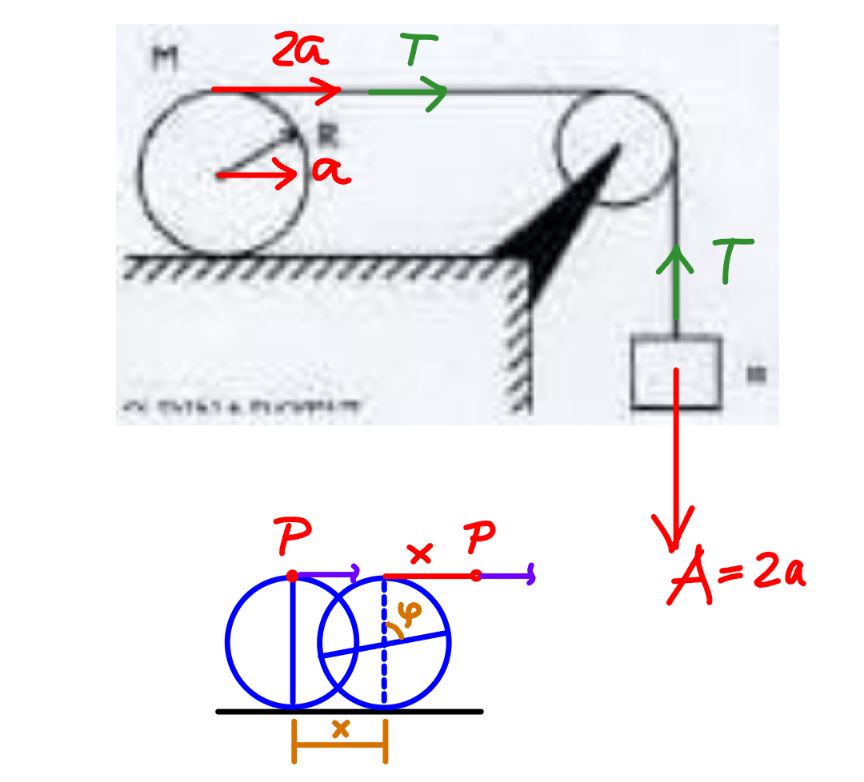
$${mA}={mg}−{T} \\ $$$$\Rightarrow{T}={m}\left({g}−{A}\right)=\mathrm{2}{M}\left({g}−\mathrm{2}{a}\right) \\ $$$$\left(\frac{{MR}^{\mathrm{2}} }{\mathrm{2}}+{MR}^{\mathrm{2}} \right)\frac{{a}}{{R}}=\mathrm{2}{RT} \\ $$$$\Rightarrow{T}=\frac{\mathrm{3}{Ma}}{\mathrm{4}} \\ $$$$\frac{\mathrm{3}{Ma}}{\mathrm{4}}=\mathrm{2}{M}\left({g}−\mathrm{2}{a}\right) \\ $$$$\mathrm{19}{a}=\mathrm{8}{g} \\ $$$$\Rightarrow{a}=\frac{\mathrm{8}{g}}{\mathrm{19}}\:\checkmark \\ $$$$\Rightarrow{A}=\frac{\mathrm{32}{g}}{\mathrm{19}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 15/Feb/25

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 15/Feb/25

$${answer}\:{correct}? \\ $$
Commented by Tawa11 last updated on 16/Feb/25
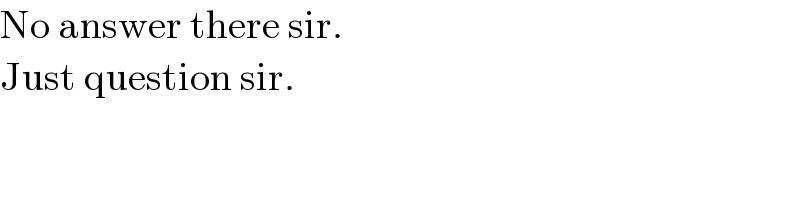
$$\mathrm{No}\:\mathrm{answer}\:\mathrm{there}\:\mathrm{sir}. \\ $$$$\mathrm{Just}\:\mathrm{question}\:\mathrm{sir}. \\ $$
