
Question Number 216655 by abdelsalam last updated on 14/Feb/25
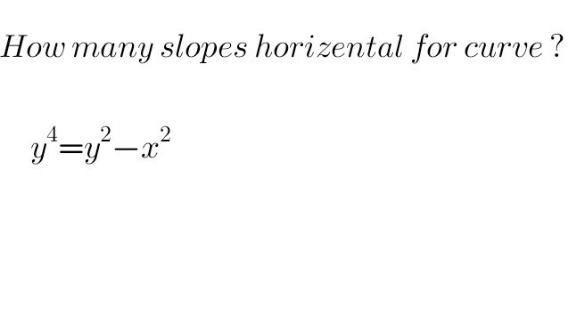
Answered by issac last updated on 14/Feb/25
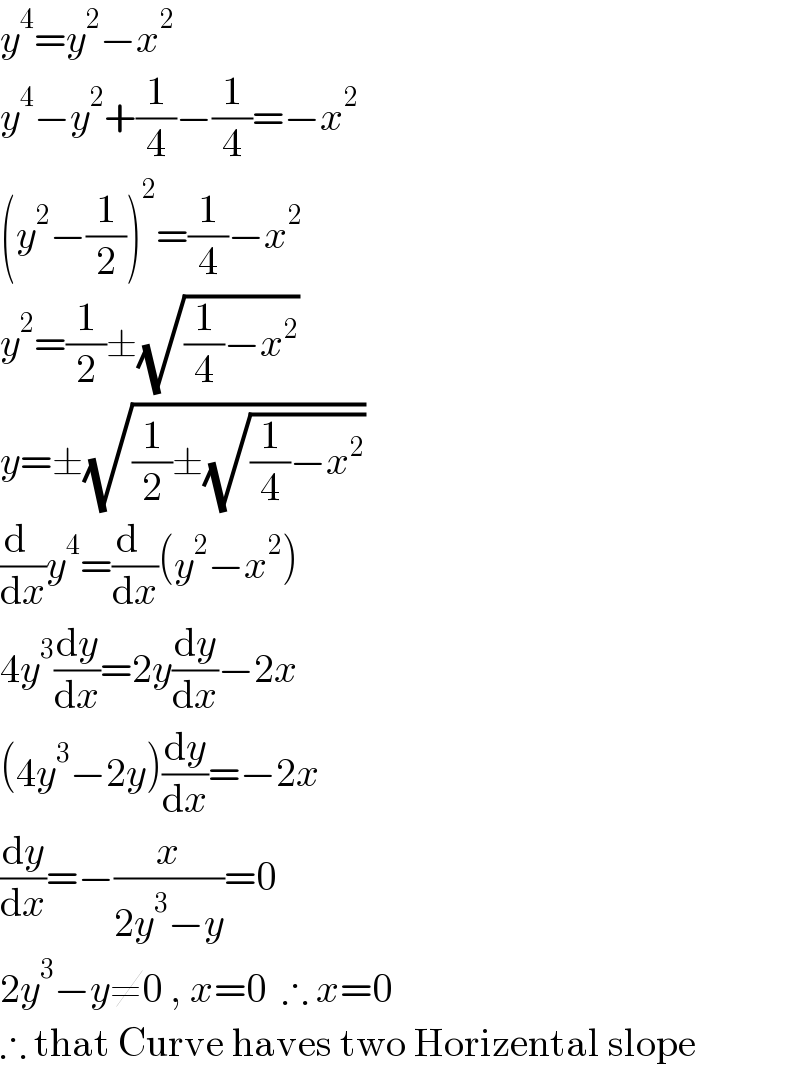
$${y}^{\mathrm{4}} ={y}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$${y}^{\mathrm{4}} −{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}=−{x}^{\mathrm{2}} \\ $$$$\left({y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}−{x}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−{x}^{\mathrm{2}} } \\ $$$${y}=\pm\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{d}\:\:}{\mathrm{d}{x}}{y}^{\mathrm{4}} =\frac{\mathrm{d}\:\:}{\mathrm{d}{x}}\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{y}^{\mathrm{3}} \frac{\mathrm{d}{y}}{\mathrm{d}{x}}=\mathrm{2}{y}\frac{\mathrm{d}{y}}{\mathrm{d}{x}}−\mathrm{2}{x} \\ $$$$\left(\mathrm{4}{y}^{\mathrm{3}} −\mathrm{2}{y}\right)\frac{\mathrm{d}{y}}{\mathrm{d}{x}}=−\mathrm{2}{x} \\ $$$$\frac{\mathrm{d}{y}}{\mathrm{d}{x}}=−\frac{{x}}{\mathrm{2}{y}^{\mathrm{3}} −{y}}=\mathrm{0} \\ $$$$\mathrm{2}{y}^{\mathrm{3}} −{y}\neq\mathrm{0}\:,\:{x}=\mathrm{0}\:\:\therefore\:{x}=\mathrm{0}\: \\ $$$$\therefore\:\mathrm{that}\:\mathrm{Curve}\:\mathrm{haves}\:\mathrm{two}\:\mathrm{Horizental}\:\mathrm{slope} \\ $$
