Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 216621 by Tawa11 last updated on 12/Feb/25

Answered by A5T last updated on 12/Feb/25

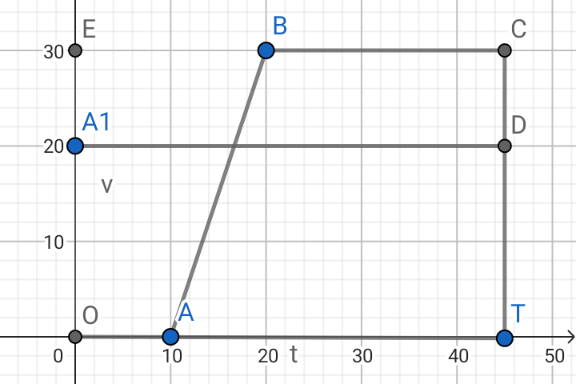
Commented by A5T last updated on 12/Feb/25

[OA_1 DT]=[ABCT] when both cars meet at time t ⇒20t=((30(t−20+t−10))/2)⇒4t=3(2t−30) ⇒t=45s⇒ s=20×45=900m ⇒Sports car overtakes first car 45s and 900m after car overtakes stationary sports car.

$$\left[\mathrm{OA}_{\mathrm{1}} \mathrm{DT}\right]=\left[\mathrm{ABCT}\right]\:\mathrm{when}\:\mathrm{both}\:\mathrm{cars}\:\mathrm{meet}\:\mathrm{at}\:\mathrm{time}\:\mathrm{t} \\ $$$$\Rightarrow\mathrm{20t}=\frac{\mathrm{30}\left(\mathrm{t}−\mathrm{20}+\mathrm{t}−\mathrm{10}\right)}{\mathrm{2}}\Rightarrow\mathrm{4t}=\mathrm{3}\left(\mathrm{2t}−\mathrm{30}\right) \\ $$$$\Rightarrow\mathrm{t}=\mathrm{45s}\Rightarrow\:\mathrm{s}=\mathrm{20}×\mathrm{45}=\mathrm{900m} \\ $$$$\Rightarrow\mathrm{Sports}\:\mathrm{car}\:\mathrm{overtakes}\:\mathrm{first}\:\mathrm{car}\:\mathrm{45s}\:\mathrm{and}\:\mathrm{900m}\: \\ $$$$\mathrm{after}\:\mathrm{car}\:\mathrm{overtakes}\:\mathrm{stationary}\:\mathrm{sports}\:\mathrm{car}. \\ $$

Commented by Tawa11 last updated on 12/Feb/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by mr W last updated on 12/Feb/25

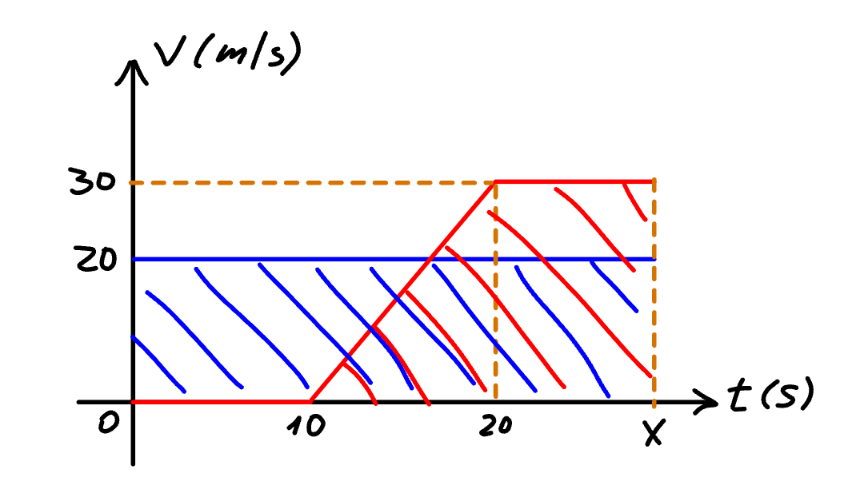
Commented by mr W last updated on 12/Feb/25

distance is the area under the corresponding v−t curve. d=20x=((30×10)/2)+30(x−20) ⇒x=45 s ⇒d=20×45=900 m

$${distance}\:{is}\:{the}\:{area}\:{under}\:{the} \\ $$$${corresponding}\:{v}−{t}\:{curve}. \\ $$$${d}=\mathrm{20}{x}=\frac{\mathrm{30}×\mathrm{10}}{\mathrm{2}}+\mathrm{30}\left({x}−\mathrm{20}\right) \\ $$$$\Rightarrow{x}=\mathrm{45}\:{s} \\ $$$$\Rightarrow{d}=\mathrm{20}×\mathrm{45}=\mathrm{900}\:{m} \\ $$

Commented by Tawa11 last updated on 12/Feb/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 14/Feb/25

Sirs, can this be solved without graph?

$$\mathrm{Sirs},\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{without}\:\mathrm{graph}? \\ $$

Commented by mr W last updated on 15/Feb/25

the solution above is without graph! or you don′t understand it without the graph?

$${the}\:{solution}\:{above}\:{is}\:{without} \\ $$$${graph}!\:{or}\:{you}\:{don}'{t}\:{understand}\:{it} \\ $$$${without}\:{the}\:{graph}? \\ $$

Commented by Tawa11 last updated on 15/Feb/25

I mean, can we solve analytically without solving from graph? Can we solve the distance and time without drawing graph (v−t graph)?

$$\mathrm{I}\:\mathrm{mean},\:\mathrm{can}\:\mathrm{we}\:\mathrm{solve}\:\mathrm{analytically} \\ $$$$\mathrm{without}\:\mathrm{solving}\:\mathrm{from}\:\mathrm{graph}? \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{and}\:\mathrm{time} \\ $$$$\mathrm{without}\:\mathrm{drawing}\:\mathrm{graph}\:\left(\mathrm{v}−\mathrm{t}\:\mathrm{graph}\right)? \\ $$

Commented by mr W last updated on 15/Feb/25

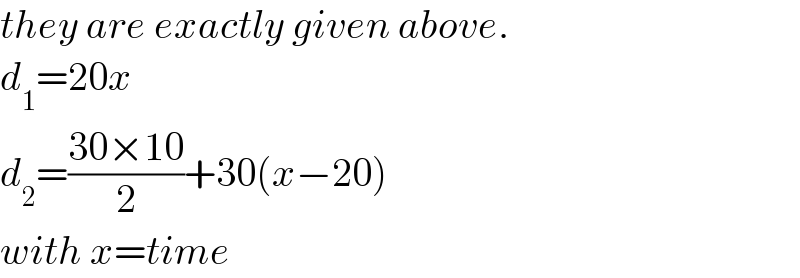
they are exactly given above. d_1 =20x d_2 =((30×10)/2)+30(x−20) with x=time

$${they}\:{are}\:{exactly}\:{given}\:{above}. \\ $$$${d}_{\mathrm{1}} =\mathrm{20}{x} \\ $$$${d}_{\mathrm{2}} =\frac{\mathrm{30}×\mathrm{10}}{\mathrm{2}}+\mathrm{30}\left({x}−\mathrm{20}\right) \\ $$$${with}\:{x}={time} \\ $$

Commented by Tawa11 last updated on 15/Feb/25

Ohh, I grab sir. Thanks sir.

$$\mathrm{Ohh},\:\mathrm{I}\:\mathrm{grab}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com