
Question Number 216593 by Tawa11 last updated on 11/Feb/25
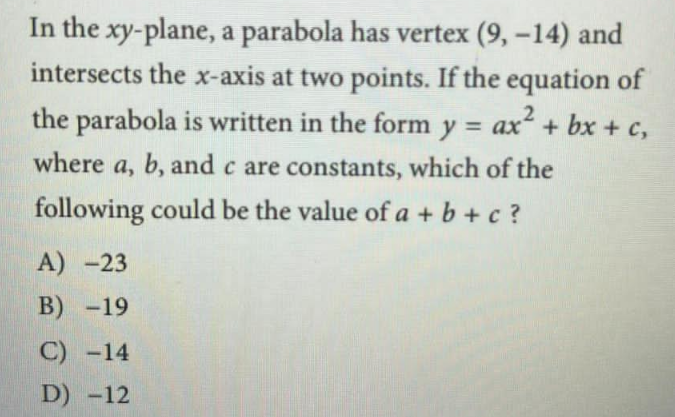
Answered by A5T last updated on 11/Feb/25
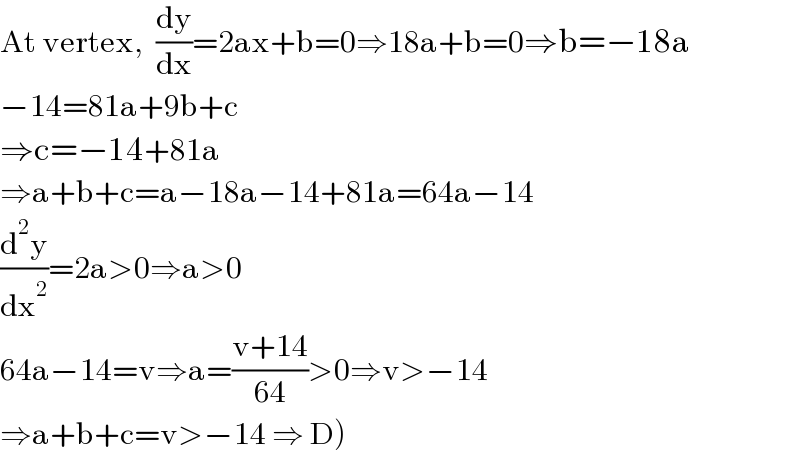
$$\mathrm{At}\:\mathrm{vertex},\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{2ax}+\mathrm{b}=\mathrm{0}\Rightarrow\mathrm{18a}+\mathrm{b}=\mathrm{0}\Rightarrow\mathrm{b}=−\mathrm{18a} \\ $$$$−\mathrm{14}=\mathrm{81a}+\mathrm{9b}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{c}=−\mathrm{14}+\mathrm{81a} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{a}−\mathrm{18a}−\mathrm{14}+\mathrm{81a}=\mathrm{64a}−\mathrm{14} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=\mathrm{2a}>\mathrm{0}\Rightarrow\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{64a}−\mathrm{14}=\mathrm{v}\Rightarrow\mathrm{a}=\frac{\mathrm{v}+\mathrm{14}}{\mathrm{64}}>\mathrm{0}\Rightarrow\mathrm{v}>−\mathrm{14} \\ $$$$\left.\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{v}>−\mathrm{14}\:\Rightarrow\:\mathrm{D}\right) \\ $$
Commented by Tawa11 last updated on 12/Feb/25

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by mr W last updated on 12/Feb/25
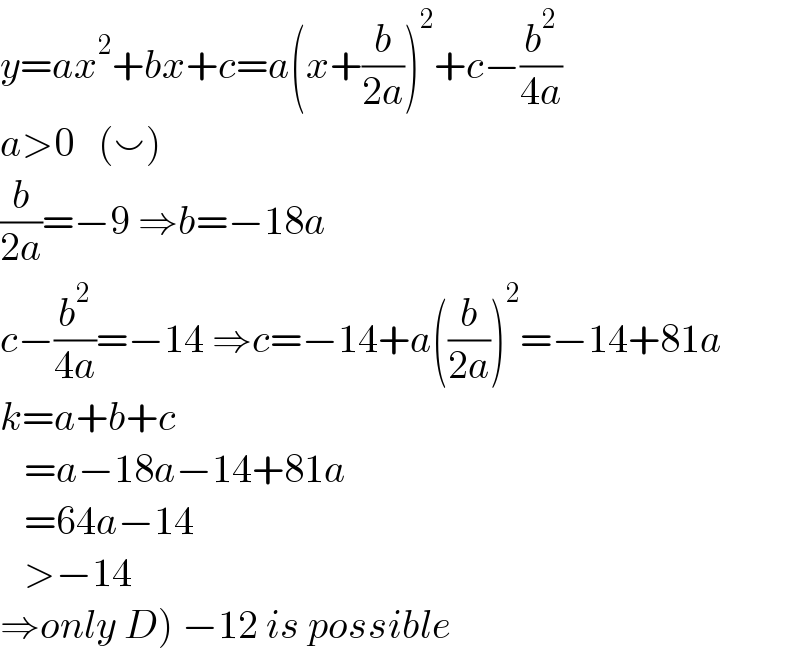
$${y}={ax}^{\mathrm{2}} +{bx}+{c}={a}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +{c}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$${a}>\mathrm{0}\:\:\:\left(\smallsmile\right) \\ $$$$\frac{{b}}{\mathrm{2}{a}}=−\mathrm{9}\:\Rightarrow{b}=−\mathrm{18}{a} \\ $$$${c}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}}=−\mathrm{14}\:\Rightarrow{c}=−\mathrm{14}+{a}\left(\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} =−\mathrm{14}+\mathrm{81}{a} \\ $$$${k}={a}+{b}+{c} \\ $$$$\:\:\:={a}−\mathrm{18}{a}−\mathrm{14}+\mathrm{81}{a} \\ $$$$\:\:\:=\mathrm{64}{a}−\mathrm{14} \\ $$$$\:\:\:>−\mathrm{14} \\ $$$$\left.\Rightarrow{only}\:{D}\right)\:−\mathrm{12}\:{is}\:{possible} \\ $$
Commented by Tawa11 last updated on 12/Feb/25

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
