Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 216525 by Mingma last updated on 10/Feb/25

Answered by Rasheed.Sindhi last updated on 10/Feb/25

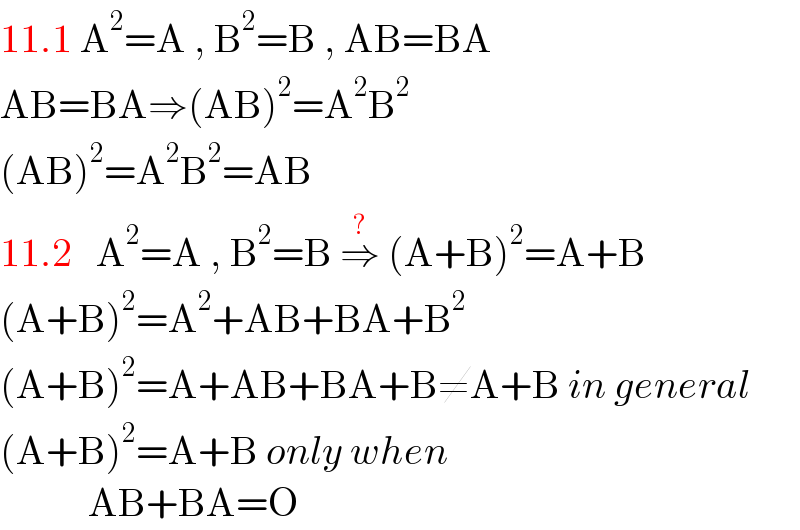
11.1 A^2 =A , B^2 =B , AB=BA AB=BA⇒(AB)^2 =A^2 B^2 (AB)^2 =A^2 B^2 =AB 11.2 A^2 =A , B^2 =B ⇒^(?) (A+B)^2 =A+B (A+B)^2 =A^2 +AB+BA+B^2 (A+B)^2 =A+AB+BA+B≠A+B in general (A+B)^2 =A+B only when AB+BA=O

$$\mathrm{11}.\mathrm{1}\:\mathrm{A}^{\mathrm{2}} =\mathrm{A}\:,\:\mathrm{B}^{\mathrm{2}} =\mathrm{B}\:,\:\mathrm{AB}=\mathrm{BA} \\ $$$$\mathrm{AB}=\mathrm{BA}\Rightarrow\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{A}^{\mathrm{2}} \mathrm{B}^{\mathrm{2}} \\ $$$$\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{A}^{\mathrm{2}} \mathrm{B}^{\mathrm{2}} =\mathrm{AB} \\ $$$$\mathrm{11}.\mathrm{2}\:\:\:\mathrm{A}^{\mathrm{2}} =\mathrm{A}\:,\:\mathrm{B}^{\mathrm{2}} =\mathrm{B}\:\overset{?} {\Rightarrow}\:\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}+\mathrm{B} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}^{\mathrm{2}} +\mathrm{AB}+\mathrm{BA}+\mathrm{B}^{\mathrm{2}} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}+\mathrm{AB}+\mathrm{BA}+\mathrm{B}\neq\mathrm{A}+\mathrm{B}\:{in}\:{general} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}+\mathrm{B}\:{only}\:{when} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{AB}+\mathrm{BA}=\mathrm{O} \\ $$

Commented by Mingma last updated on 10/Feb/25

Perfect sir! thank you!

Answered by Wuji last updated on 10/Feb/25

A^2 =A−−1 B^2 =B−−−2 AB=BA−−−3 for (AB)^2 =AB (AB)^2 =AB•AB=A(BA)B from (3) (AB)^2 =A(AB)B=A^2 B^2 (AB)^2 =AB {from(1) and (2)} check if (A+B)^2 =(A+B) (A+B)^2 =A^2 +AB+BA+B^2 =B+AB+BA+B (A+B)^2 =A+AB+BA+B=A+B+2AB (A+B)^2 =A+B+2AB ∴ A+B≠idempotent since AB=BA=0

$$\mathrm{A}^{\mathrm{2}} =\mathrm{A}−−\mathrm{1} \\ $$$$\mathrm{B}^{\mathrm{2}} =\mathrm{B}−−−\mathrm{2} \\ $$$$\mathrm{AB}=\mathrm{BA}−−−\mathrm{3} \\ $$$$\mathrm{for}\:\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{AB} \\ $$$$\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{AB}\bullet\mathrm{AB}=\mathrm{A}\left(\mathrm{BA}\right)\mathrm{B} \\ $$$$\mathrm{from}\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{A}\left(\mathrm{AB}\right)\mathrm{B}=\mathrm{A}^{\mathrm{2}} \mathrm{B}^{\mathrm{2}} \\ $$$$\left(\mathrm{AB}\right)^{\mathrm{2}} =\mathrm{AB}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{from}\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\right\} \\ $$$$\: \\ $$$$\: \\ $$$$\mathrm{check}\:\mathrm{if} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\left(\mathrm{A}+\mathrm{B}\right) \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}^{\mathrm{2}} +\mathrm{AB}+\mathrm{BA}+\mathrm{B}^{\mathrm{2}} =\mathrm{B}+\mathrm{AB}+\mathrm{BA}+\mathrm{B} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}+\mathrm{AB}+\mathrm{BA}+\mathrm{B}=\mathrm{A}+\mathrm{B}+\mathrm{2AB} \\ $$$$\left(\mathrm{A}+\mathrm{B}\right)^{\mathrm{2}} =\mathrm{A}+\mathrm{B}+\mathrm{2AB} \\ $$$$\therefore\:\mathrm{A}+\mathrm{B}\neq\boldsymbol{\mathrm{idempotent}} \\ $$$$\mathrm{since}\:\boldsymbol{\mathrm{AB}}=\boldsymbol{\mathrm{BA}}=\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 10/Feb/25

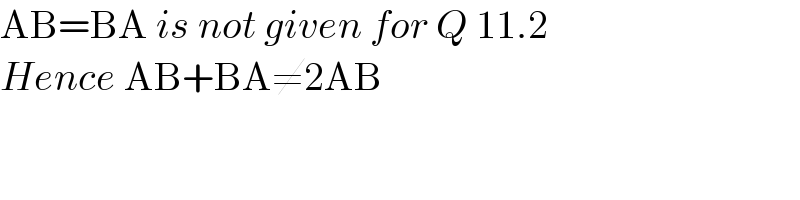
AB=BA is not given for Q 11.2 Hence AB+BA≠2AB

$$\mathrm{AB}=\mathrm{BA}\:{is}\:{not}\:{given}\:{for}\:{Q}\:\mathrm{11}.\mathrm{2} \\ $$$${Hence}\:\mathrm{AB}+\mathrm{BA}\neq\mathrm{2AB} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com