Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 216388 by Tawa11 last updated on 06/Feb/25

Commented by Tawa11 last updated on 06/Feb/25

Q111432

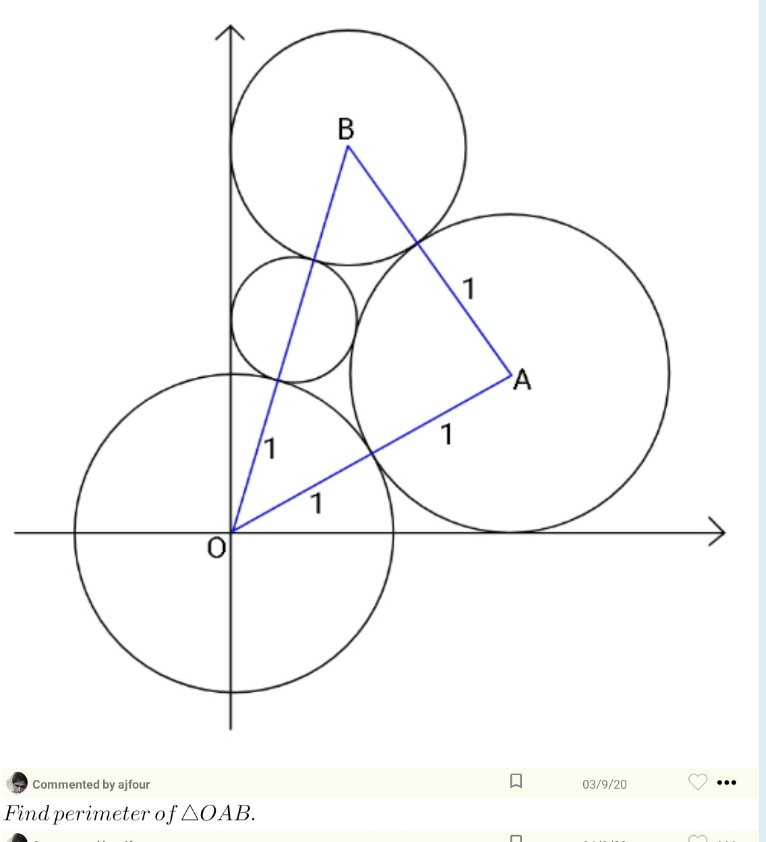
$$\mathrm{Q111432} \\ $$

Answered by mr W last updated on 06/Feb/25

Commented by mr W last updated on 06/Feb/25

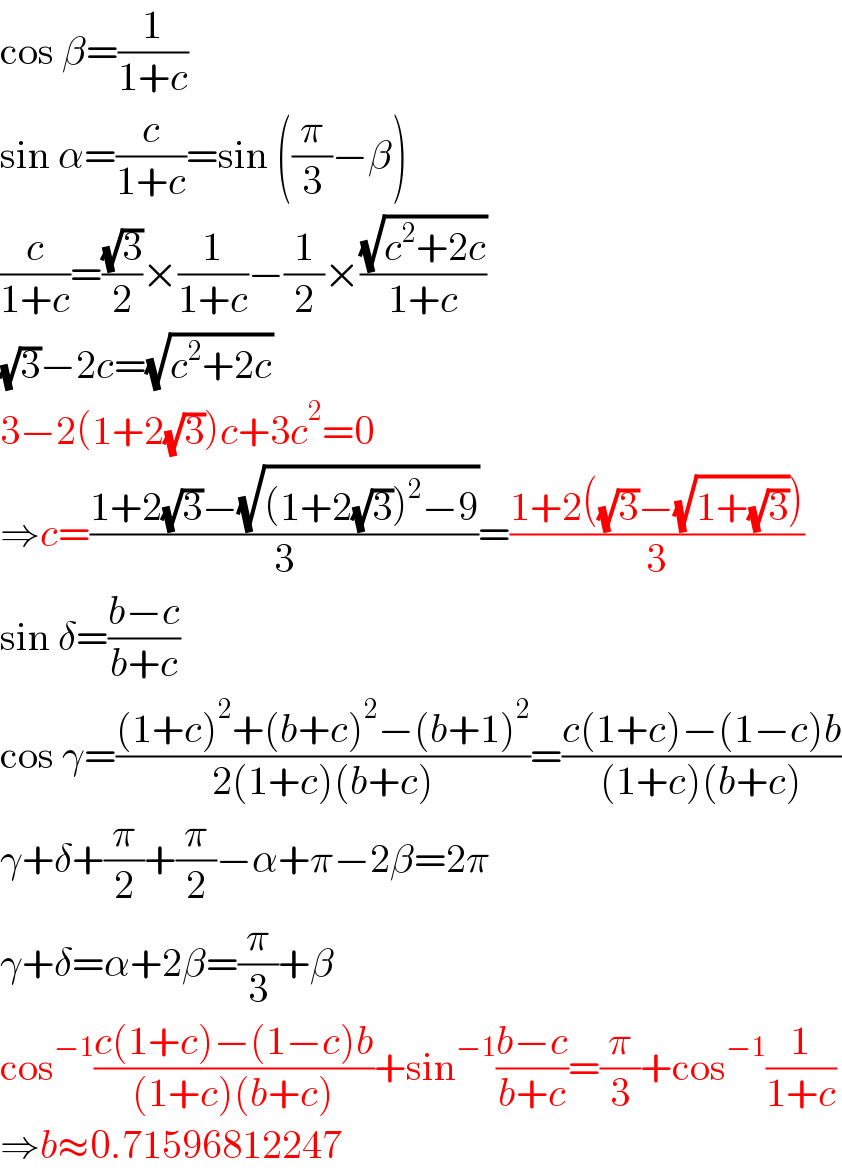
cos β=(1/(1+c)) sin α=(c/(1+c))=sin ((π/3)−β) (c/(1+c))=((√3)/2)×(1/(1+c))−(1/2)×((√(c^2 +2c))/(1+c)) (√3)−2c=(√(c^2 +2c)) 3−2(1+2(√3))c+3c^2 =0 ⇒c=((1+2(√3)−(√((1+2(√3))^2 −9)))/3)=((1+2((√3)−(√(1+(√3)))))/3) sin δ=((b−c)/(b+c)) cos γ=(((1+c)^2 +(b+c)^2 −(b+1)^2 )/(2(1+c)(b+c)))=((c(1+c)−(1−c)b)/((1+c)(b+c))) γ+δ+(π/2)+(π/2)−α+π−2β=2π γ+δ=α+2β=(π/3)+β cos^(−1) ((c(1+c)−(1−c)b)/((1+c)(b+c)))+sin^(−1) ((b−c)/(b+c))=(π/3)+cos^(−1) (1/(1+c)) ⇒b≈0.71596812247

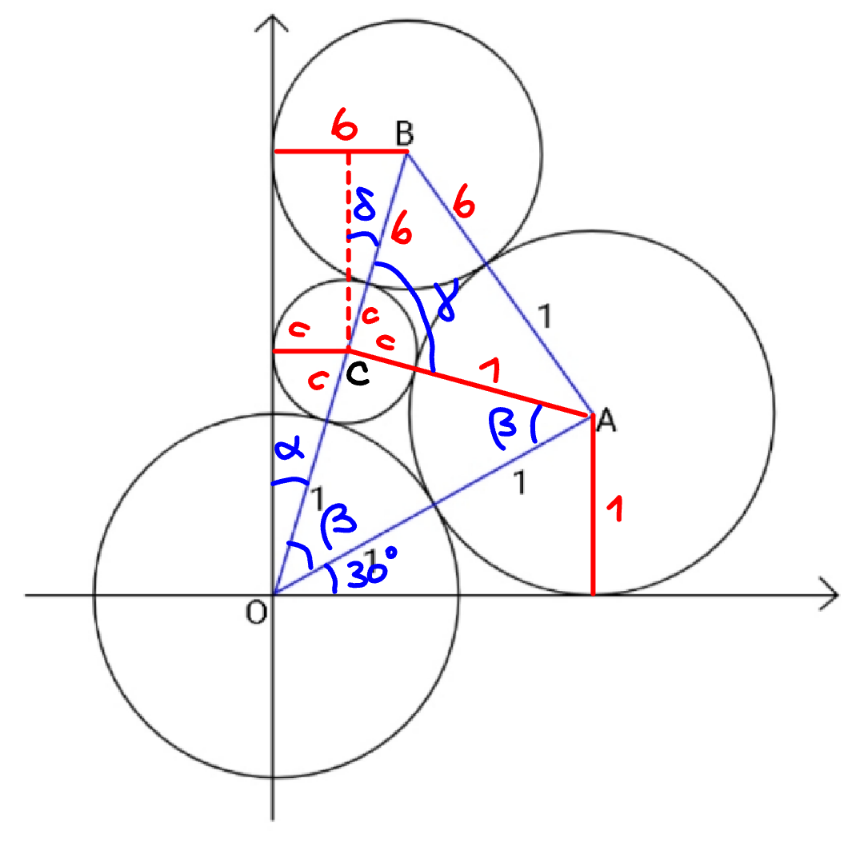
$$\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\mathrm{1}+{c}} \\ $$$$\mathrm{sin}\:\alpha=\frac{{c}}{\mathrm{1}+{c}}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right) \\ $$$$\frac{{c}}{\mathrm{1}+{c}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1}+{c}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{c}^{\mathrm{2}} +\mathrm{2}{c}}}{\mathrm{1}+{c}} \\ $$$$\sqrt{\mathrm{3}}−\mathrm{2}{c}=\sqrt{{c}^{\mathrm{2}} +\mathrm{2}{c}} \\ $$$$\mathrm{3}−\mathrm{2}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right){c}+\mathrm{3}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}=\frac{\mathrm{1}+\mathrm{2}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{1}+\sqrt{\mathrm{3}}}\right)}{\mathrm{3}} \\ $$$$\mathrm{sin}\:\delta=\frac{{b}−{c}}{{b}+{c}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\left(\mathrm{1}+{c}\right)^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} −\left({b}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{c}\right)\left({b}+{c}\right)}=\frac{{c}\left(\mathrm{1}+{c}\right)−\left(\mathrm{1}−{c}\right){b}}{\left(\mathrm{1}+{c}\right)\left({b}+{c}\right)} \\ $$$$\gamma+\delta+\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}−\alpha+\pi−\mathrm{2}\beta=\mathrm{2}\pi \\ $$$$\gamma+\delta=\alpha+\mathrm{2}\beta=\frac{\pi}{\mathrm{3}}+\beta \\ $$$$\mathrm{cos}^{−\mathrm{1}} \frac{{c}\left(\mathrm{1}+{c}\right)−\left(\mathrm{1}−{c}\right){b}}{\left(\mathrm{1}+{c}\right)\left({b}+{c}\right)}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}−{c}}{{b}+{c}}=\frac{\pi}{\mathrm{3}}+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{c}} \\ $$$$\Rightarrow{b}\approx\mathrm{0}.\mathrm{71596812247} \\ $$

Commented by Tawa11 last updated on 06/Feb/25

Great sir. Weldone sir. Thanks sir.

$$\mathrm{Great}\:\mathrm{sir}. \\ $$$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 06/Feb/25

Commented by mr W last updated on 06/Feb/25

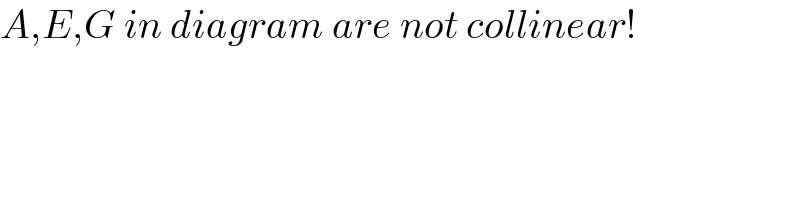
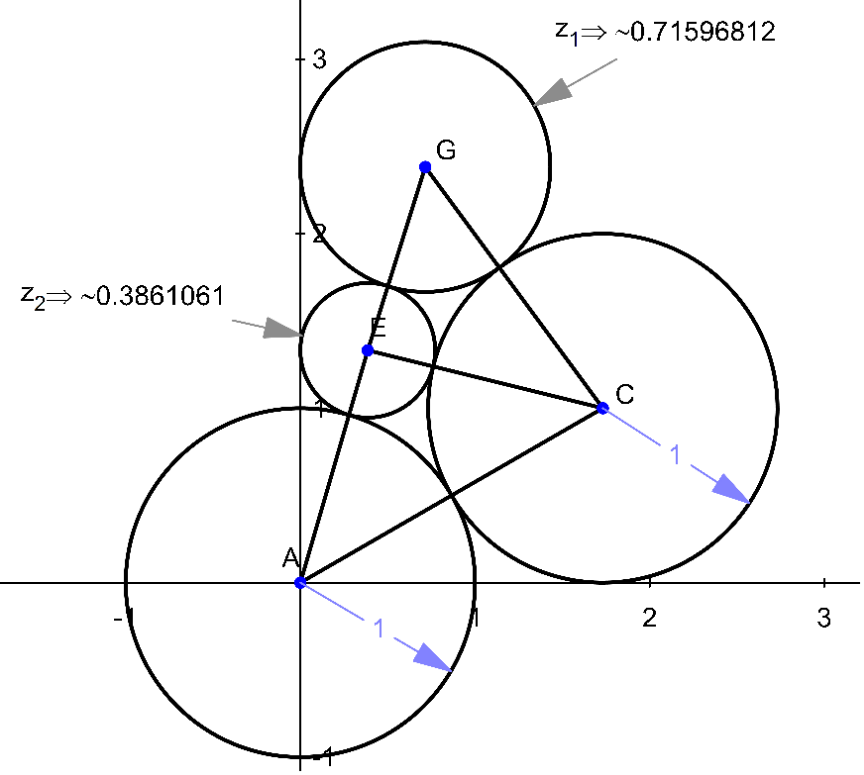
A,E,G in diagram are not collinear!

$${A},{E},{G}\:{in}\:{diagram}\:{are}\:{not}\:{collinear}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com