
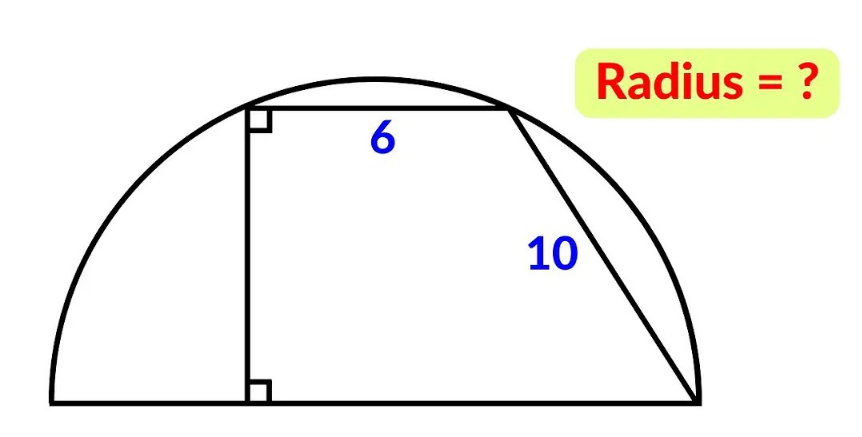
Question Number 216332 by mr W last updated on 04/Feb/25
Answered by cherokeesay last updated on 04/Feb/25
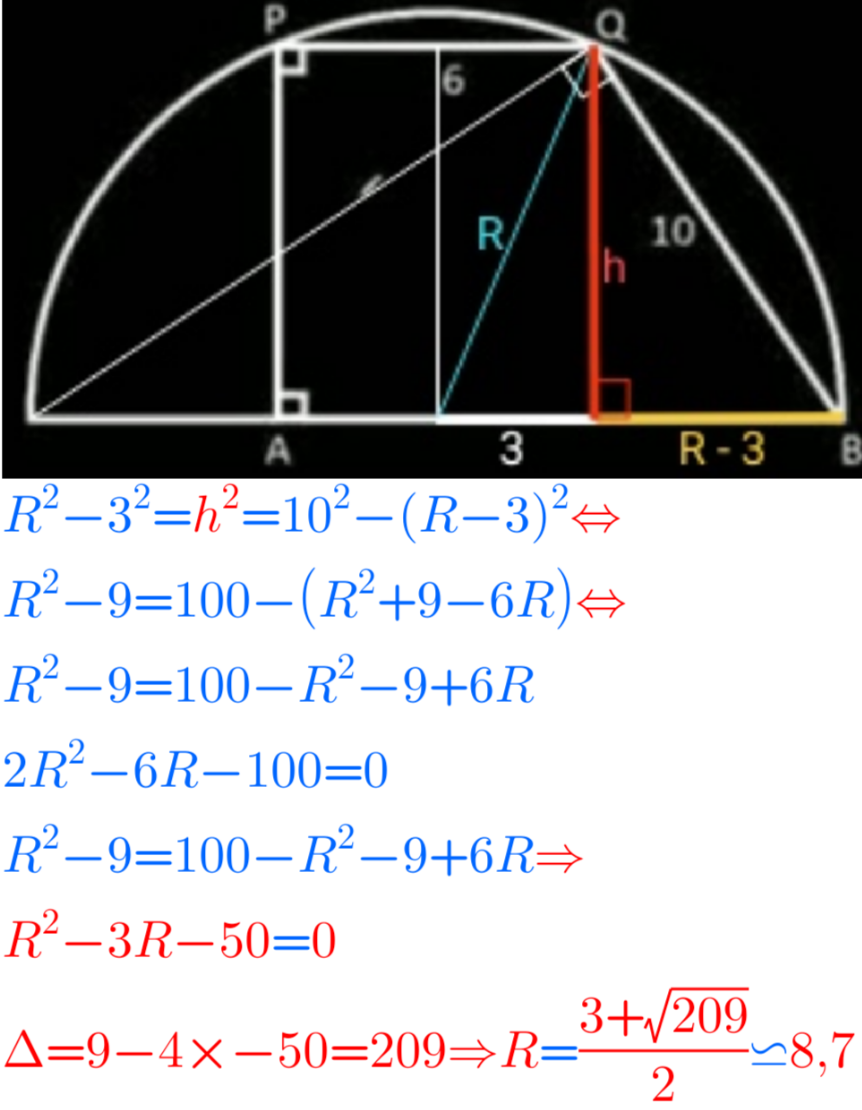
Answered by A5T last updated on 04/Feb/25
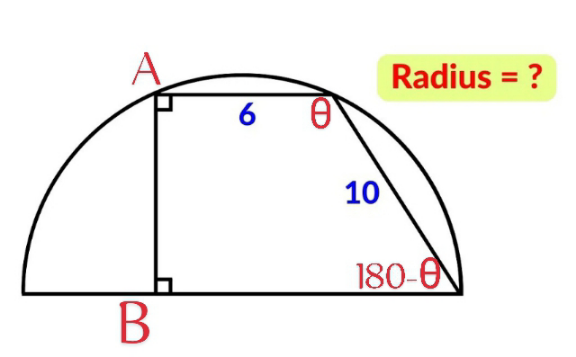
Commented by A5T last updated on 04/Feb/25

$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{6}×\mathrm{10}×\mathrm{sin}\theta=\frac{\mathrm{6}×\mathrm{10}×\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}×\mathrm{6}×\mathrm{10cos}\theta}}{\mathrm{4R}} \\ $$$$\Rightarrow\mathrm{2Rsin}\theta=\sqrt{\mathrm{136}−\mathrm{120cos}\theta}\Rightarrow\mathrm{R}=\frac{\sqrt{\mathrm{34}−\mathrm{30cos}\theta}}{\mathrm{sin}\theta} \\ $$$$\Rightarrow\mathrm{R}^{\mathrm{2}} =\frac{\mathrm{34}−\mathrm{30cos}\theta}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}...\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{sin}\left(\mathrm{180}−\theta\right)}{\mathrm{AB}}=\frac{\mathrm{sin90}}{\mathrm{10}}\Rightarrow\mathrm{AB}=\mathrm{10sin}\theta \\ $$$$\left(\mathrm{2R}\right)^{\mathrm{2}} =\left(\mathrm{2AB}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{R}^{\mathrm{2}} =\mathrm{100sin}^{\mathrm{2}} \theta+\mathrm{9}=\mathrm{109}−\mathrm{100cos}^{\mathrm{2}} \theta...\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\&\left(\mathrm{ii}\right)\Rightarrow\mathrm{109}−\mathrm{100cos}^{\mathrm{2}} \theta=\frac{\mathrm{34}−\mathrm{30cos}\theta}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\mathrm{cos}\theta=\frac{\mathrm{3}\underset{−} {+}\sqrt{\mathrm{209}}}{\mathrm{20}} \\ $$$$\Rightarrow\mathrm{R}^{\mathrm{2}} =\mathrm{109}−\frac{\mathrm{109}\underset{−} {+}\mathrm{3}\sqrt{\mathrm{209}}}{\mathrm{2}}=\frac{\mathrm{109}\overset{−} {+}\mathrm{3}\sqrt{\mathrm{209}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{R}=\sqrt{\frac{\mathrm{109}+\mathrm{3}\sqrt{\mathrm{209}}}{\mathrm{2}}}=\frac{\mathrm{3}+\sqrt{\mathrm{209}}}{\mathrm{2}}\approx\mathrm{8}.\mathrm{728} \\ $$
Commented by mahdipoor last updated on 04/Feb/25
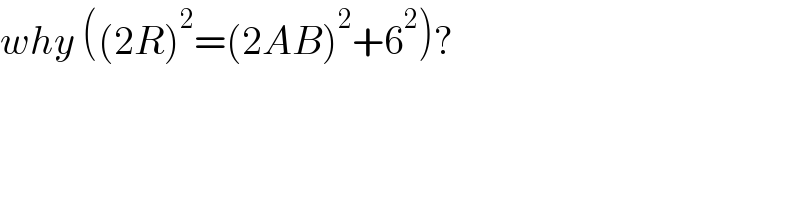
$${why}\:\left(\left(\mathrm{2}{R}\right)^{\mathrm{2}} =\left(\mathrm{2}{AB}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \right)? \\ $$$$ \\ $$
Commented by A5T last updated on 04/Feb/25

$$\mathrm{The}\:\mathrm{diameter},\:\mathrm{length}\:\mathrm{2R},\:\mathrm{subtends}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of} \\ $$$$\mathrm{90}°\:\mathrm{at}\:\mathrm{the}\:\mathrm{circumference}. \\ $$
Commented by A5T last updated on 04/Feb/25
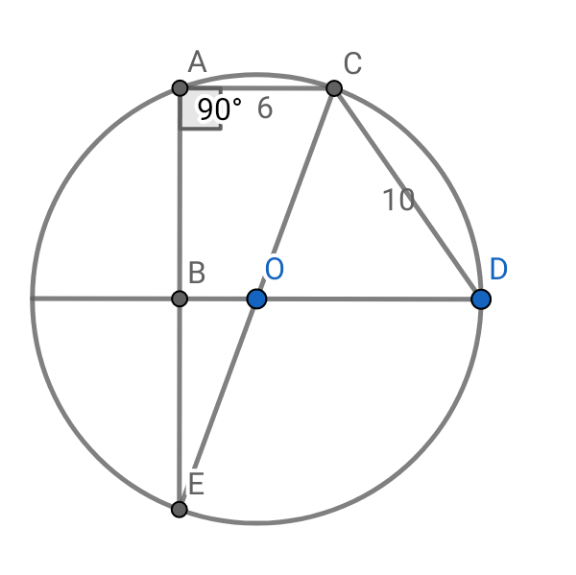
Commented by A5T last updated on 04/Feb/25
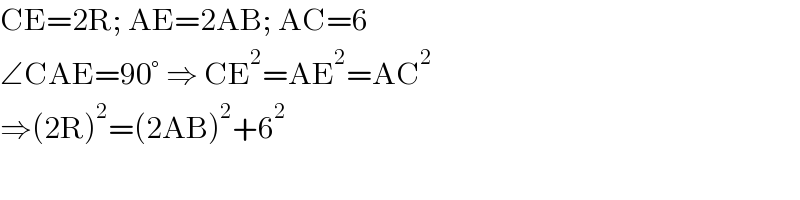
$$\mathrm{CE}=\mathrm{2R};\:\mathrm{AE}=\mathrm{2AB};\:\mathrm{AC}=\mathrm{6} \\ $$$$\angle\mathrm{CAE}=\mathrm{90}°\:\Rightarrow\:\mathrm{CE}^{\mathrm{2}} =\mathrm{AE}^{\mathrm{2}} =\mathrm{AC}^{\mathrm{2}} \: \\ $$$$\Rightarrow\left(\mathrm{2R}\right)^{\mathrm{2}} =\left(\mathrm{2AB}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 04/Feb/25
��
Answered by mr W last updated on 04/Feb/25
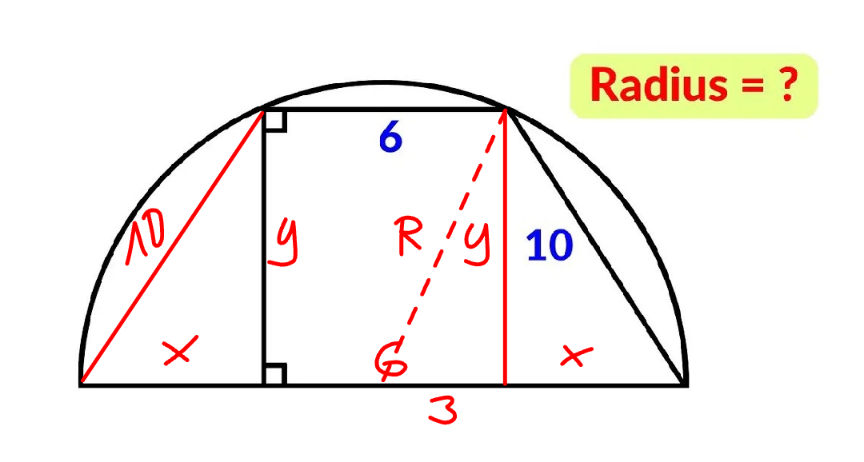
Commented by mr W last updated on 04/Feb/25
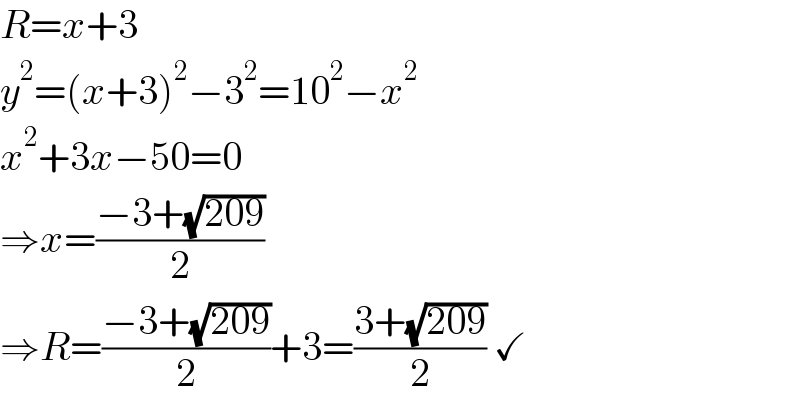
$${R}={x}+\mathrm{3} \\ $$$${y}^{\mathrm{2}} =\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{50}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{3}+\sqrt{\mathrm{209}}}{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{−\mathrm{3}+\sqrt{\mathrm{209}}}{\mathrm{2}}+\mathrm{3}=\frac{\mathrm{3}+\sqrt{\mathrm{209}}}{\mathrm{2}}\:\checkmark \\ $$
Answered by A5T last updated on 05/Feb/25
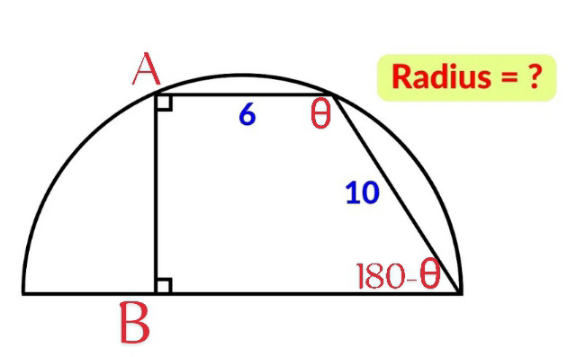
Commented by A5T last updated on 05/Feb/25
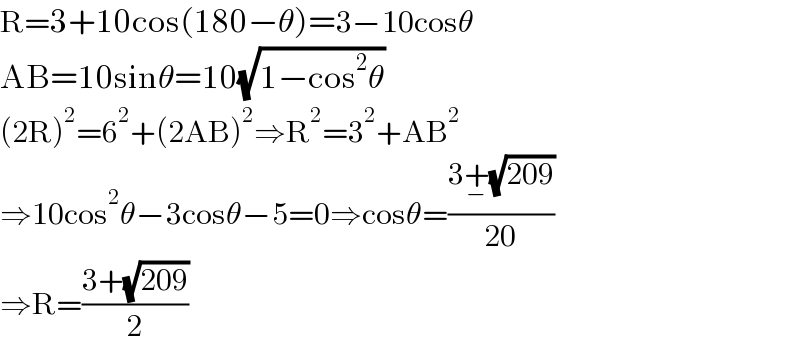
$$\mathrm{R}=\mathrm{3}+\mathrm{10cos}\left(\mathrm{180}−\theta\right)=\mathrm{3}−\mathrm{10cos}\theta \\ $$$$\mathrm{AB}=\mathrm{10sin}\theta=\mathrm{10}\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$\left(\mathrm{2R}\right)^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +\left(\mathrm{2AB}\right)^{\mathrm{2}} \Rightarrow\mathrm{R}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +\mathrm{AB}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{10cos}^{\mathrm{2}} \theta−\mathrm{3cos}\theta−\mathrm{5}=\mathrm{0}\Rightarrow\mathrm{cos}\theta=\frac{\mathrm{3}\underset{−} {+}\sqrt{\mathrm{209}}}{\mathrm{20}} \\ $$$$\Rightarrow\mathrm{R}=\frac{\mathrm{3}+\sqrt{\mathrm{209}}}{\mathrm{2}} \\ $$
