
Question Number 216324 by Jubr last updated on 04/Feb/25

Commented by Jubr last updated on 04/Feb/25
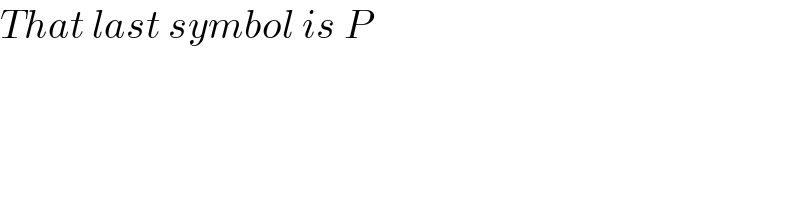
$${That}\:{last}\:{symbol}\:{is}\:{P} \\ $$
Answered by mr W last updated on 04/Feb/25

$${T}=\mathrm{5}{mg} \\ $$$${l}_{\mathrm{0}} =\mathrm{5}{a} \\ $$$$\Delta{l}=\frac{{l}_{\mathrm{0}} }{\mathrm{8}{mg}}×\mathrm{5}{mg}=\frac{\mathrm{5}{l}_{\mathrm{0}} }{\mathrm{8}}=\frac{\mathrm{25}{a}}{\mathrm{8}} \\ $$$${l}=\mathrm{5}{a}+\frac{\mathrm{25}{a}}{\mathrm{8}}=\frac{\mathrm{65}{a}}{\mathrm{8}} \\ $$$${SP}={b}={l}−\mathrm{2}{a}=\frac{\mathrm{49}{a}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{3}{mg}}{{T}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${r}={b}\:\mathrm{cos}\:\theta=\frac{\mathrm{49}{a}}{\mathrm{8}}×\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{49}{a}}{\mathrm{10}} \\ $$$$\mathrm{3}{m}\omega^{\mathrm{2}} {r}={T}\:\mathrm{cos}\:\theta=\mathrm{5}{mg}×\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{3}\omega^{\mathrm{2}} ×\frac{\mathrm{49}{a}}{\mathrm{10}}=\mathrm{4}{g} \\ $$$$\Rightarrow\omega=\frac{\mathrm{2}}{\mathrm{21}}\sqrt{\frac{\mathrm{30}{g}}{{a}}} \\ $$
Commented by Jubr last updated on 04/Feb/25

$${Thanks}\:{sir}. \\ $$
Commented by mr W last updated on 06/Feb/25

$${Q}\:{remains}\:{stationary},\:{that}\:{means} \\ $$$${it}\:{doesn}'{t}\:{move}\:{at}\:{all}.\:{its}\:{velocity} \\ $$$${and}\:{angular}\:{velocity}\:{are}\:{zero}! \\ $$$${but}\:{it}\:{rotates}\:{about}\:{its}\:{axis}\:{with} \\ $$$$\omega. \\ $$
Commented by Jubr last updated on 06/Feb/25
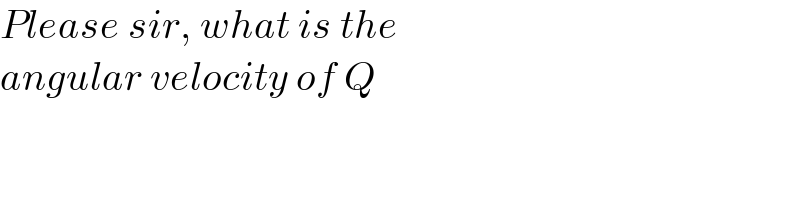
$${Please}\:{sir},\:{what}\:{is}\:{the} \\ $$$${angular}\:{velocity}\:{of}\:{Q} \\ $$
Commented by Jubr last updated on 10/Feb/25

$${Thanks}\:{sir}. \\ $$
