Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 216245 by Tawa11 last updated on 01/Feb/25

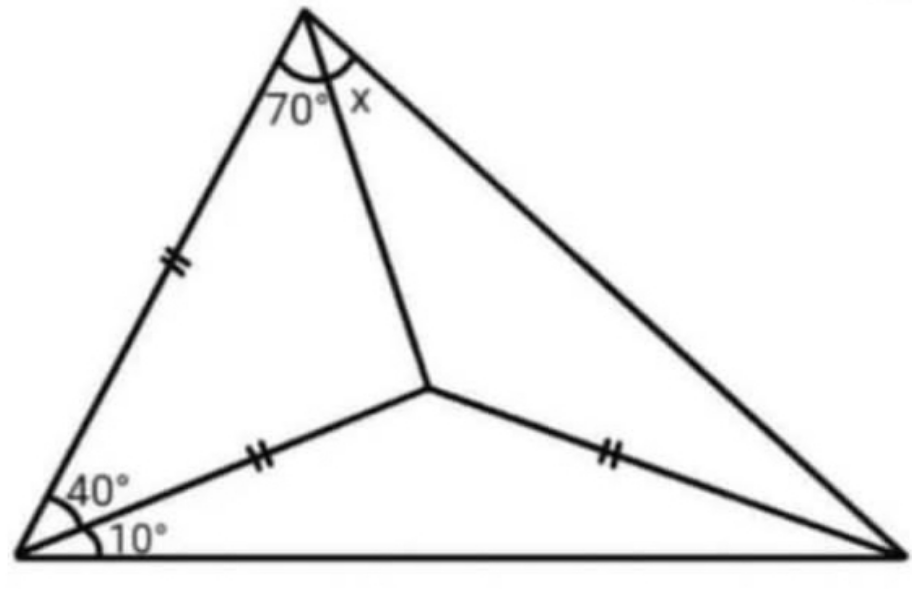
Commented by Tawa11 last updated on 01/Feb/25

I can use cosine rule. But I want to see if there is better approach.

$$\mathrm{I}\:\mathrm{can}\:\mathrm{use}\:\mathrm{cosine}\:\mathrm{rule}. \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{see}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is} \\ $$$$\mathrm{better}\:\mathrm{approach}. \\ $$

Commented by Tawa11 last updated on 01/Feb/25

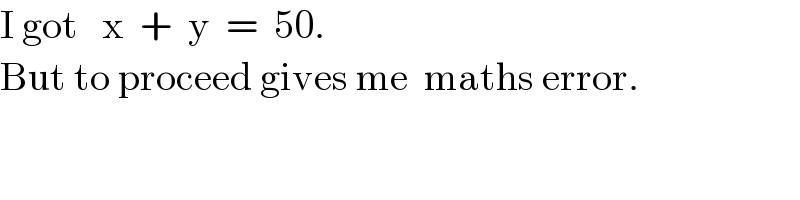
I got x + y = 50. But to proceed gives me maths error.

$$\mathrm{I}\:\mathrm{got}\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{50}. \\ $$$$\mathrm{But}\:\mathrm{to}\:\mathrm{proceed}\:\mathrm{gives}\:\mathrm{me}\:\:\mathrm{maths}\:\mathrm{error}. \\ $$

Commented by mr W last updated on 02/Feb/25

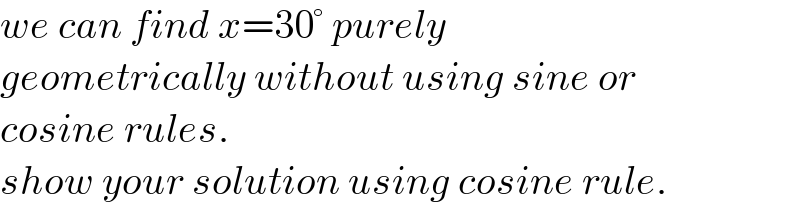
we can find x=30° purely geometrically without using sine or cosine rules. show your solution using cosine rule.

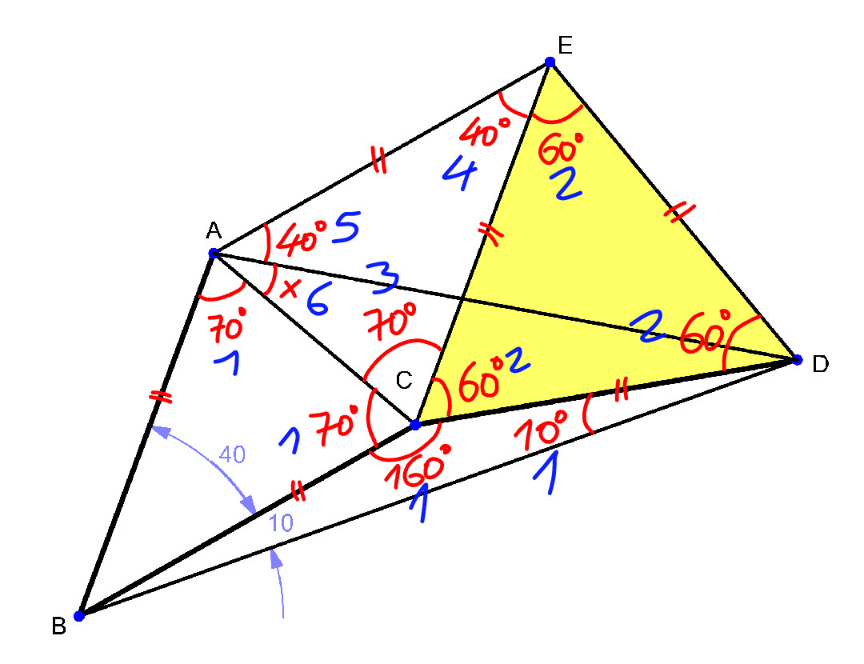
$${we}\:{can}\:{find}\:{x}=\mathrm{30}°\:{purely} \\ $$$${geometrically}\:{without}\:{using}\:{sine}\:{or}\: \\ $$$${cosine}\:{rules}. \\ $$$${show}\:{your}\:{solution}\:{using}\:{cosine}\:{rule}. \\ $$

Commented by Tawa11 last updated on 01/Feb/25

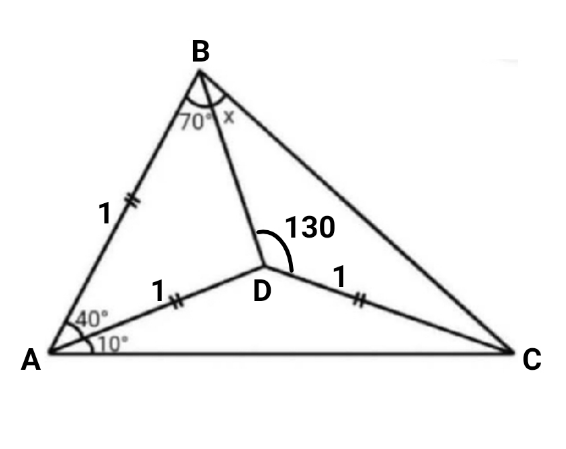
Commented by Tawa11 last updated on 01/Feb/25

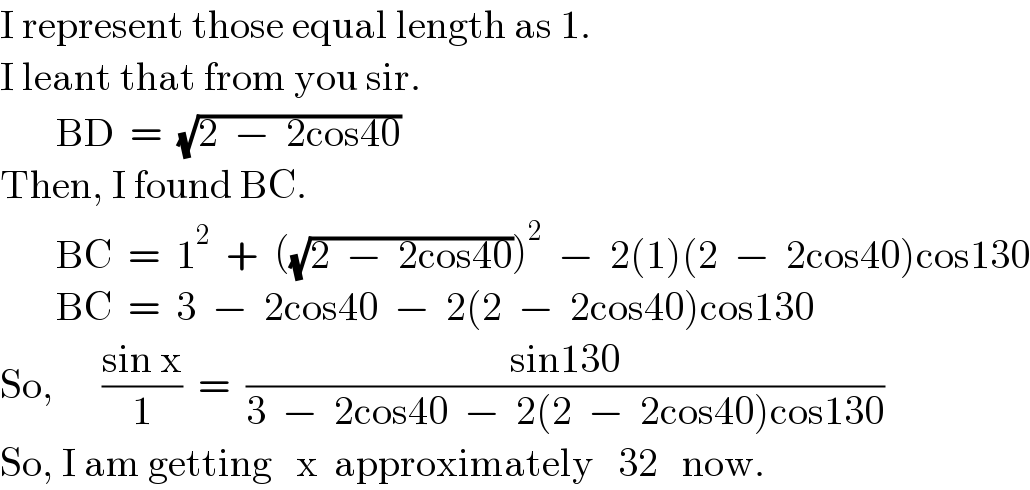
I represent those equal length as 1. I leant that from you sir. BD = (√(2 − 2cos40)) Then, I found BC. BC = 1^2 + ((√(2 − 2cos40)))^2 − 2(1)(2 − 2cos40)cos130 BC = 3 − 2cos40 − 2(2 − 2cos40)cos130 So, ((sin x)/1) = ((sin130)/(3 − 2cos40 − 2(2 − 2cos40)cos130)) So, I am getting x approximately 32 now.

$$\mathrm{I}\:\mathrm{represent}\:\mathrm{those}\:\mathrm{equal}\:\mathrm{length}\:\mathrm{as}\:\mathrm{1}. \\ $$$$\mathrm{I}\:\mathrm{leant}\:\mathrm{that}\:\mathrm{from}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\:\:\:\:\:\:\:\mathrm{BD}\:\:=\:\:\sqrt{\mathrm{2}\:\:−\:\:\mathrm{2cos40}} \\ $$$$\mathrm{Then},\:\mathrm{I}\:\mathrm{found}\:\mathrm{BC}. \\ $$$$\:\:\:\:\:\:\:\mathrm{BC}\:\:=\:\:\mathrm{1}^{\mathrm{2}} \:\:+\:\:\left(\sqrt{\mathrm{2}\:\:−\:\:\mathrm{2cos40}}\right)^{\mathrm{2}} \:\:−\:\:\mathrm{2}\left(\mathrm{1}\right)\left(\mathrm{2}\:\:−\:\:\mathrm{2cos40}\right)\mathrm{cos130} \\ $$$$\:\:\:\:\:\:\:\mathrm{BC}\:\:=\:\:\mathrm{3}\:\:−\:\:\mathrm{2cos40}\:\:−\:\:\mathrm{2}\left(\mathrm{2}\:\:−\:\:\mathrm{2cos40}\right)\mathrm{cos130} \\ $$$$\mathrm{So},\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}}\:\:=\:\:\frac{\mathrm{sin130}}{\mathrm{3}\:\:−\:\:\mathrm{2cos40}\:\:−\:\:\mathrm{2}\left(\mathrm{2}\:\:−\:\:\mathrm{2cos40}\right)\mathrm{cos130}} \\ $$$$\mathrm{So},\:\mathrm{I}\:\mathrm{am}\:\mathrm{getting}\:\:\:\mathrm{x}\:\:\mathrm{approximately}\:\:\:\mathrm{32}\:\:\:\mathrm{now}. \\ $$

Commented by mr W last updated on 02/Feb/25

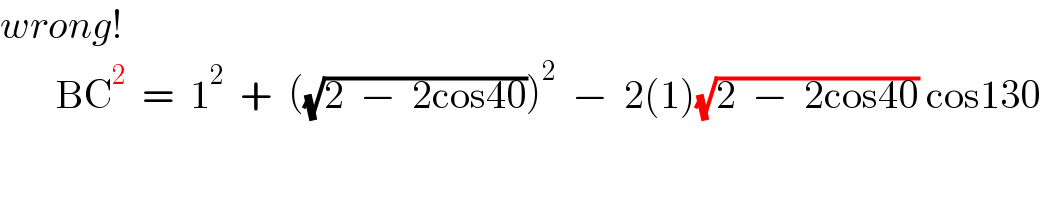
wrong! BC^2 = 1^2 + ((√(2 − 2cos40)))^2 − 2(1)(√(2 − 2cos40)) cos130

$${wrong}! \\ $$$$\:\:\:\:\:\:\:\mathrm{BC}^{\mathrm{2}} \:\:=\:\:\mathrm{1}^{\mathrm{2}} \:\:+\:\:\left(\sqrt{\mathrm{2}\:\:−\:\:\mathrm{2cos40}}\right)^{\mathrm{2}} \:\:−\:\:\mathrm{2}\left(\mathrm{1}\right)\sqrt{\mathrm{2}\:\:−\:\:\mathrm{2cos40}}\:\mathrm{cos130} \\ $$

Commented by Tawa11 last updated on 02/Feb/25

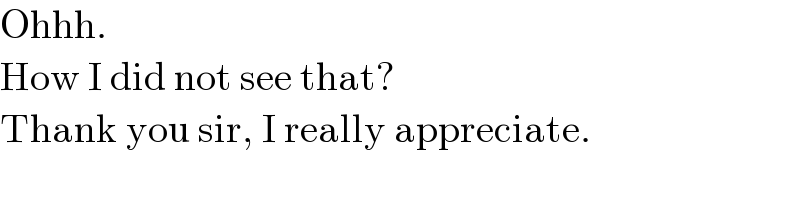
Ohhh. How I did not see that? Thank you sir, I really appreciate.

$$\mathrm{Ohhh}. \\ $$$$\mathrm{How}\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{see}\:\mathrm{that}? \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Answered by mr W last updated on 01/Feb/25

Commented by mr W last updated on 02/Feb/25

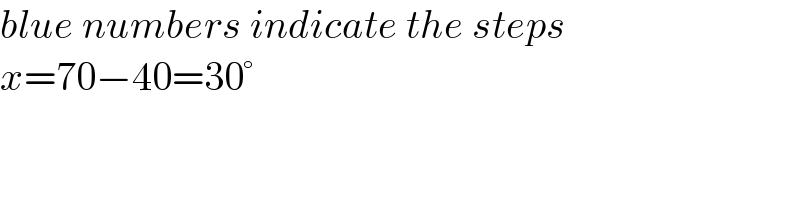
blue numbers indicate the steps x=70−40=30°

$${blue}\:{numbers}\:{indicate}\:{the}\:{steps} \\ $$$${x}=\mathrm{70}−\mathrm{40}=\mathrm{30}° \\ $$

Commented by Tawa11 last updated on 02/Feb/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by ArshadS last updated on 02/Feb/25

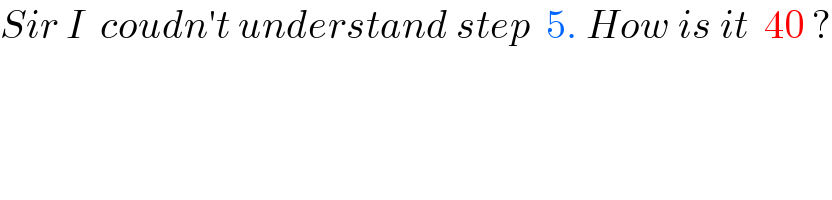
Sir I coudn′t understand step 5. How is it 40 ?

$${Sir}\:{I}\:\:{coudn}'{t}\:{understand}\:{step}\:\:\mathrm{5}.\:{How}\:{is}\:{it}\:\:\mathrm{40}\:? \\ $$

Commented by mr W last updated on 02/Feb/25

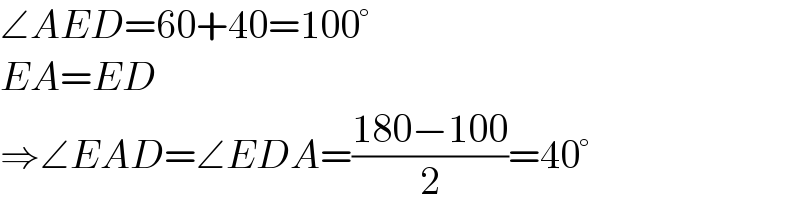
∠AED=60+40=100° EA=ED ⇒∠EAD=∠EDA=((180−100)/2)=40°

$$\angle{AED}=\mathrm{60}+\mathrm{40}=\mathrm{100}° \\ $$$${EA}={ED}\: \\ $$$$\Rightarrow\angle{EAD}=\angle{EDA}=\frac{\mathrm{180}−\mathrm{100}}{\mathrm{2}}=\mathrm{40}° \\ $$

Commented by ArshadS last updated on 03/Feb/25

Thanks Sir! I understood now.

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\mathbb{S}\boldsymbol{\mathrm{ir}}!\:\mathrm{I}\:\mathrm{understood}\:\mathrm{now}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com