
Question Number 216219 by mr W last updated on 30/Jan/25
Commented by mr W last updated on 31/Jan/25

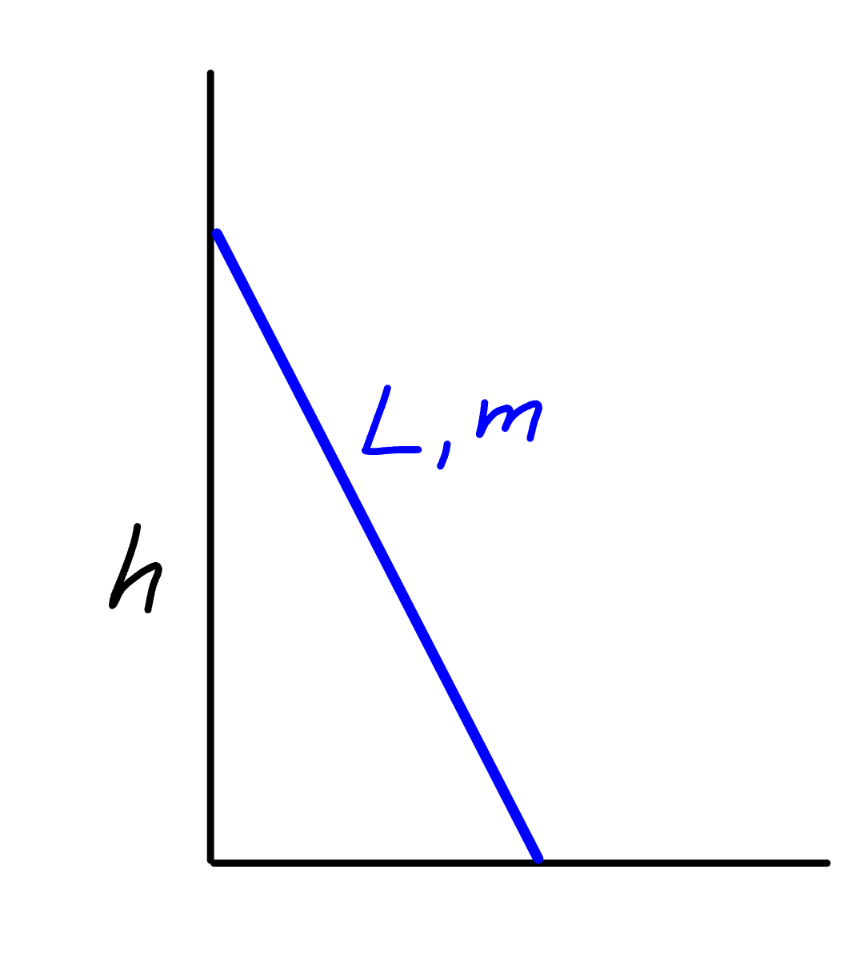
$${a}\:{ladder}\:{with}\:{length}\:{L}\:{and}\:{mass}\:{m} \\ $$$${is}\:{released}\:{from}\:{rest}\:{at}\:{the}\:{position} \\ $$$${as}\:{shown}.\:{find}\:{the}\:{time}\:{the}\:{ladder} \\ $$$${takes}\:{to}\:{fall}\:{onto}\:{the}\:{floor}\:{completely}. \\ $$$${all}\:{surfaces}\:{are}\:{frictionless}. \\ $$
Answered by mahdipoor last updated on 01/Feb/25
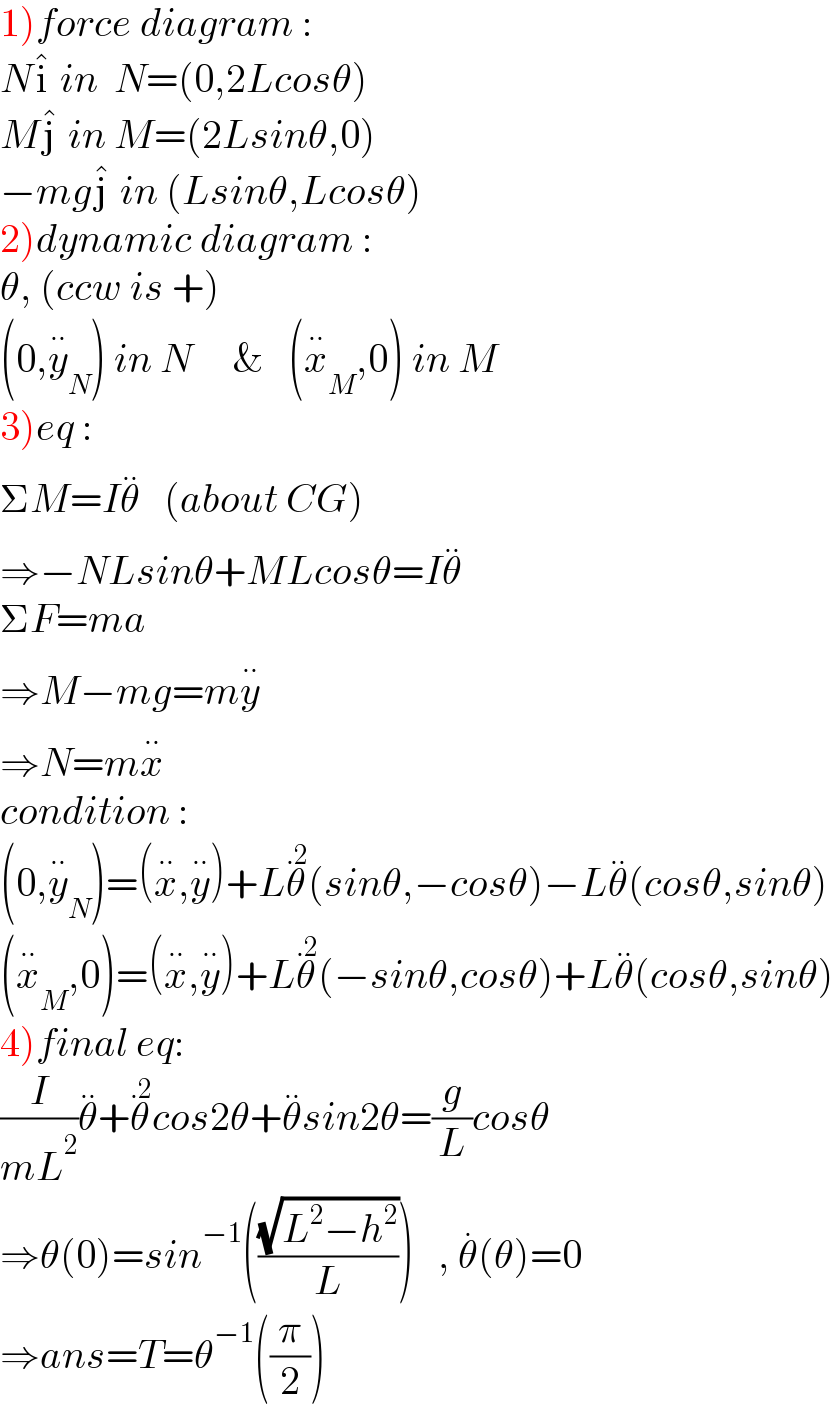
$$\left.\mathrm{1}\right){force}\:{diagram}\:: \\ $$$${N}\hat {\mathrm{i}}\:{in}\:\:{N}=\left(\mathrm{0},\mathrm{2}{Lcos}\theta\right) \\ $$$${M}\hat {\mathrm{j}}\:{in}\:{M}=\left(\mathrm{2}{Lsin}\theta,\mathrm{0}\right) \\ $$$$−{mg}\hat {\mathrm{j}}\:{in}\:\left({Lsin}\theta,{Lcos}\theta\right) \\ $$$$\left.\mathrm{2}\right){dynamic}\:{diagram}\:: \\ $$$$\theta,\:\left({ccw}\:{is}\:+\right) \\ $$$$\left(\mathrm{0},\overset{..} {{y}}_{{N}} \right)\:{in}\:{N}\:\:\:\:\:\&\:\:\:\left(\overset{..} {{x}}_{{M}} ,\mathrm{0}\right)\:{in}\:{M} \\ $$$$\left.\mathrm{3}\right){eq}\:: \\ $$$$\Sigma{M}={I}\overset{..} {\theta}\:\:\:\left({about}\:{CG}\right) \\ $$$$\Rightarrow−{NLsin}\theta+{MLcos}\theta={I}\overset{..} {\theta} \\ $$$$\Sigma{F}={ma}\: \\ $$$$\Rightarrow{M}−{mg}={m}\overset{..} {{y}} \\ $$$$\Rightarrow{N}={m}\overset{..} {{x}} \\ $$$${condition}\:: \\ $$$$\left(\mathrm{0},\overset{..} {{y}}_{{N}} \right)=\left(\overset{..} {{x}},\overset{..} {{y}}\right)+{L}\overset{.\mathrm{2}} {\theta}\left({sin}\theta,−{cos}\theta\right)−{L}\overset{..} {\theta}\left({cos}\theta,{sin}\theta\right) \\ $$$$\left(\overset{..} {{x}}_{{M}} ,\mathrm{0}\right)=\left(\overset{..} {{x}},\overset{..} {{y}}\right)+{L}\overset{.\mathrm{2}} {\theta}\left(−{sin}\theta,{cos}\theta\right)+{L}\overset{..} {\theta}\left({cos}\theta,{sin}\theta\right) \\ $$$$\left.\mathrm{4}\right){final}\:{eq}: \\ $$$$\frac{{I}}{{mL}^{\mathrm{2}} }\overset{..} {\theta}+\overset{.\mathrm{2}} {\theta}{cos}\mathrm{2}\theta+\overset{..} {\theta}{sin}\mathrm{2}\theta=\frac{{g}}{{L}}{cos}\theta \\ $$$$\Rightarrow\theta\left(\mathrm{0}\right)={sin}^{−\mathrm{1}} \left(\frac{\sqrt{{L}^{\mathrm{2}} −{h}^{\mathrm{2}} }}{{L}}\right)\:\:\:,\:\overset{.} {\theta}\left(\theta\right)=\mathrm{0} \\ $$$$\Rightarrow{ans}={T}=\theta^{−\mathrm{1}} \left(\frac{\pi}{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 01/Feb/25

$${thanks}! \\ $$
Answered by mr W last updated on 01/Feb/25
Commented by mr W last updated on 05/Feb/25
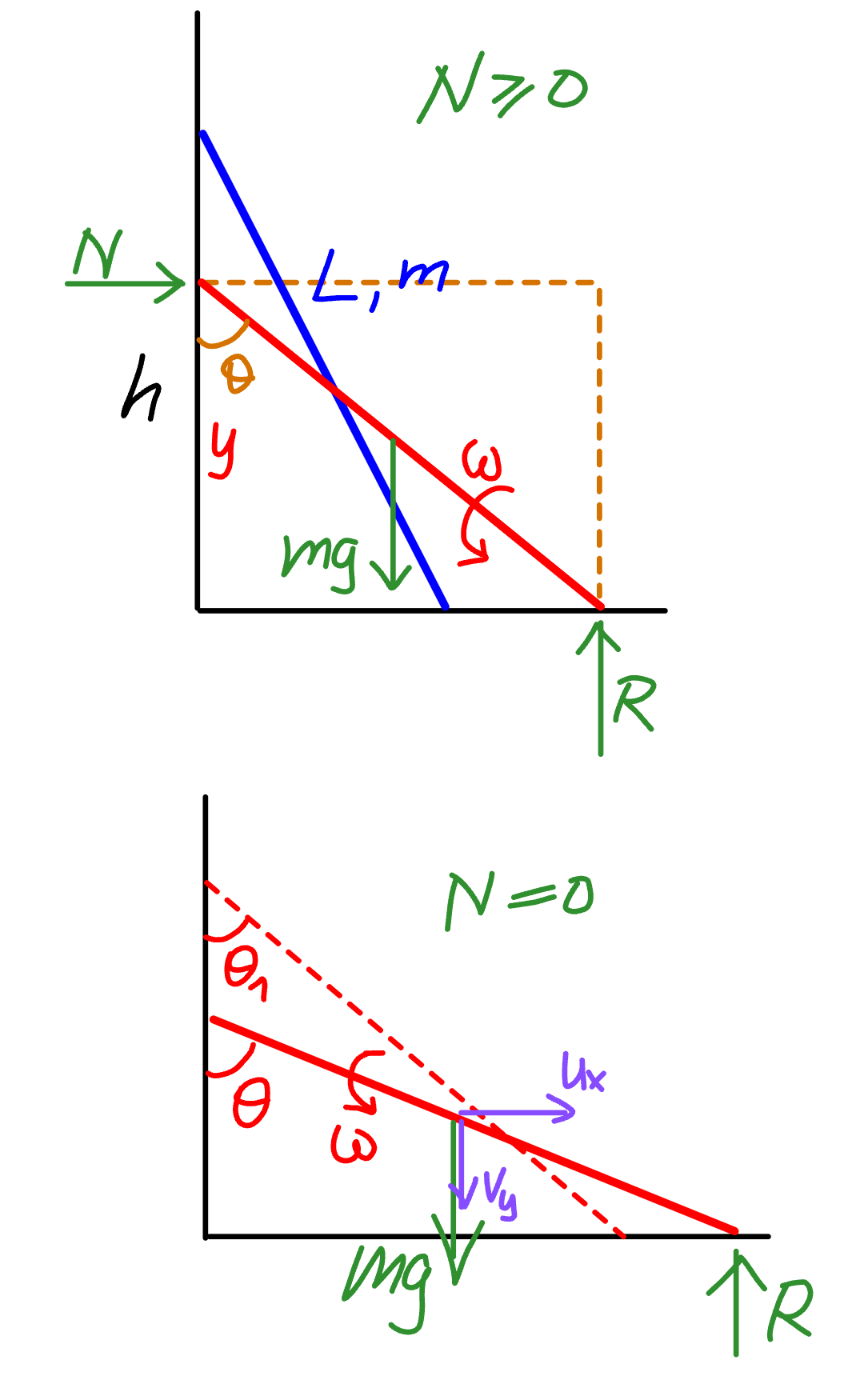
![let (h/L)=η ω=(dθ/dt) y=L cos θ at t=0: y=h=L cos θ_0 ⇒θ_0 =cos^(−1) η (1/2)[((mL^2 )/(12))+m((L/2))^2 ]ω^2 =((mg(h−y))/2) ((L^2 ω^2 )/3)=g(h−L cos θ) ω^2 =((3g)/L)(η−cos θ) ⇒ω(dω/dθ)=((3g)/(2L)) sin θ ⇒ω=(√(((3g)/L)(η−cos θ))) u_x =((Lω cos θ)/2) a_x =(L/2)(−ω^2 sin θ+cos θ ((ωdω)/dθ)) =(L/2)[−((3g)/L)(η−cos θ) sin θ+cos θ ((3g)/(2L)) sin θ] =((3g)/4)(−2η+3 cos θ)sin θ N=ma_x =((3mg)/4)(−2η+3 cos θ)sin θ N=0: ⇒−2η+3 cos θ=0 ⇒cos θ=((2η)/3) ⇒θ_1 =cos^(−1) ((2η)/3) dt=(√(L/(3g)))(dθ/( (√(η−cos θ)))) ∫_0 ^T_1 dt=(√(L/(3g)))∫_θ_0 ^θ_1 (dθ/( (√(η−cos θ)))) ⇒T_1 =(√(L/(3g)))∫_(cos^(−1) η) ^(cos^(−1) ((2η)/3)) (dθ/( (√(η−cos θ)))) ω_1 =(√(((3g)/L)(η−cos θ_1 ))) u_1 =u_x ∣_(t=T_1 ) =((Lω_1 cos θ_1 )/2)=((cos θ_1 )/2)(√(3gL(η−cos θ_1 ))) upon t=T_1 : u_x =u_1 =((cos θ_1 )/2)(√(3gL(η−cos θ_1 )))=(η/3)(√(ηgL)) v_y =((Lω sin θ)/2) (1/2)×((mL^2 ω^2 )/(12))+((m(u_x ^2 +v_y ^2 ))/2)=((mg(h−y))/2) (1/2)×((mL^2 ω^2 )/(12))+(m/2)×(((η^3 gL)/9)+((L^2 ω^2 sin^2 θ)/4))=((mg(h−L cos θ))/2) ⇒ω=(√((12g(η−(η^3 /9)−cos θ))/(L(1+3 sin^2 θ)))) (dθ/dt)=(√((12g(η−(η^3 /9)−cos θ))/(L(1+3 sin^2 θ)))) dt=(√((L(1+3 sin^2 θ))/(12g(η−(η^3 /9)−cos θ)))) dθ ∫_0 ^T_2 dt=(√(L/(3g)))∫_θ_1 ^(π/2) (√((1+3 sin^2 θ)/(4(η−(η^3 /9)−cos θ)))) dθ ⇒T_2 =(√(L/(3g)))∫_(cos^(−1) ((2η)/3)) ^(π/2) (√((1+3 sin^2 θ)/(4(η−(η^3 /9)−cos θ)))) dθ total time needed: T=T_1 +T_2 =λ(√(L/(3g))) with λ=∫_(cos^(−1) η) ^(cos^(−1) ((2η)/3)) (dθ/( (√(η−cos θ))))+∫_(cos^(−1) ((2η)/3)) ^(π/2) (√((1+3 sin^2 θ)/(4(η−(η^3 /9)−cos θ)))) dθ example: η=(h/L)=0.8 To≈1.73205081(√(L/g))](Q216238.png)
$${let}\:\frac{{h}}{{L}}=\eta \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${y}={L}\:\mathrm{cos}\:\theta \\ $$$${at}\:{t}=\mathrm{0}:\: \\ $$$${y}={h}={L}\:\mathrm{cos}\:\theta_{\mathrm{0}} \:\Rightarrow\theta_{\mathrm{0}} =\mathrm{cos}^{−\mathrm{1}} \eta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}+{m}\left(\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} \right]\omega^{\mathrm{2}} =\frac{{mg}\left({h}−{y}\right)}{\mathrm{2}} \\ $$$$\frac{{L}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{3}}={g}\left({h}−{L}\:\mathrm{cos}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{3}{g}}{{L}}\left(\eta−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\omega\frac{{d}\omega}{{d}\theta}=\frac{\mathrm{3}{g}}{\mathrm{2}{L}}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{3}{g}}{{L}}\left(\eta−\mathrm{cos}\:\theta\right)} \\ $$$${u}_{{x}} =\frac{{L}\omega\:\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$${a}_{{x}} =\frac{{L}}{\mathrm{2}}\left(−\omega^{\mathrm{2}} \:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\frac{\omega{d}\omega}{{d}\theta}\right) \\ $$$$\:\:\:\:=\frac{{L}}{\mathrm{2}}\left[−\frac{\mathrm{3}{g}}{{L}}\left(\eta−\mathrm{cos}\:\theta\right)\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\frac{\mathrm{3}{g}}{\mathrm{2}{L}}\:\mathrm{sin}\:\theta\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}{g}}{\mathrm{4}}\left(−\mathrm{2}\eta+\mathrm{3}\:\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta \\ $$$${N}={ma}_{{x}} =\frac{\mathrm{3}{mg}}{\mathrm{4}}\left(−\mathrm{2}\eta+\mathrm{3}\:\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta \\ $$$${N}=\mathrm{0}: \\ $$$$\Rightarrow−\mathrm{2}\eta+\mathrm{3}\:\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{2}\eta}{\mathrm{3}}\:\Rightarrow\theta_{\mathrm{1}} =\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}\eta}{\mathrm{3}} \\ $$$$ \\ $$$${dt}=\sqrt{\frac{{L}}{\mathrm{3}{g}}}\frac{{d}\theta}{\:\sqrt{\eta−\mathrm{cos}\:\theta}} \\ $$$$\int_{\mathrm{0}} ^{{T}_{\mathrm{1}} } {dt}=\sqrt{\frac{{L}}{\mathrm{3}{g}}}\int_{\theta_{\mathrm{0}} } ^{\theta_{\mathrm{1}} } \frac{{d}\theta}{\:\sqrt{\eta−\mathrm{cos}\:\theta}} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\sqrt{\frac{{L}}{\mathrm{3}{g}}}\int_{\mathrm{cos}^{−\mathrm{1}} \eta} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}\eta}{\mathrm{3}}} \frac{{d}\theta}{\:\sqrt{\eta−\mathrm{cos}\:\theta}} \\ $$$$\omega_{\mathrm{1}} =\sqrt{\frac{\mathrm{3}{g}}{{L}}\left(\eta−\mathrm{cos}\:\theta_{\mathrm{1}} \right)} \\ $$$${u}_{\mathrm{1}} ={u}_{{x}} \mid_{{t}={T}_{\mathrm{1}} } =\frac{{L}\omega_{\mathrm{1}} \:\mathrm{cos}\:\theta_{\mathrm{1}} }{\mathrm{2}}=\frac{\mathrm{cos}\:\theta_{\mathrm{1}} }{\mathrm{2}}\sqrt{\mathrm{3}{gL}\left(\eta−\mathrm{cos}\:\theta_{\mathrm{1}} \right)} \\ $$$${upon}\:{t}={T}_{\mathrm{1}} : \\ $$$${u}_{{x}} ={u}_{\mathrm{1}} =\frac{\mathrm{cos}\:\theta_{\mathrm{1}} }{\mathrm{2}}\sqrt{\mathrm{3}{gL}\left(\eta−\mathrm{cos}\:\theta_{\mathrm{1}} \right)}=\frac{\eta}{\mathrm{3}}\sqrt{\eta{gL}} \\ $$$${v}_{{y}} =\frac{{L}\omega\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mL}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}}+\frac{{m}\left({u}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} \right)}{\mathrm{2}}=\frac{{mg}\left({h}−{y}\right)}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mL}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}}+\frac{{m}}{\mathrm{2}}×\left(\frac{\eta^{\mathrm{3}} {gL}}{\mathrm{9}}+\frac{{L}^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}}\right)=\frac{{mg}\left({h}−{L}\:\mathrm{cos}\:\theta\right)}{\mathrm{2}} \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{12}{g}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}{{L}\left(\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}} \\ $$$$\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{12}{g}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}{{L}\left(\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}} \\ $$$${dt}=\sqrt{\frac{{L}\left(\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}{\mathrm{12}{g}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}}\:{d}\theta \\ $$$$\int_{\mathrm{0}} ^{{T}_{\mathrm{2}} } {dt}=\sqrt{\frac{{L}}{\mathrm{3}{g}}}\int_{\theta_{\mathrm{1}} } ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}}\:{d}\theta \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\sqrt{\frac{{L}}{\mathrm{3}{g}}}\int_{\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}\eta}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}}\:{d}\theta \\ $$$${total}\:{time}\:{needed}: \\ $$$${T}={T}_{\mathrm{1}} +{T}_{\mathrm{2}} =\lambda\sqrt{\frac{{L}}{\mathrm{3}{g}}} \\ $$$${with}\: \\ $$$$\lambda=\int_{\mathrm{cos}^{−\mathrm{1}} \eta} ^{\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}\eta}{\mathrm{3}}} \frac{{d}\theta}{\:\sqrt{\eta−\mathrm{cos}\:\theta}}+\int_{\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}\eta}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}\left(\eta−\frac{\eta^{\mathrm{3}} }{\mathrm{9}}−\mathrm{cos}\:\theta\right)}}\:{d}\theta \\ $$$${example}:\:\eta=\frac{{h}}{{L}}=\mathrm{0}.\mathrm{8} \\ $$$${To}\approx\mathrm{1}.\mathrm{73205081}\sqrt{\frac{{L}}{{g}}} \\ $$
Commented by Tawa11 last updated on 01/Feb/25
$$\mathrm{When}\:\mathrm{will}\:\mathrm{I}\:\mathrm{know}\:\mathrm{book}\:\mathrm{like}\:\mathrm{this}. \\ $$$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
