Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

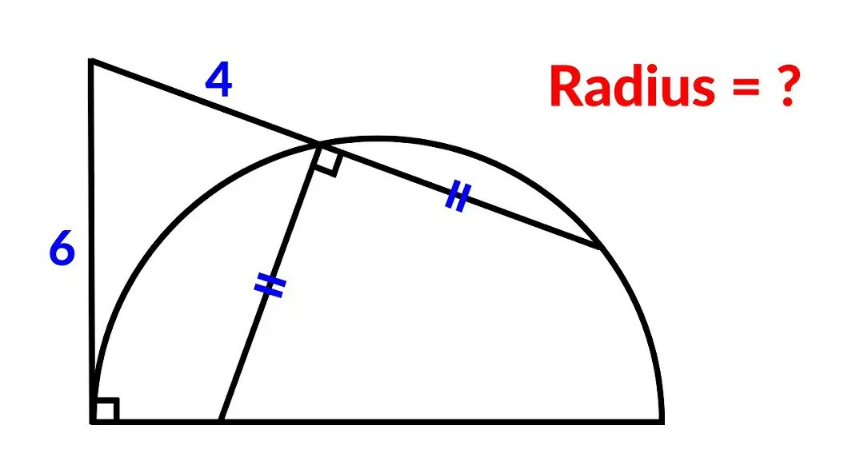
Question Number 216180 by mr W last updated on 29/Jan/25

Answered by AntonCWX last updated on 29/Jan/25

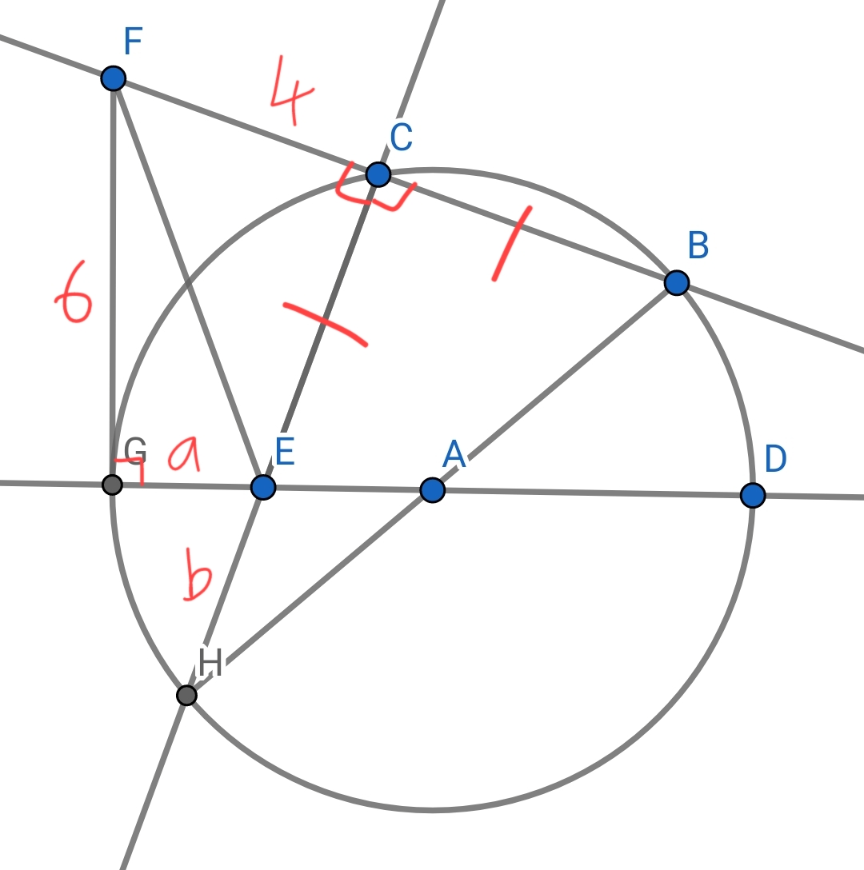
Commented by AntonCWX last updated on 29/Jan/25

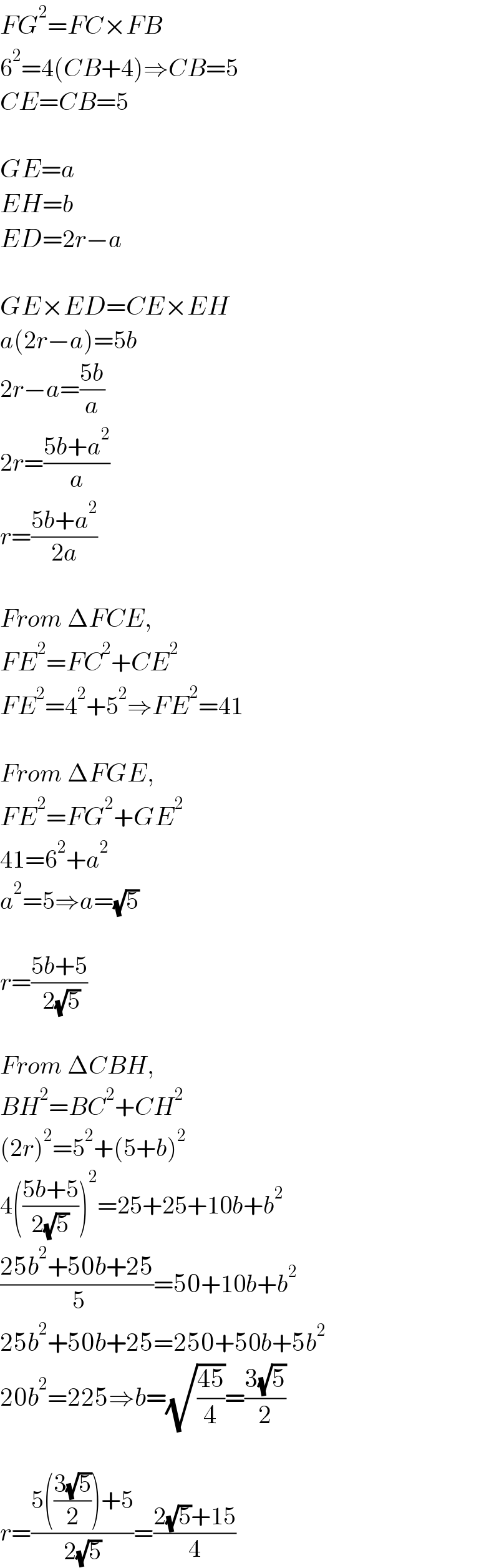
FG^2 =FC×FB 6^2 =4(CB+4)⇒CB=5 CE=CB=5 GE=a EH=b ED=2r−a GE×ED=CE×EH a(2r−a)=5b 2r−a=((5b)/a) 2r=((5b+a^2 )/a) r=((5b+a^2 )/(2a)) From ΔFCE, FE^2 =FC^2 +CE^2 FE^2 =4^2 +5^2 ⇒FE^2 =41 From ΔFGE, FE^2 =FG^2 +GE^2 41=6^2 +a^2 a^2 =5⇒a=(√5) r=((5b+5)/( 2(√5))) From ΔCBH, BH^2 =BC^2 +CH^2 (2r)^2 =5^2 +(5+b)^2 4(((5b+5)/(2(√5))))^2 =25+25+10b+b^2 ((25b^2 +50b+25)/( 5))=50+10b+b^2 25b^2 +50b+25=250+50b+5b^2 20b^2 =225⇒b=(√((45)/4))=((3(√5))/2) r=((5(((3(√5))/2))+5)/(2(√5)))=((2(√5)+15)/4)

$${FG}^{\mathrm{2}} ={FC}×{FB} \\ $$$$\mathrm{6}^{\mathrm{2}} =\mathrm{4}\left({CB}+\mathrm{4}\right)\Rightarrow{CB}=\mathrm{5} \\ $$$${CE}={CB}=\mathrm{5} \\ $$$$ \\ $$$${GE}={a} \\ $$$${EH}={b} \\ $$$${ED}=\mathrm{2}{r}−{a} \\ $$$$ \\ $$$${GE}×{ED}={CE}×{EH} \\ $$$${a}\left(\mathrm{2}{r}−{a}\right)=\mathrm{5}{b} \\ $$$$\mathrm{2}{r}−{a}=\frac{\mathrm{5}{b}}{{a}} \\ $$$$\mathrm{2}{r}=\frac{\mathrm{5}{b}+{a}^{\mathrm{2}} }{{a}} \\ $$$${r}=\frac{\mathrm{5}{b}+{a}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$$ \\ $$$${From}\:\Delta{FCE}, \\ $$$${FE}^{\mathrm{2}} ={FC}^{\mathrm{2}} +{CE}^{\mathrm{2}} \\ $$$${FE}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \Rightarrow{FE}^{\mathrm{2}} =\mathrm{41} \\ $$$$ \\ $$$${From}\:\Delta{FGE}, \\ $$$${FE}^{\mathrm{2}} ={FG}^{\mathrm{2}} +{GE}^{\mathrm{2}} \\ $$$$\mathrm{41}=\mathrm{6}^{\mathrm{2}} +{a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\mathrm{5}\Rightarrow{a}=\sqrt{\mathrm{5}} \\ $$$$ \\ $$$${r}=\frac{\mathrm{5}{b}+\mathrm{5}}{\:\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$ \\ $$$${From}\:\Delta{CBH}, \\ $$$${BH}^{\mathrm{2}} ={BC}^{\mathrm{2}} +{CH}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{r}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\left(\mathrm{5}+{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\frac{\mathrm{5}{b}+\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\mathrm{25}+\mathrm{25}+\mathrm{10}{b}+{b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{25}{b}^{\mathrm{2}} +\mathrm{50}{b}+\mathrm{25}}{\:\mathrm{5}}=\mathrm{50}+\mathrm{10}{b}+{b}^{\mathrm{2}} \\ $$$$\mathrm{25}{b}^{\mathrm{2}} +\mathrm{50}{b}+\mathrm{25}=\mathrm{250}+\mathrm{50}{b}+\mathrm{5}{b}^{\mathrm{2}} \\ $$$$\mathrm{20}{b}^{\mathrm{2}} =\mathrm{225}\Rightarrow{b}=\sqrt{\frac{\mathrm{45}}{\mathrm{4}}}=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$$${r}=\frac{\mathrm{5}\left(\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{15}}{\mathrm{4}} \\ $$

Commented by mr W last updated on 29/Jan/25

��

Answered by A5T last updated on 29/Jan/25

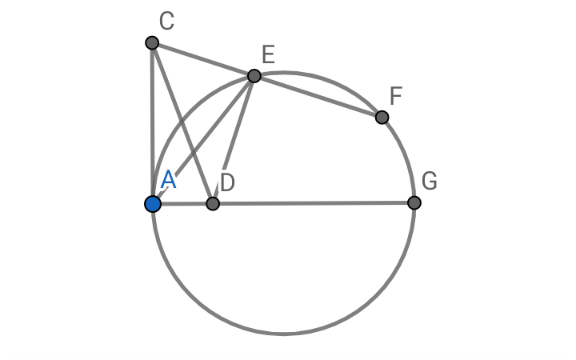
Commented by AntonCWX last updated on 30/Jan/25

I think you mistakenly typed in the 1 there... ((2(√5)+15)/(41)) Remove the 1 and its done.

$${I}\:{think}\:{you}\:{mistakenly}\:{typed}\:{in}\:{the}\:\mathrm{1}\:{there}... \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{15}}{\mathrm{41}} \\ $$$${Remove}\:{the}\:\mathrm{1}\:{and}\:{its}\:{done}. \\ $$

Commented by A5T last updated on 30/Jan/25

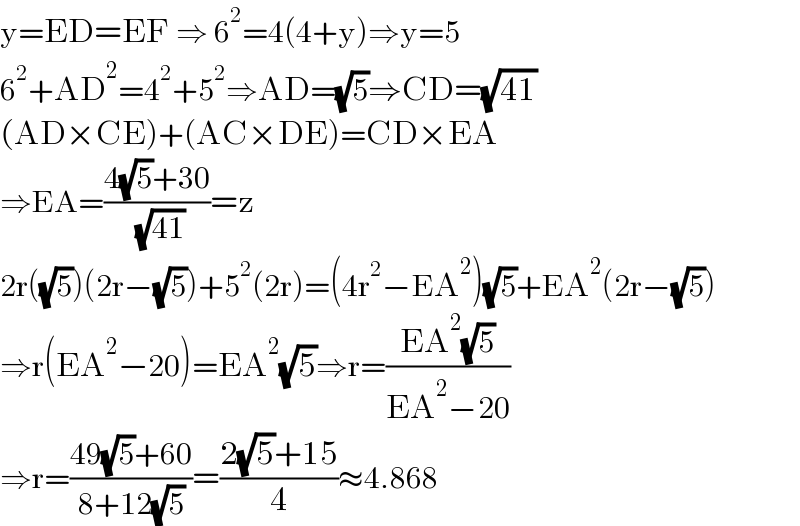
y=ED=EF ⇒ 6^2 =4(4+y)⇒y=5 6^2 +AD^2 =4^2 +5^2 ⇒AD=(√5)⇒CD=(√(41)) (AD×CE)+(AC×DE)=CD×EA ⇒EA=((4(√5)+30)/( (√(41))))=z 2r((√5))(2r−(√5))+5^2 (2r)=(4r^2 −EA^2 )(√5)+EA^2 (2r−(√5)) ⇒r(EA^2 −20)=EA^2 (√5)⇒r=((EA^2 (√5))/(EA^2 −20)) ⇒r=((49(√5)+60)/(8+12(√5)))=((2(√5)+15)/4)≈4.868

$$\mathrm{y}=\mathrm{ED}=\mathrm{EF}\:\Rightarrow\:\mathrm{6}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{4}+\mathrm{y}\right)\Rightarrow\mathrm{y}=\mathrm{5} \\ $$$$\mathrm{6}^{\mathrm{2}} +\mathrm{AD}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \Rightarrow\mathrm{AD}=\sqrt{\mathrm{5}}\Rightarrow\mathrm{CD}=\sqrt{\mathrm{41}} \\ $$$$\left(\mathrm{AD}×\mathrm{CE}\right)+\left(\mathrm{AC}×\mathrm{DE}\right)=\mathrm{CD}×\mathrm{EA}\: \\ $$$$\Rightarrow\mathrm{EA}=\frac{\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{30}}{\:\sqrt{\mathrm{41}}}=\mathrm{z} \\ $$$$\mathrm{2r}\left(\sqrt{\mathrm{5}}\right)\left(\mathrm{2r}−\sqrt{\mathrm{5}}\right)+\mathrm{5}^{\mathrm{2}} \left(\mathrm{2r}\right)=\left(\mathrm{4r}^{\mathrm{2}} −\mathrm{EA}^{\mathrm{2}} \right)\sqrt{\mathrm{5}}+\mathrm{EA}^{\mathrm{2}} \left(\mathrm{2r}−\sqrt{\mathrm{5}}\right) \\ $$$$\Rightarrow\mathrm{r}\left(\mathrm{EA}^{\mathrm{2}} −\mathrm{20}\right)=\mathrm{EA}^{\mathrm{2}} \sqrt{\mathrm{5}}\Rightarrow\mathrm{r}=\frac{\mathrm{EA}^{\mathrm{2}} \sqrt{\mathrm{5}}}{\mathrm{EA}^{\mathrm{2}} −\mathrm{20}} \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{49}\sqrt{\mathrm{5}}+\mathrm{60}}{\mathrm{8}+\mathrm{12}\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{15}}{\mathrm{4}}\approx\mathrm{4}.\mathrm{868} \\ $$

Commented by A5T last updated on 30/Jan/25

It was a typo, thanks.

$$\mathrm{It}\:\mathrm{was}\:\mathrm{a}\:\mathrm{typo},\:\mathrm{thanks}. \\ $$

Commented by mr W last updated on 29/Jan/25

��

Answered by mr W last updated on 29/Jan/25

Commented by mr W last updated on 29/Jan/25

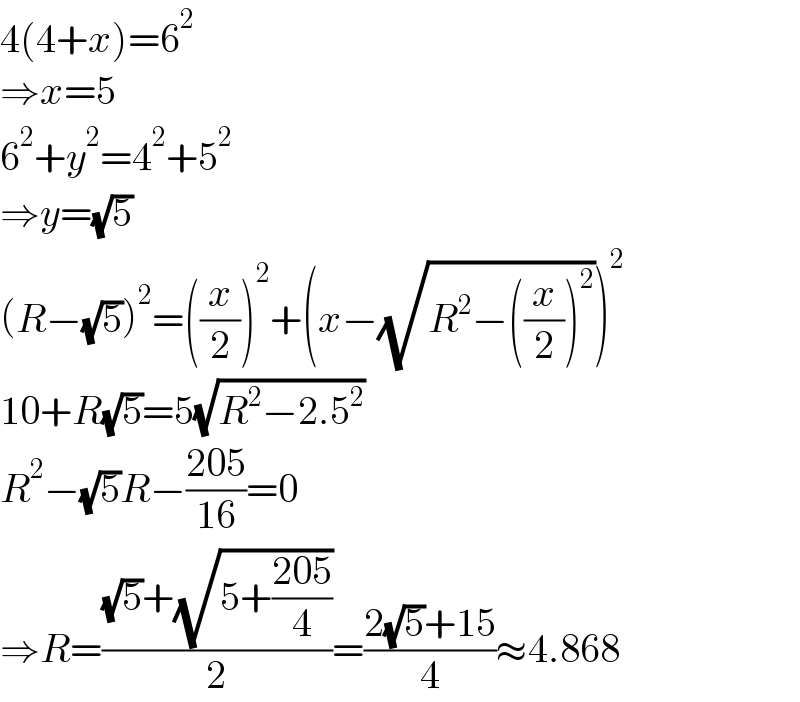
4(4+x)=6^2 ⇒x=5 6^2 +y^2 =4^2 +5^2 ⇒y=(√5) (R−(√5))^2 =((x/2))^2 +(x−(√(R^2 −((x/2))^2 )))^2 10+R(√5)=5(√(R^2 −2.5^2 )) R^2 −(√5)R−((205)/(16))=0 ⇒R=(((√5)+(√(5+((205)/4))))/2)=((2(√5)+15)/4)≈4.868

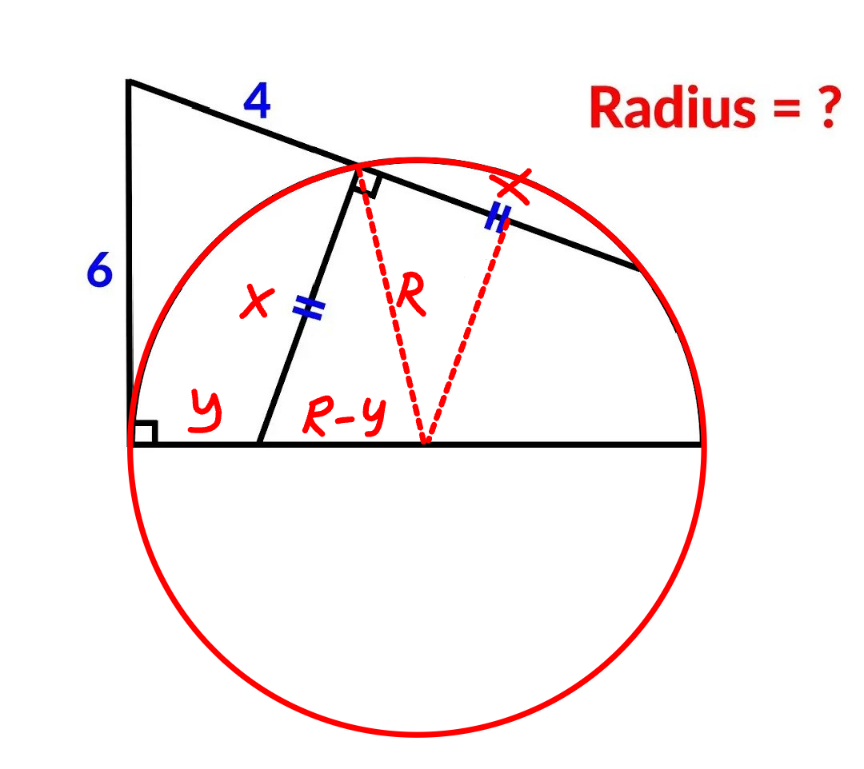
$$\mathrm{4}\left(\mathrm{4}+{x}\right)=\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{5} \\ $$$$\mathrm{6}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{5}} \\ $$$$\left({R}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} =\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({x}−\sqrt{{R}^{\mathrm{2}} −\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\mathrm{10}+{R}\sqrt{\mathrm{5}}=\mathrm{5}\sqrt{{R}^{\mathrm{2}} −\mathrm{2}.\mathrm{5}^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} −\sqrt{\mathrm{5}}{R}−\frac{\mathrm{205}}{\mathrm{16}}=\mathrm{0} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\mathrm{5}}+\sqrt{\mathrm{5}+\frac{\mathrm{205}}{\mathrm{4}}}}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{15}}{\mathrm{4}}\approx\mathrm{4}.\mathrm{868} \\ $$

Answered by A5T last updated on 29/Jan/25

Commented by A5T last updated on 29/Jan/25

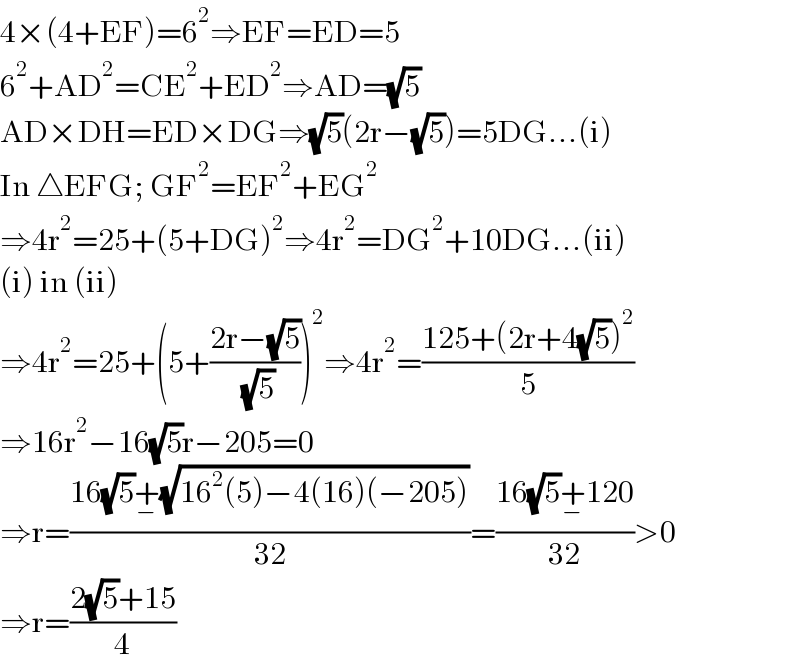
4×(4+EF)=6^2 ⇒EF=ED=5 6^2 +AD^2 =CE^2 +ED^2 ⇒AD=(√5) AD×DH=ED×DG⇒(√5)(2r−(√5))=5DG...(i) In △EFG; GF^2 =EF^2 +EG^2 ⇒4r^2 =25+(5+DG)^2 ⇒4r^2 =DG^2 +10DG...(ii) (i) in (ii) ⇒4r^2 =25+(5+((2r−(√5))/( (√5))))^2 ⇒4r^2 =((125+(2r+4(√5))^2 )/5) ⇒16r^2 −16(√5)r−205=0 ⇒r=((16(√5)+_− (√(16^2 (5)−4(16)(−205))))/(32))=((16(√5)+_− 120)/(32))>0 ⇒r=((2(√5)+15)/4)

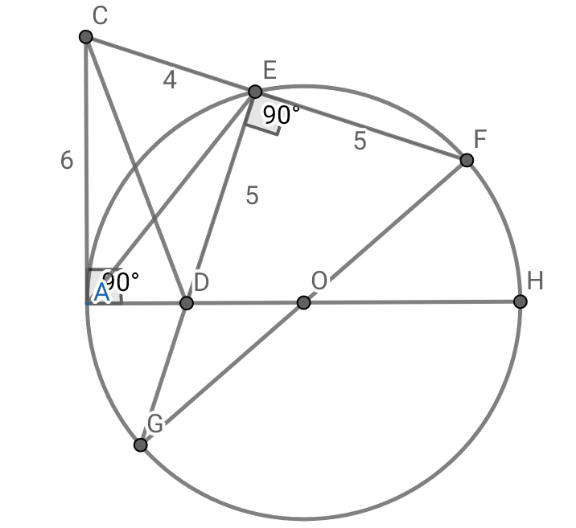
$$\mathrm{4}×\left(\mathrm{4}+\mathrm{EF}\right)=\mathrm{6}^{\mathrm{2}} \Rightarrow\mathrm{EF}=\mathrm{ED}=\mathrm{5} \\ $$$$\mathrm{6}^{\mathrm{2}} +\mathrm{AD}^{\mathrm{2}} =\mathrm{CE}^{\mathrm{2}} +\mathrm{ED}^{\mathrm{2}} \Rightarrow\mathrm{AD}=\sqrt{\mathrm{5}} \\ $$$$\mathrm{AD}×\mathrm{DH}=\mathrm{ED}×\mathrm{DG}\Rightarrow\sqrt{\mathrm{5}}\left(\mathrm{2r}−\sqrt{\mathrm{5}}\right)=\mathrm{5DG}...\left(\mathrm{i}\right) \\ $$$$\mathrm{In}\:\bigtriangleup\mathrm{EFG};\:\mathrm{GF}^{\mathrm{2}} =\mathrm{EF}^{\mathrm{2}} +\mathrm{EG}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4r}^{\mathrm{2}} =\mathrm{25}+\left(\mathrm{5}+\mathrm{DG}\right)^{\mathrm{2}} \Rightarrow\mathrm{4r}^{\mathrm{2}} =\mathrm{DG}^{\mathrm{2}} +\mathrm{10DG}...\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\:\mathrm{in}\:\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{4r}^{\mathrm{2}} =\mathrm{25}+\left(\mathrm{5}+\frac{\mathrm{2r}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \Rightarrow\mathrm{4r}^{\mathrm{2}} =\frac{\mathrm{125}+\left(\mathrm{2r}+\mathrm{4}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{16r}^{\mathrm{2}} −\mathrm{16}\sqrt{\mathrm{5}}\mathrm{r}−\mathrm{205}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{16}\sqrt{\mathrm{5}}\underset{−} {+}\sqrt{\mathrm{16}^{\mathrm{2}} \left(\mathrm{5}\right)−\mathrm{4}\left(\mathrm{16}\right)\left(−\mathrm{205}\right)}}{\mathrm{32}}=\frac{\mathrm{16}\sqrt{\mathrm{5}}\underset{−} {+}\mathrm{120}}{\mathrm{32}}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{15}}{\mathrm{4}} \\ $$

Commented by AntonCWX last updated on 31/Jan/25

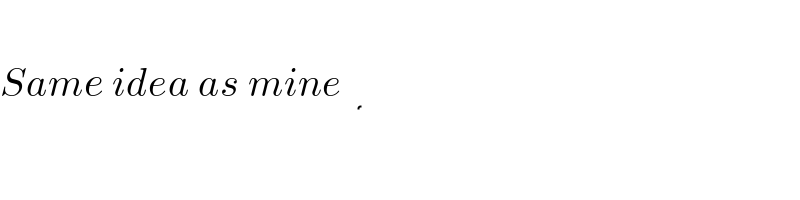
Same idea as mine ⋛

$${Same}\:{idea}\:{as}\:{mine}\:\:\underline{\underbrace{\lesseqgtr}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com