
Question Number 216164 by BaliramKumar last updated on 29/Jan/25

Answered by AntonCWX last updated on 29/Jan/25
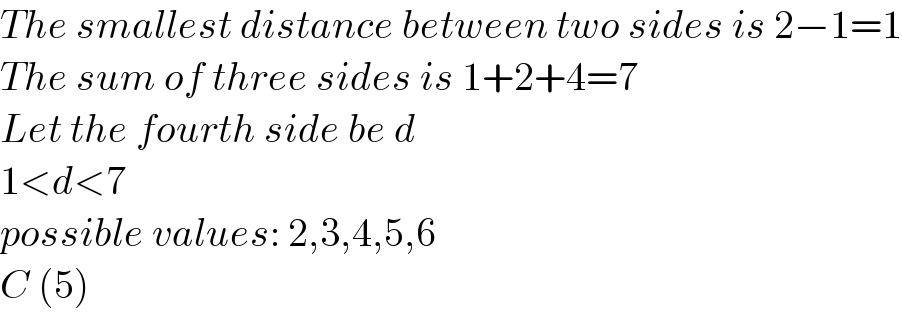
$${The}\:{smallest}\:{distance}\:{between}\:{two}\:{sides}\:{is}\:\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$$${The}\:{sum}\:{of}\:{three}\:{sides}\:{is}\:\mathrm{1}+\mathrm{2}+\mathrm{4}=\mathrm{7} \\ $$$${Let}\:{the}\:{fourth}\:{side}\:{be}\:{d} \\ $$$$\mathrm{1}<{d}<\mathrm{7} \\ $$$${possible}\:{values}:\:\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6} \\ $$$${C}\:\left(\mathrm{5}\right) \\ $$
Answered by Wuji last updated on 29/Jan/25

$$\mathrm{a}=\mathrm{1},\mathrm{b}=\mathrm{2},\mathrm{c}=\mathrm{4} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{4}>\mathrm{d} \\ $$$$\Rightarrow\mathrm{7}>\mathrm{d} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{d}>\mathrm{4}\:\Rightarrow\:\mathrm{d}>\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{4}+\mathrm{d}>\mathrm{2}\:\:\Rightarrow\mathrm{d}>−\mathrm{3} \\ $$$$\mathrm{2}+\mathrm{4}+\mathrm{d}>\mathrm{1}\:\Rightarrow\:\mathrm{d}>−\mathrm{5} \\ $$$$\mathrm{combing}\:\mathrm{the}\:\mathrm{inequalities} \\ $$$$\mathrm{1}<\mathrm{d}<\mathrm{7} \\ $$$$\mathrm{d}\in\mathbb{N} \\ $$$$\mathrm{2},\:\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6} \\ $$$$\mathrm{5}\:\mathrm{possible}\:\mathrm{integer}\:\mathrm{lengths} \\ $$$$\:\mathrm{for}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{side} \\ $$$$ \\ $$
