
Question Number 216162 by Spillover last updated on 28/Jan/25
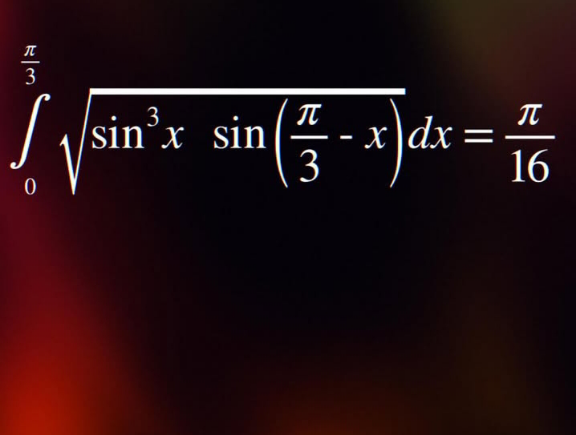
Answered by MrGaster last updated on 02/Feb/25
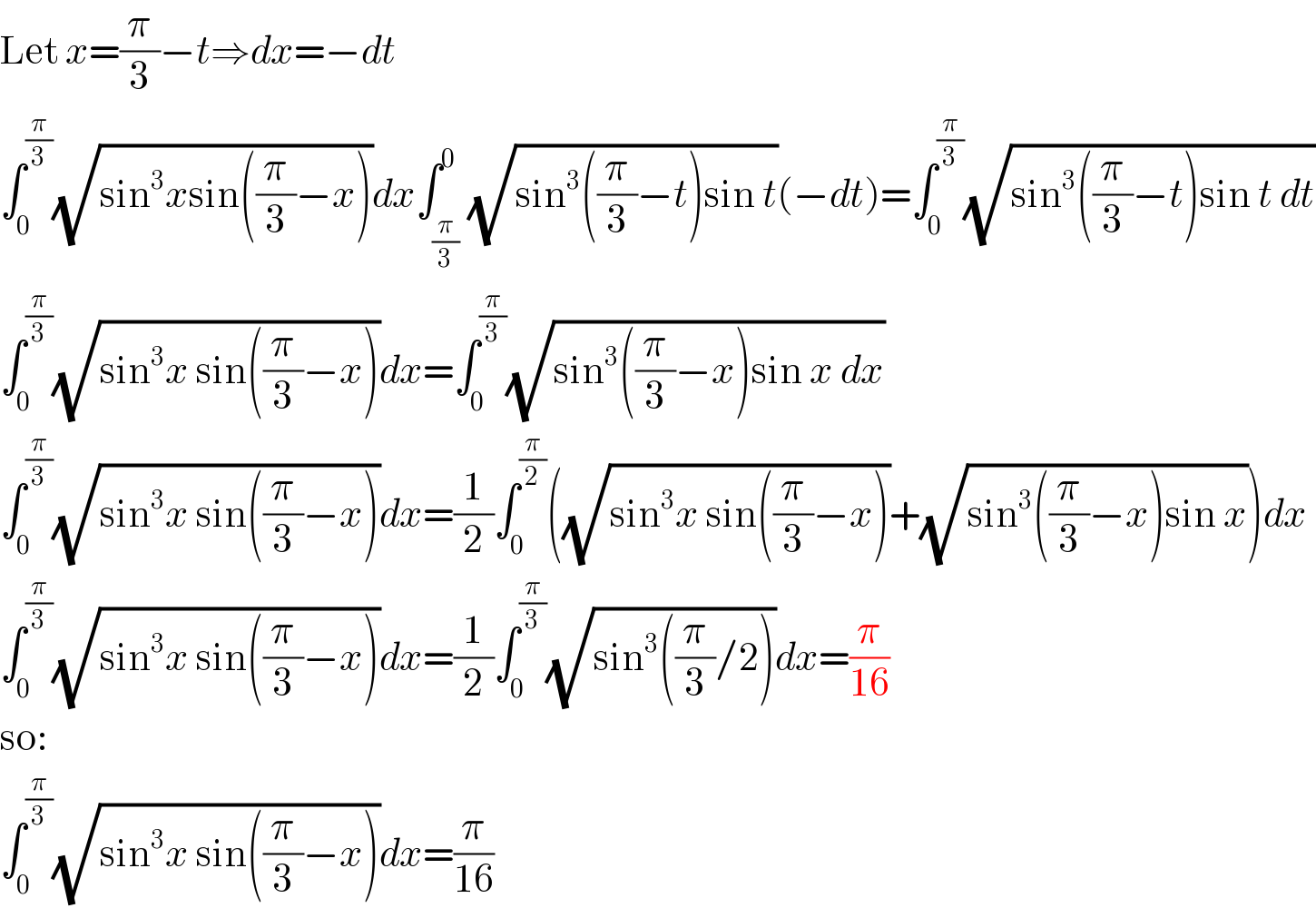
$$\mathrm{Let}\:{x}=\frac{\pi}{\mathrm{3}}−{t}\Rightarrow{dx}=−{dt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} {x}\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{dx}\int_{\frac{\pi}{\mathrm{3}}} ^{\mathrm{0}} \sqrt{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{3}}−{t}\right)\mathrm{sin}\:{t}}\left(−{dt}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{3}}−{t}\right)\mathrm{sin}\:{t}\:{dt}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{3}}−{x}\right)\mathrm{sin}\:{x}\:{dx}} \\ $$$$\int_{\mathrm{0}\:} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}+\sqrt{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{3}}−{x}\right)\mathrm{sin}\:{x}}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{3}}/\mathrm{2}\right)}{dx}=\frac{\pi}{\mathrm{16}} \\ $$$$\mathrm{so}: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{dx}=\frac{\pi}{\mathrm{16}} \\ $$
