
Question Number 216060 by mr W last updated on 26/Jan/25
Commented by mr W last updated on 26/Jan/25
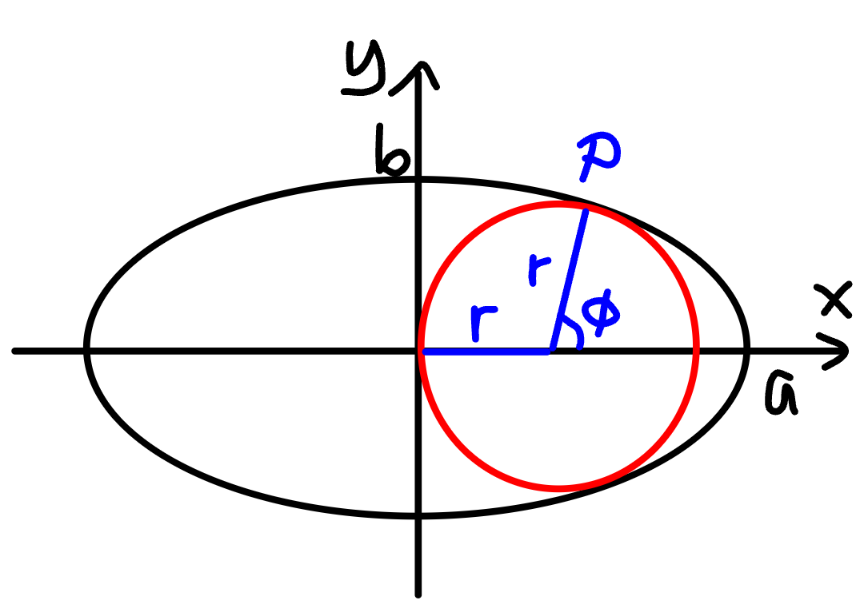
$${find}\:{radius}\:{of}\:{inscribed}\:{circle}\:{r}=? \\ $$
Answered by mr W last updated on 26/Jan/25
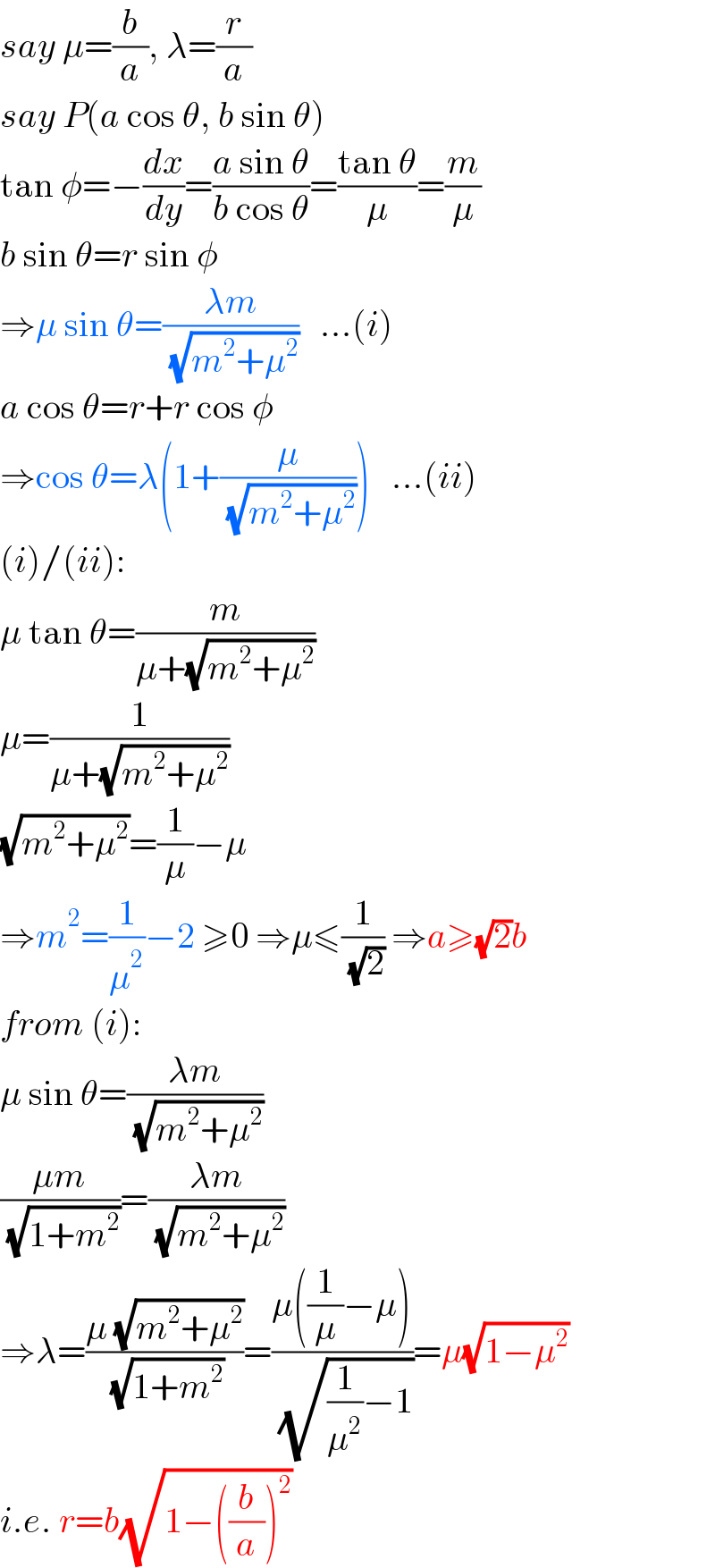
$${say}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{r}}{{a}} \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\phi=−\frac{{dx}}{{dy}}=\frac{{a}\:\mathrm{sin}\:\theta}{{b}\:\mathrm{cos}\:\theta}=\frac{\mathrm{tan}\:\theta}{\mu}=\frac{{m}}{\mu} \\ $$$${b}\:\mathrm{sin}\:\theta={r}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow\mu\:\mathrm{sin}\:\theta=\frac{\lambda{m}}{\:\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }}\:\:\:...\left({i}\right) \\ $$$${a}\:\mathrm{cos}\:\theta={r}+{r}\:\mathrm{cos}\:\phi \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\lambda\left(\mathrm{1}+\frac{\mu}{\:\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }}\right)\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\mu\:\mathrm{tan}\:\theta=\frac{{m}}{\mu+\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }} \\ $$$$\mu=\frac{\mathrm{1}}{\mu+\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }} \\ $$$$\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }=\frac{\mathrm{1}}{\mu}−\mu \\ $$$$\Rightarrow{m}^{\mathrm{2}} =\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\mathrm{2}\:\geqslant\mathrm{0}\:\Rightarrow\mu\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow{a}\geqslant\sqrt{\mathrm{2}}{b} \\ $$$${from}\:\left({i}\right): \\ $$$$\mu\:\mathrm{sin}\:\theta=\frac{\lambda{m}}{\:\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }} \\ $$$$\frac{\mu{m}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{\lambda{m}}{\:\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }} \\ $$$$\Rightarrow\lambda=\frac{\mu\:\sqrt{{m}^{\mathrm{2}} +\mu^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{\mu\left(\frac{\mathrm{1}}{\mu}−\mu\right)}{\:\sqrt{\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\mathrm{1}}}=\mu\sqrt{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$${i}.{e}.\:{r}={b}\sqrt{\mathrm{1}−\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 26/Jan/25
Commented by mr W last updated on 26/Jan/25
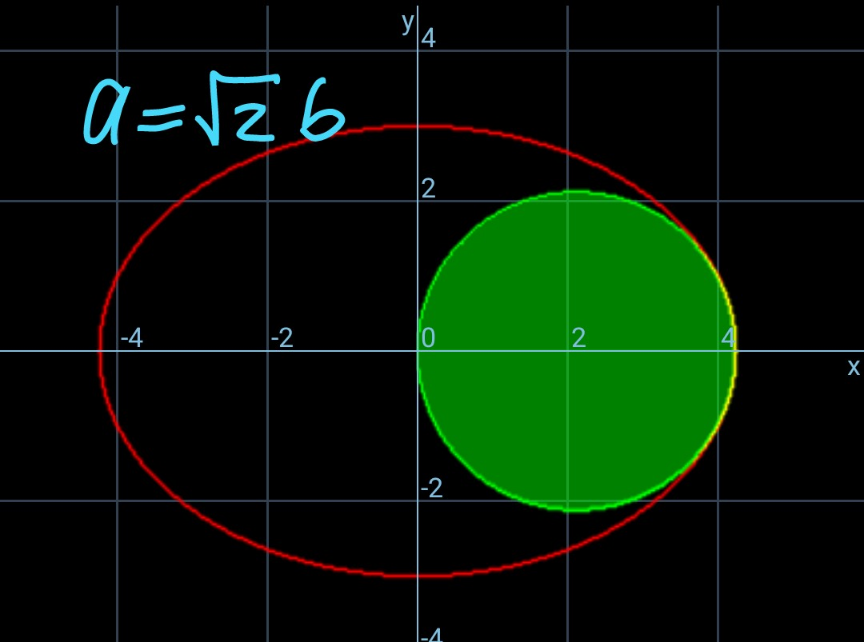
Commented by ajfour last updated on 27/Jan/25
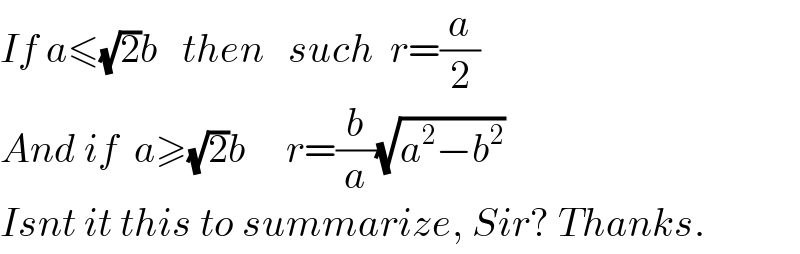
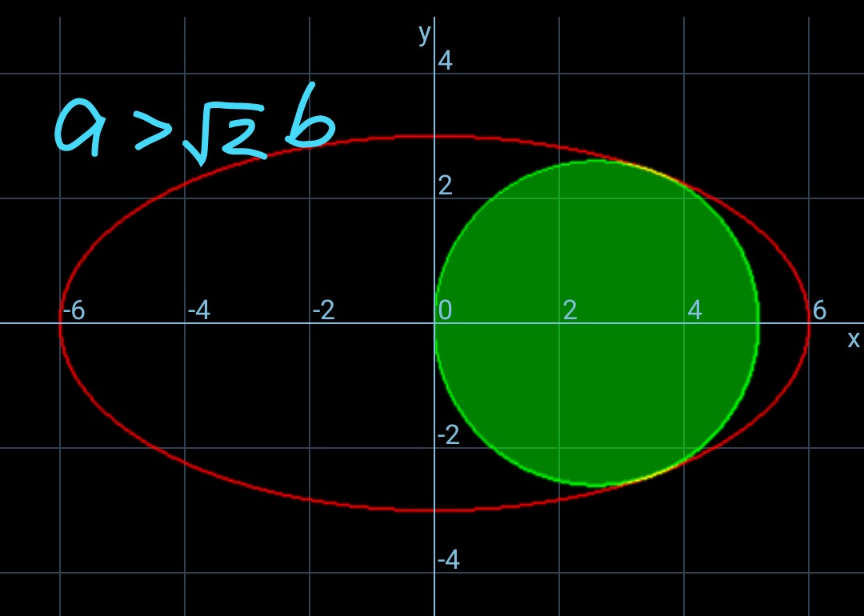
$${If}\:{a}\leqslant\sqrt{\mathrm{2}}{b}\:\:\:{then}\:\:\:{such}\:\:{r}=\frac{{a}}{\mathrm{2}} \\ $$$${And}\:{if}\:\:{a}\geqslant\sqrt{\mathrm{2}}{b}\:\:\:\:\:{r}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${Isnt}\:{it}\:{this}\:{to}\:{summarize},\:{Sir}?\:{Thanks}. \\ $$
Commented by mr W last updated on 27/Jan/25
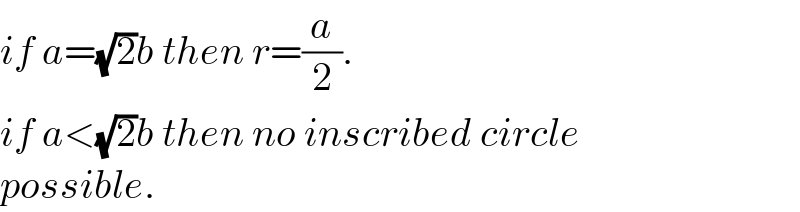
$${if}\:{a}=\sqrt{\mathrm{2}}{b}\:{then}\:{r}=\frac{{a}}{\mathrm{2}}. \\ $$$${if}\:{a}<\sqrt{\mathrm{2}}{b}\:{then}\:{no}\:{inscribed}\:{circle}\: \\ $$$${possible}. \\ $$
Answered by aleks041103 last updated on 27/Jan/25
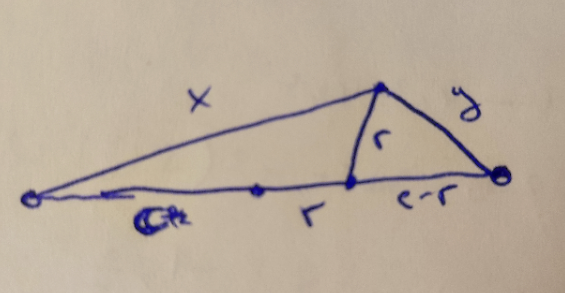
Commented by aleks041103 last updated on 27/Jan/25

$${The}\:{circle}\:{is}\:{tangent}\:{to}\:{the}\:{ellipse}\:{and}\:{therefore} \\ $$$${the}\:{radius}\:{is}\:\bot\:{to}\:{the}\:{tangent}\:{to}\:{the}\:{ellipse} \\ $$$${at}\:{this}\:{point}. \\ $$$${The}\:{tangent}\:{of}\:{an}\:{ellipse}\:{is}\:\bot\:{to}\:{the}\:{angle} \\ $$$${bisector}\:{of}\:{the}\:{angle}\:{between}\:{the}\:{segments} \\ $$$${connecting}\:{point}\:{the}\:{foci}\:{to}\:{the}\:{point}. \\ $$$${Thus}\:{we}\:{get}\:{the}\:{top}\:{schematic}. \\ $$$${Now}: \\ $$$${x}+{y}=\mathrm{2}{a}\:\Rightarrow\:{y}=\mathrm{2}{a}−{x} \\ $$$$\frac{{x}}{{y}}=\frac{{c}+{r}}{{c}−{r}} \\ $$$${xy}−\left({c}+{r}\right)\left({c}−{r}\right)={r}^{\mathrm{2}} \:\Rightarrow\:{xy}={c}^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${c}={a}\sqrt{\mathrm{1}−\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{x}\left(\mathrm{2}{a}−{x}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\Rightarrow\left({x}−{a}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}={a}+{b};{a}−{b} \\ $$$${but}\:{x}>{y}\:\Rightarrow\:{x}={a}+{b},\:{y}={a}−{b} \\ $$$$\Rightarrow\frac{{x}}{{h}}=\frac{{a}+{b}}{{a}−{b}}=\frac{{c}+{r}}{{c}−{r}} \\ $$$$\Rightarrow{r}=\frac{{bc}}{{a}} \\ $$$$\Rightarrow{r}={b}\sqrt{\mathrm{1}−\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} } \\ $$
Commented by aleks041103 last updated on 27/Jan/25

$${The}\:{radius}\:{to}\:{the}\:{point}\:{P}\:\left({original}\:{schematic}\right) \\ $$$${is}\:{perpendicular}\left(\bot\right)\:{to}\:{the}\:{tangent}\:{of}\:{the} \\ $$$${ellipse}\:{at}\:{P}\:\left({since}\:{the}\:{tangent}\:{of}\:{the}\:{circle}\right. \\ $$$$\left.{coinsides}\:{with}\:{the}\:{tangent}\:{to}\:{the}\:{ellipse}\right). \\ $$
Commented by mr W last updated on 27/Jan/25
$${thanks}\:{for}\:{this}\:{nice}\:{solution}! \\ $$
