
Question Number 215820 by Jubr last updated on 18/Jan/25
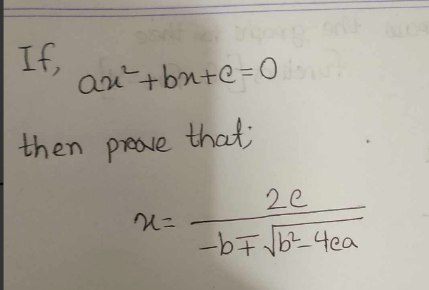
Commented by A5T last updated on 18/Jan/25
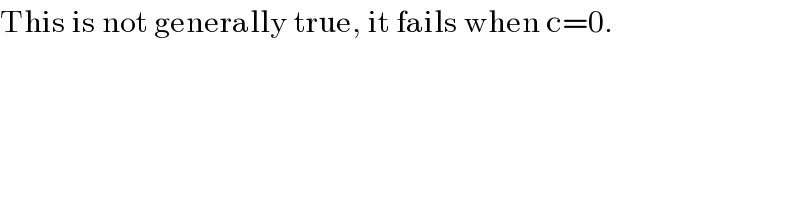
$$\mathrm{This}\:\mathrm{is}\:\mathrm{not}\:\mathrm{generally}\:\mathrm{true},\:\mathrm{it}\:\mathrm{fails}\:\mathrm{when}\:\mathrm{c}=\mathrm{0}. \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jan/25
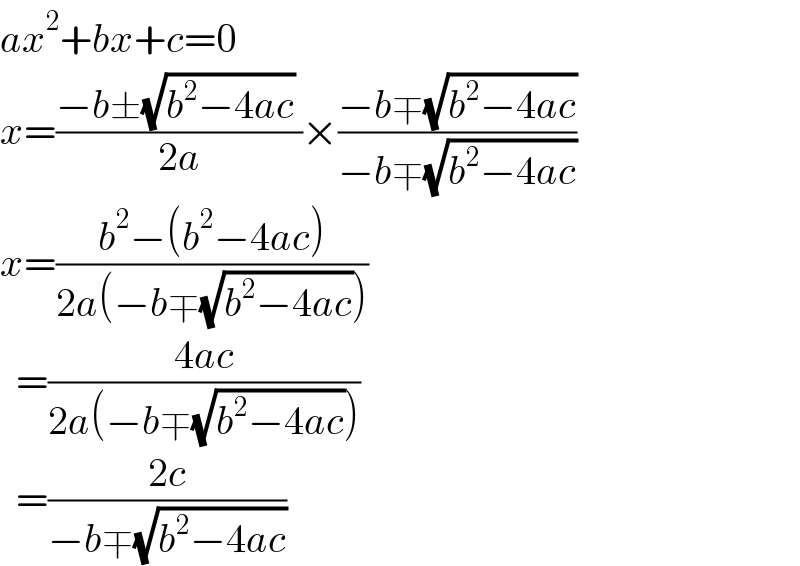
$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\:}{\mathrm{2}{a}}×\frac{−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}} \\ $$$${x}=\frac{{b}^{\mathrm{2}} −\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)}{\mathrm{2}{a}\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)} \\ $$$$\:\:=\frac{\mathrm{4}{ac}}{\mathrm{2}{a}\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)} \\ $$$$\:\:=\frac{\mathrm{2}{c}}{−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}} \\ $$
Commented by Jubr last updated on 19/Jan/25

$${Thanks}\:{sir}. \\ $$
Answered by A5T last updated on 18/Jan/25
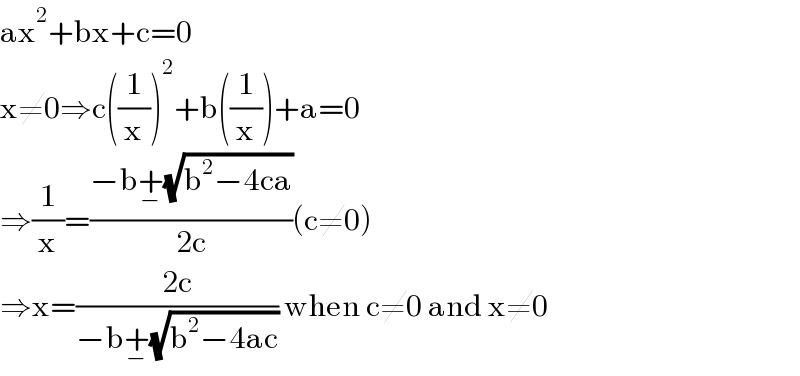
$$\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}=\mathrm{0} \\ $$$$\mathrm{x}\neq\mathrm{0}\Rightarrow\mathrm{c}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{b}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{a}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}=\frac{−\mathrm{b}\underset{−} {+}\sqrt{\mathrm{b}^{\mathrm{2}} −\mathrm{4ca}}}{\mathrm{2c}}\left(\mathrm{c}\neq\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{2c}}{−\mathrm{b}\underset{−} {+}\sqrt{\mathrm{b}^{\mathrm{2}} −\mathrm{4ac}}}\:\mathrm{when}\:\mathrm{c}\neq\mathrm{0}\:\mathrm{and}\:\mathrm{x}\neq\mathrm{0} \\ $$
Commented by Jubr last updated on 19/Jan/25

$${Thanks}\:{sir} \\ $$
