
Question Number 215739 by universe last updated on 16/Jan/25
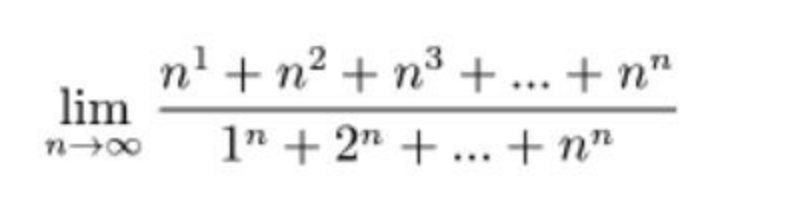
Answered by MrGaster last updated on 19/Jan/25
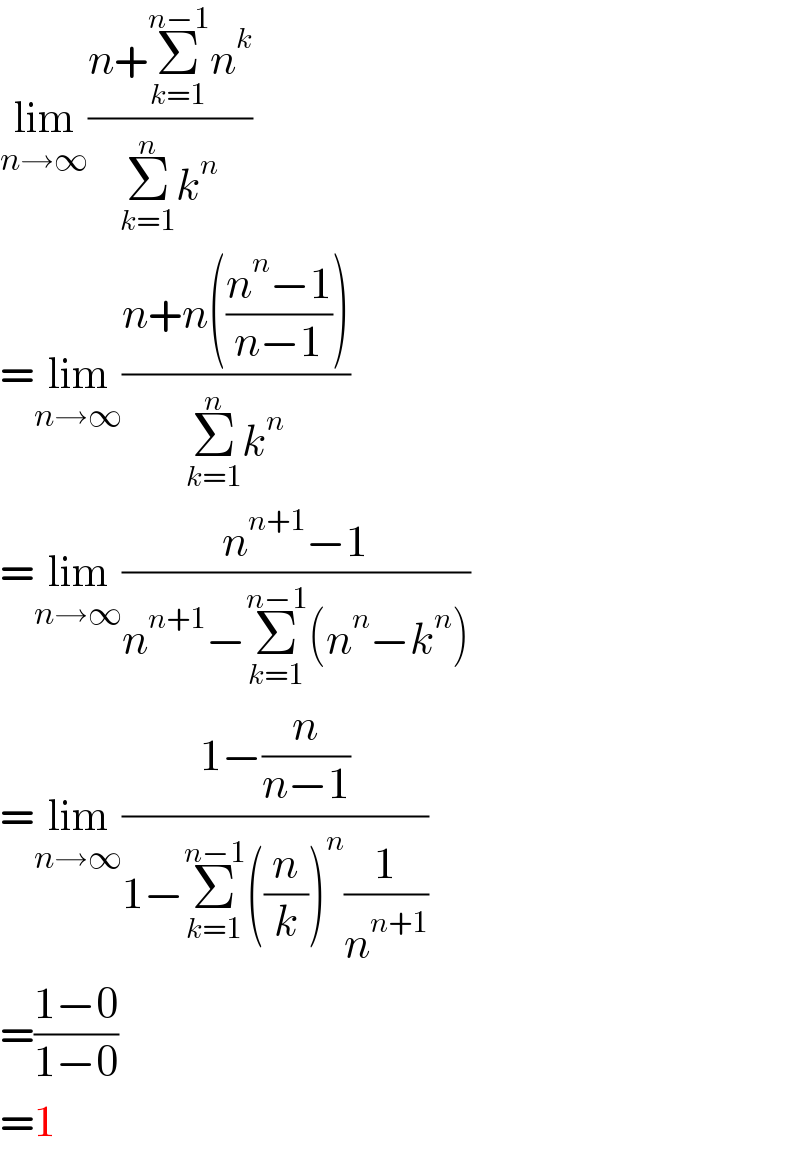
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}+\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{n}^{{k}} }{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{n}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}+{n}\left(\frac{{n}^{{n}} −\mathrm{1}}{{n}−\mathrm{1}}\right)}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{n}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}^{{n}+\mathrm{1}} −\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left({n}^{{n}} −{k}^{{n}} \right)} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\frac{{n}}{{n}−\mathrm{1}}}{\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\frac{{n}}{{k}}\right)^{{n}} \frac{\mathrm{1}}{{n}^{{n}+\mathrm{1}} }} \\ $$$$=\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}−\mathrm{0}} \\ $$$$=\mathrm{1} \\ $$
