Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 215723 by OsamaWafa last updated on 16/Jan/25

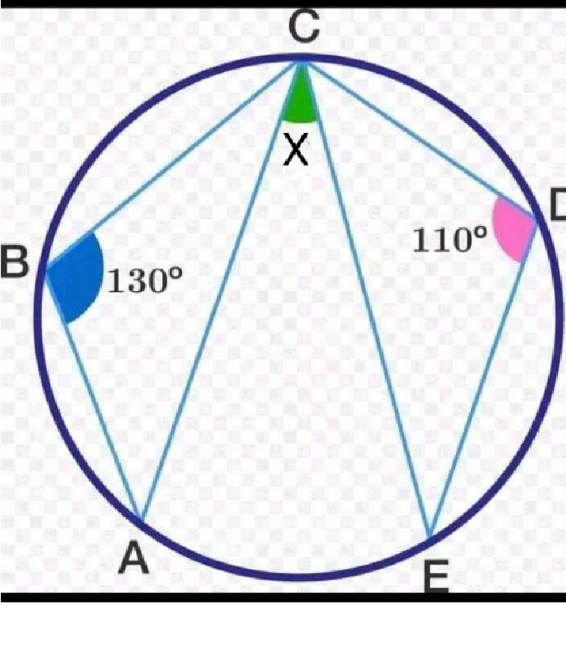
Answered by som(math1967) last updated on 16/Jan/25

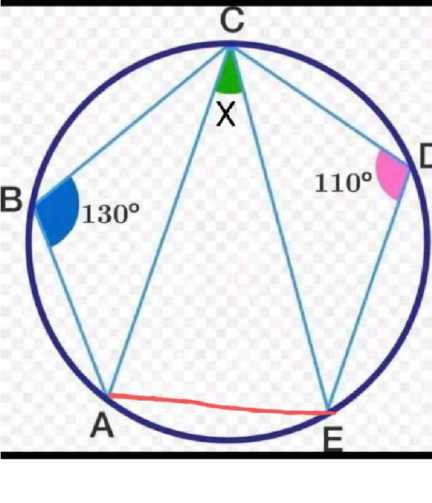
Commented by som(math1967) last updated on 16/Jan/25

∠AEC=180−130=50[ABCE cyclic] ∠CAE=180−110=70[ACDEcyclic] from △ACE x=180−50−70=60

$$\angle{AEC}=\mathrm{180}−\mathrm{130}=\mathrm{50}\left[{ABCE}\:{cyclic}\right] \\ $$$$\angle{CAE}=\mathrm{180}−\mathrm{110}=\mathrm{70}\left[{ACDEcyclic}\right] \\ $$$${from}\:\bigtriangleup{ACE}\: \\ $$$$\:{x}=\mathrm{180}−\mathrm{50}−\mathrm{70}=\mathrm{60} \\ $$

Answered by A5T last updated on 16/Jan/25

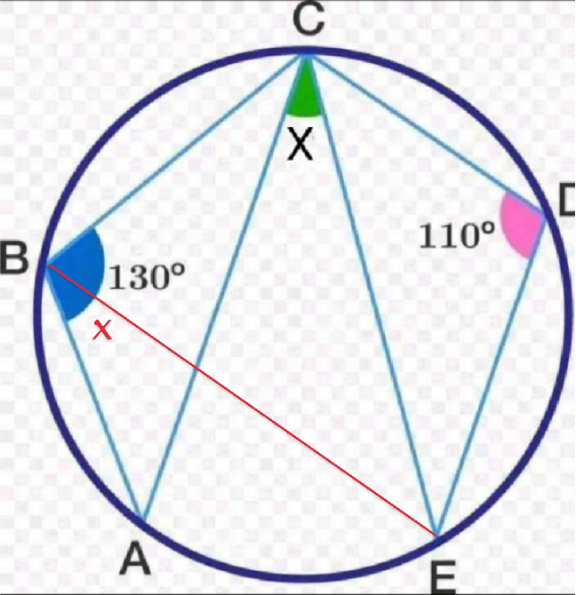
Commented by A5T last updated on 16/Jan/25

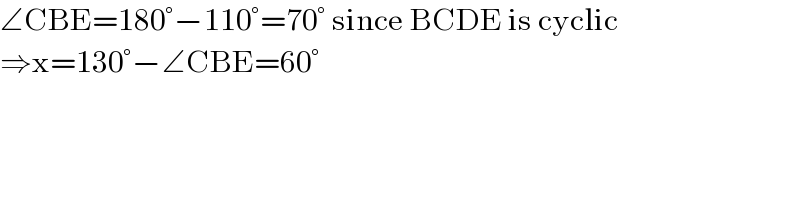
∠CBE=180°−110°=70° since BCDE is cyclic ⇒x=130°−∠CBE=60°

$$\angle\mathrm{CBE}=\mathrm{180}°−\mathrm{110}°=\mathrm{70}°\:\mathrm{since}\:\mathrm{BCDE}\:\mathrm{is}\:\mathrm{cyclic} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{130}°−\angle\mathrm{CBE}=\mathrm{60}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com