Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 215708 by essaad last updated on 15/Jan/25

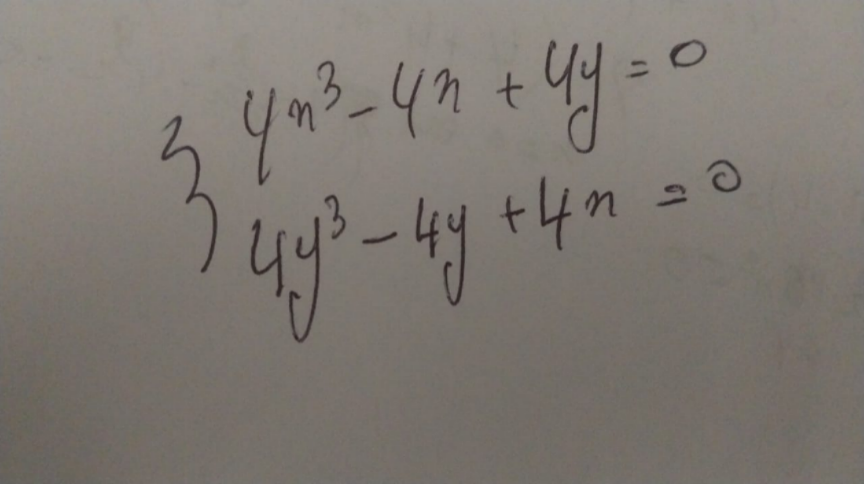
Answered by A5T last updated on 15/Jan/25

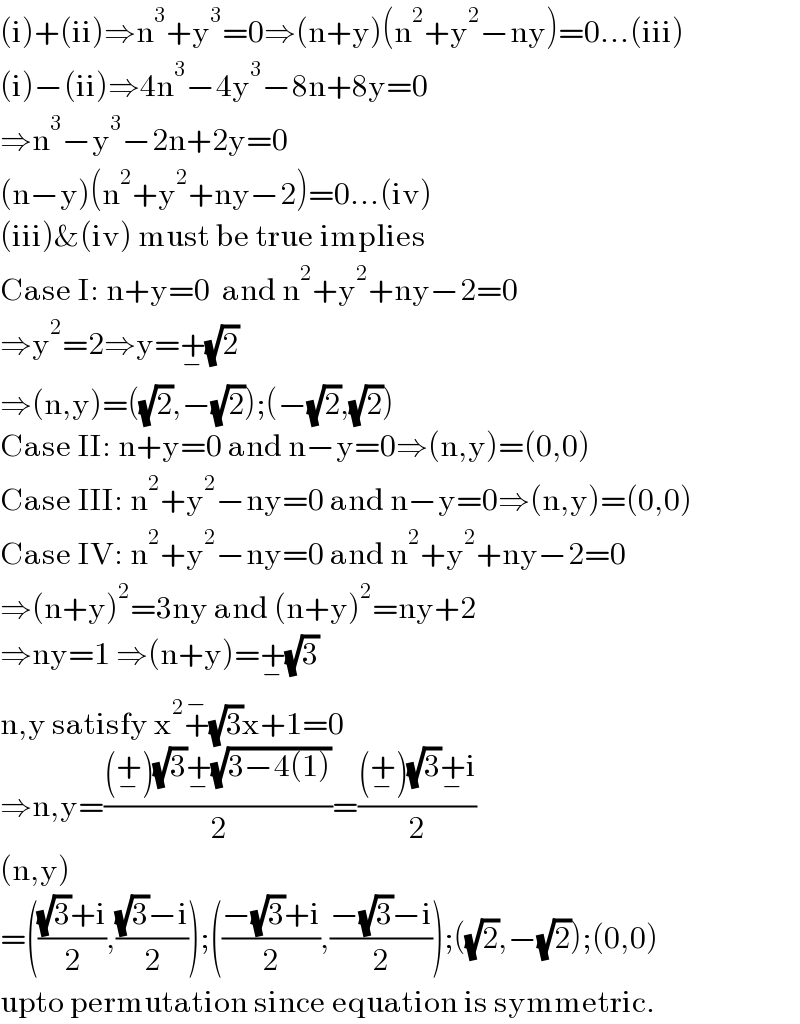
(i)+(ii)⇒n^3 +y^3 =0⇒(n+y)(n^2 +y^2 −ny)=0...(iii) (i)−(ii)⇒4n^3 −4y^3 −8n+8y=0 ⇒n^3 −y^3 −2n+2y=0 (n−y)(n^2 +y^2 +ny−2)=0...(iv) (iii)&(iv) must be true implies Case I: n+y=0 and n^2 +y^2 +ny−2=0 ⇒y^2 =2⇒y=+_− (√2) ⇒(n,y)=((√2),−(√2));(−(√2),(√2)) Case II: n+y=0 and n−y=0⇒(n,y)=(0,0) Case III: n^2 +y^2 −ny=0 and n−y=0⇒(n,y)=(0,0) Case IV: n^2 +y^2 −ny=0 and n^2 +y^2 +ny−2=0 ⇒(n+y)^2 =3ny and (n+y)^2 =ny+2 ⇒ny=1 ⇒(n+y)=+_− (√3) n,y satisfy x^2 +^− (√3)x+1=0 ⇒n,y=(((+_− )(√3)+_− (√(3−4(1))))/2)=(((+_− )(√3)+_− i)/2) (n,y) =((((√3)+i)/2),(((√3)−i)/2));(((−(√3)+i)/2),((−(√3)−i)/2));((√2),−(√2));(0,0) upto permutation since equation is symmetric.

$$\left(\mathrm{i}\right)+\left(\mathrm{ii}\right)\Rightarrow\mathrm{n}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} =\mathrm{0}\Rightarrow\left(\mathrm{n}+\mathrm{y}\right)\left(\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{ny}\right)=\mathrm{0}...\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right)\Rightarrow\mathrm{4n}^{\mathrm{3}} −\mathrm{4y}^{\mathrm{3}} −\mathrm{8n}+\mathrm{8y}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{n}^{\mathrm{3}} −\mathrm{y}^{\mathrm{3}} −\mathrm{2n}+\mathrm{2y}=\mathrm{0} \\ $$$$\left(\mathrm{n}−\mathrm{y}\right)\left(\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{ny}−\mathrm{2}\right)=\mathrm{0}...\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)\&\left(\mathrm{iv}\right)\:\mathrm{must}\:\mathrm{be}\:\mathrm{true}\:\mathrm{implies} \\ $$$$\mathrm{Case}\:\mathrm{I}:\:\mathrm{n}+\mathrm{y}=\mathrm{0}\:\:\mathrm{and}\:\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{ny}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{2}\Rightarrow\mathrm{y}=\underset{−} {+}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{n},\mathrm{y}\right)=\left(\sqrt{\mathrm{2}},−\sqrt{\mathrm{2}}\right);\left(−\sqrt{\mathrm{2}},\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{Case}\:\mathrm{II}:\:\mathrm{n}+\mathrm{y}=\mathrm{0}\:\mathrm{and}\:\mathrm{n}−\mathrm{y}=\mathrm{0}\Rightarrow\left(\mathrm{n},\mathrm{y}\right)=\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{Case}\:\mathrm{III}:\:\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{ny}=\mathrm{0}\:\mathrm{and}\:\mathrm{n}−\mathrm{y}=\mathrm{0}\Rightarrow\left(\mathrm{n},\mathrm{y}\right)=\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{Case}\:\mathrm{IV}:\:\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{ny}=\mathrm{0}\:\mathrm{and}\:\mathrm{n}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{ny}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{n}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{3ny}\:\mathrm{and}\:\left(\mathrm{n}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{ny}+\mathrm{2} \\ $$$$\Rightarrow\mathrm{ny}=\mathrm{1}\:\Rightarrow\left(\mathrm{n}+\mathrm{y}\right)=\underset{−} {+}\sqrt{\mathrm{3}} \\ $$$$\mathrm{n},\mathrm{y}\:\mathrm{satisfy}\:\mathrm{x}^{\mathrm{2}} \overset{−} {+}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{n},\mathrm{y}=\frac{\left(\underset{−} {+}\right)\sqrt{\mathrm{3}}\underset{−} {+}\sqrt{\mathrm{3}−\mathrm{4}\left(\mathrm{1}\right)}}{\mathrm{2}}=\frac{\left(\underset{−} {+}\right)\sqrt{\mathrm{3}}\underset{−} {+}\mathrm{i}}{\mathrm{2}} \\ $$$$\left(\mathrm{n},\mathrm{y}\right) \\ $$$$=\left(\frac{\sqrt{\mathrm{3}}+\mathrm{i}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}−\mathrm{i}}{\mathrm{2}}\right);\left(\frac{−\sqrt{\mathrm{3}}+\mathrm{i}}{\mathrm{2}},\frac{−\sqrt{\mathrm{3}}−\mathrm{i}}{\mathrm{2}}\right);\left(\sqrt{\mathrm{2}},−\sqrt{\mathrm{2}}\right);\left(\mathrm{0},\mathrm{0}\right)\: \\ $$$$\mathrm{upto}\:\mathrm{permutation}\:\mathrm{since}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{symmetric}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com