
Question Number 215704 by universe last updated on 15/Jan/25
Commented by universe last updated on 16/Jan/25
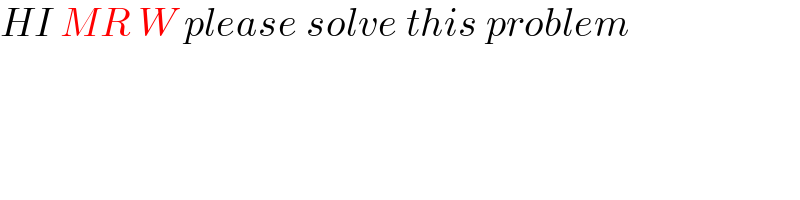
$${HI}\:{MR}\:{W}\:{please}\:{solve}\:{this}\:{problem} \\ $$
Answered by mr W last updated on 16/Jan/25
![∫∫∫(x^2 +y^2 +z^2 )dxdydz =∫_0 ^a ∫_0 ^(a−z) ∫_0 ^(a−z−y) (x^2 +y^2 +z^2 )dxdydz =∫_0 ^a ∫_0 ^(a−z) [(((a−z−y)^3 )/3)+y^2 (a−z−y)+z^2 (a−z−y)]dydz =∫_0 ^a ∫_0 ^(a−z) [(((a−z−y)^3 )/3)+(a−z)y^2 −y^3 +z^2 (a−z)−z^2 y]dydz =∫_0 ^a [(((a−z)^4 )/(3×4))+(((a−z)(a−z)^3 )/3)−(((a−z)^4 )/4)+z^2 (a−z)(a−z)−((z^2 (a−z)^2 )/2)]dz =∫_0 ^a [(((a−z)^4 )/6)+((z^2 (a−z)^2 )/2)]dz =∫_0 ^a [(((a−z)^4 )/6)+((z^4 −2az^3 +a^2 z^2 )/2)]dz =(1/6)×(a^5 /5)+(1/2)((a^5 /5)−((2a×a^4 )/4)+((a^2 ×a^3 )/3)) =(a^5 /(20)) ✓](Q215721.png)
$$\int\int\int\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right){dxdydz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \int_{\mathrm{0}} ^{{a}−{z}} \int_{\mathrm{0}} ^{{a}−{z}−{y}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right){dxdydz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \int_{\mathrm{0}} ^{{a}−{z}} \left[\frac{\left({a}−{z}−{y}\right)^{\mathrm{3}} }{\mathrm{3}}+{y}^{\mathrm{2}} \left({a}−{z}−{y}\right)+{z}^{\mathrm{2}} \left({a}−{z}−{y}\right)\right]{dydz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \int_{\mathrm{0}} ^{{a}−{z}} \left[\frac{\left({a}−{z}−{y}\right)^{\mathrm{3}} }{\mathrm{3}}+\left({a}−{z}\right){y}^{\mathrm{2}} −{y}^{\mathrm{3}} +{z}^{\mathrm{2}} \left({a}−{z}\right)−{z}^{\mathrm{2}} {y}\right]{dydz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \left[\frac{\left({a}−{z}\right)^{\mathrm{4}} }{\mathrm{3}×\mathrm{4}}+\frac{\left({a}−{z}\right)\left({a}−{z}\right)^{\mathrm{3}} }{\mathrm{3}}−\frac{\left({a}−{z}\right)^{\mathrm{4}} }{\mathrm{4}}+{z}^{\mathrm{2}} \left({a}−{z}\right)\left({a}−{z}\right)−\frac{{z}^{\mathrm{2}} \left({a}−{z}\right)^{\mathrm{2}} }{\mathrm{2}}\right]{dz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \left[\frac{\left({a}−{z}\right)^{\mathrm{4}} }{\mathrm{6}}+\frac{{z}^{\mathrm{2}} \left({a}−{z}\right)^{\mathrm{2}} }{\mathrm{2}}\right]{dz} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \left[\frac{\left({a}−{z}\right)^{\mathrm{4}} }{\mathrm{6}}+\frac{{z}^{\mathrm{4}} −\mathrm{2}{az}^{\mathrm{3}} +{a}^{\mathrm{2}} {z}^{\mathrm{2}} }{\mathrm{2}}\right]{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}×\frac{{a}^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{2}{a}×{a}^{\mathrm{4}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} ×{a}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$$=\frac{{a}^{\mathrm{5}} }{\mathrm{20}}\:\checkmark \\ $$
Commented by universe last updated on 16/Jan/25
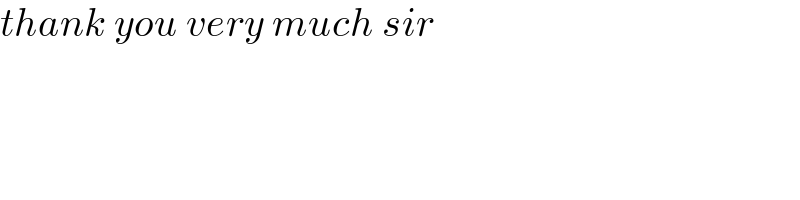
$${thank}\:{you}\:{very}\:{much}\:{sir}\: \\ $$
Commented by universe last updated on 16/Jan/25
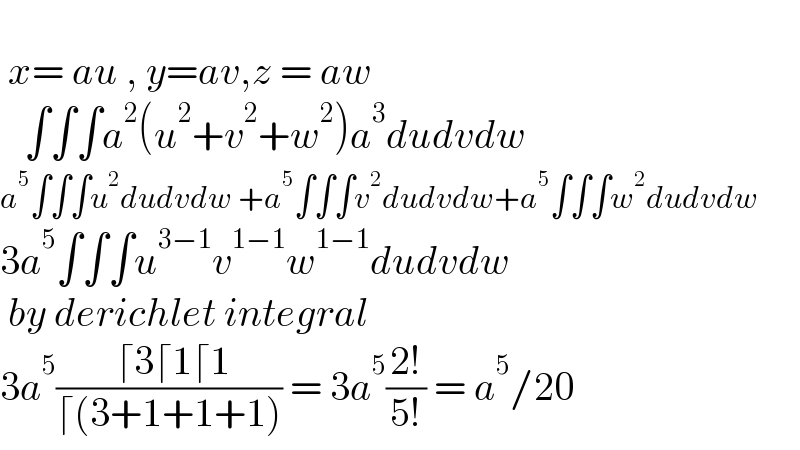
$$ \\ $$$$\:{x}=\:{au}\:,\:{y}={av},{z}\:=\:{aw} \\ $$$$\:\:\:\int\int\int{a}^{\mathrm{2}} \left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} +{w}^{\mathrm{2}} \right){a}^{\mathrm{3}} {dudvdw} \\ $$$${a}^{\mathrm{5}} \int\int\int{u}^{\mathrm{2}} {dudvdw}\:+{a}^{\mathrm{5}} \int\int\int{v}^{\mathrm{2}} {dudvdw}+{a}^{\mathrm{5}} \int\int\int{w}^{\mathrm{2}} {dudvdw} \\ $$$$\mathrm{3}{a}^{\mathrm{5}} \int\int\int{u}^{\mathrm{3}−\mathrm{1}} {v}^{\mathrm{1}−\mathrm{1}} {w}^{\mathrm{1}−\mathrm{1}} {dudvdw} \\ $$$$\:{by}\:{derichlet}\:{integral} \\ $$$$\mathrm{3}{a}^{\mathrm{5}} \frac{\:\lceil\mathrm{3}\lceil\mathrm{1}\lceil\mathrm{1}}{\lceil\left(\mathrm{3}+\mathrm{1}+\mathrm{1}+\mathrm{1}\right)}\:=\:\mathrm{3}{a}^{\mathrm{5}} \frac{\mathrm{2}!}{\mathrm{5}!}\:=\:{a}^{\mathrm{5}} /\mathrm{20} \\ $$
Commented by universe last updated on 16/Jan/25
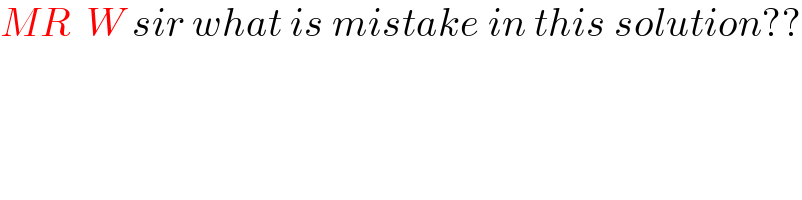
$${MR}\:\:{W}\:{sir}\:{what}\:{is}\:{mistake}\:{in}\:{this}\:{solution}?? \\ $$
Commented by mr W last updated on 16/Jan/25
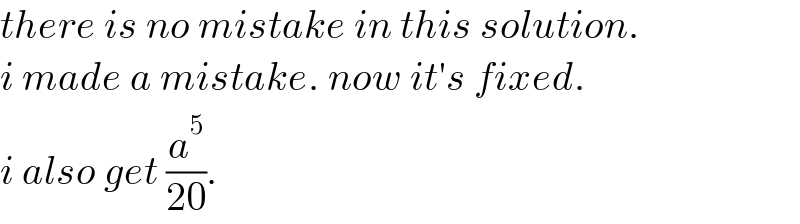
$${there}\:{is}\:{no}\:{mistake}\:{in}\:{this}\:{solution}. \\ $$$${i}\:{made}\:{a}\:{mistake}.\:{now}\:{it}'{s}\:{fixed}. \\ $$$${i}\:{also}\:{get}\:\frac{{a}^{\mathrm{5}} }{\mathrm{20}}. \\ $$
Commented by universe last updated on 16/Jan/25

$${thank}\:{you}\:{sir}\: \\ $$
Commented by ajfour last updated on 17/Jan/25
https://youtu.be/KroW0v7N_Jg?si=8W3jW8TXO6USpeV1
