Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 215679 by BaliramKumar last updated on 14/Jan/25

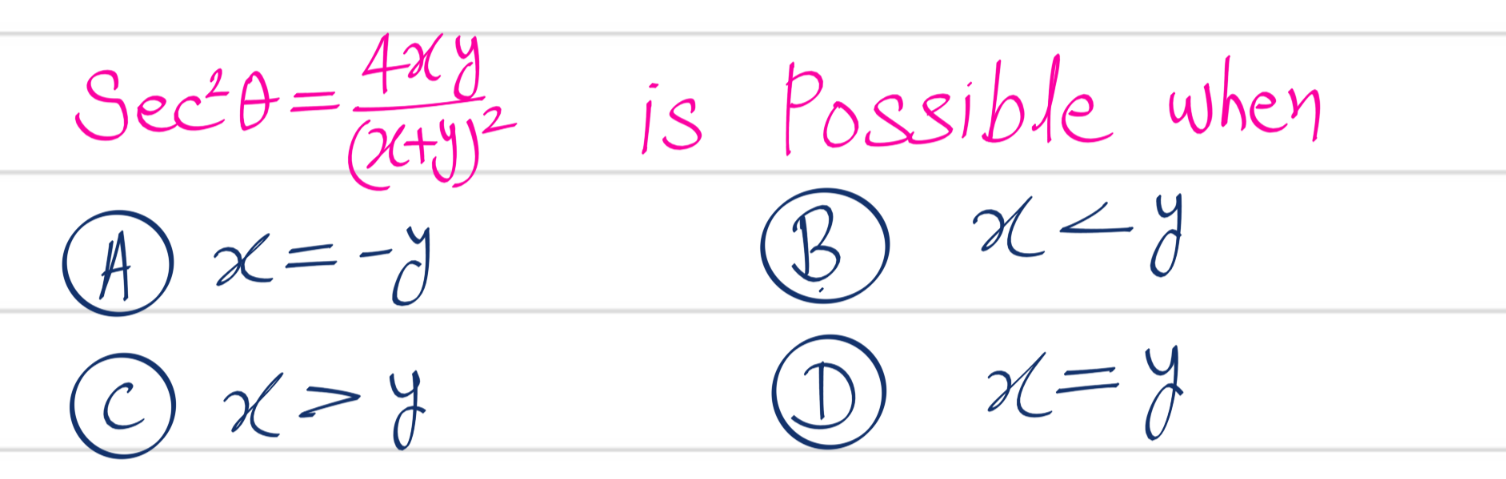
Answered by MATHEMATICSAM last updated on 14/Jan/25

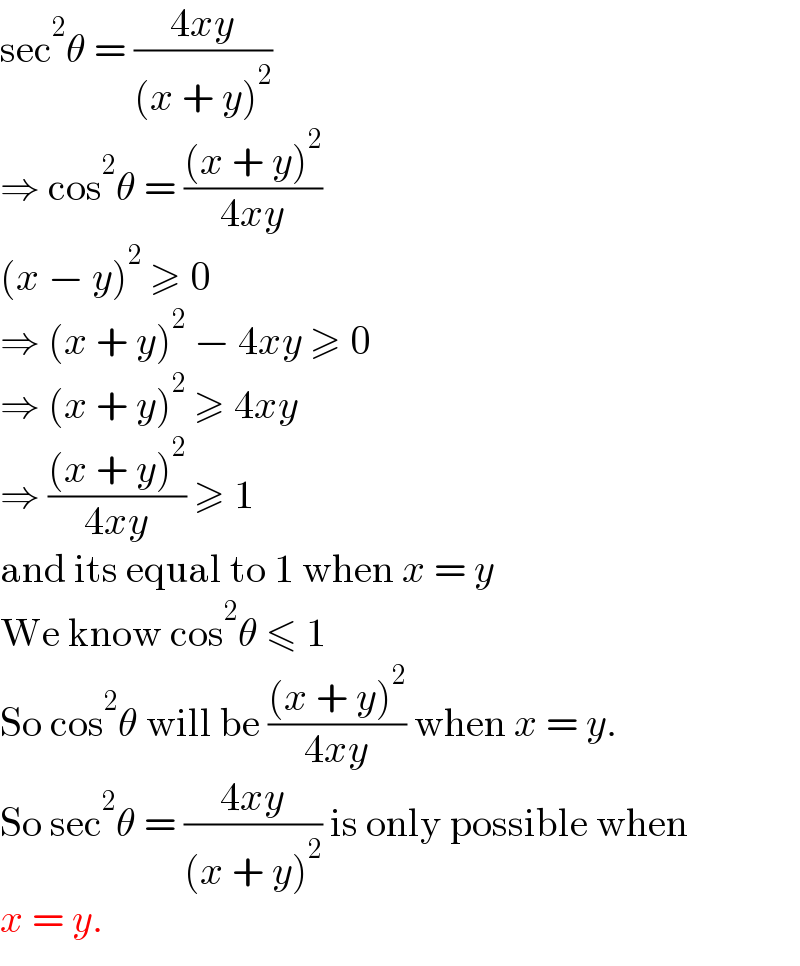
sec^2 θ = ((4xy)/((x + y)^2 )) ⇒ cos^2 θ = (((x + y)^2 )/(4xy)) (x − y)^2 ≥ 0 ⇒ (x + y)^2 − 4xy ≥ 0 ⇒ (x + y)^2 ≥ 4xy ⇒ (((x + y)^2 )/(4xy)) ≥ 1 and its equal to 1 when x = y We know cos^2 θ ≤ 1 So cos^2 θ will be (((x + y)^2 )/(4xy)) when x = y. So sec^2 θ = ((4xy)/((x + y)^2 )) is only possible when x = y.

$$\mathrm{sec}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{4}{xy}}{\left({x}\:+\:{y}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \theta\:=\:\frac{\left({x}\:+\:{y}\right)^{\mathrm{2}} }{\mathrm{4}{xy}} \\ $$$$\left({x}\:−\:{y}\right)^{\mathrm{2}} \:\geqslant\:\mathrm{0}\: \\ $$$$\Rightarrow\:\left({x}\:+\:{y}\right)^{\mathrm{2}} \:−\:\mathrm{4}{xy}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\:\left({x}\:+\:{y}\right)^{\mathrm{2}} \:\geqslant\:\mathrm{4}{xy} \\ $$$$\Rightarrow\:\frac{\left({x}\:+\:{y}\right)^{\mathrm{2}} }{\mathrm{4}{xy}}\:\geqslant\:\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{its}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}\:\mathrm{when}\:{x}\:=\:{y} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{cos}^{\mathrm{2}} \theta\:\leqslant\:\mathrm{1} \\ $$$$\mathrm{So}\:\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{will}\:\mathrm{be}\:\frac{\left({x}\:+\:{y}\right)^{\mathrm{2}} }{\mathrm{4}{xy}}\:\mathrm{when}\:{x}\:=\:{y}. \\ $$$$\mathrm{So}\:\mathrm{sec}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{4}{xy}}{\left({x}\:+\:{y}\right)^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{when} \\ $$$${x}\:=\:{y}. \\ $$

Answered by A5T last updated on 14/Jan/25

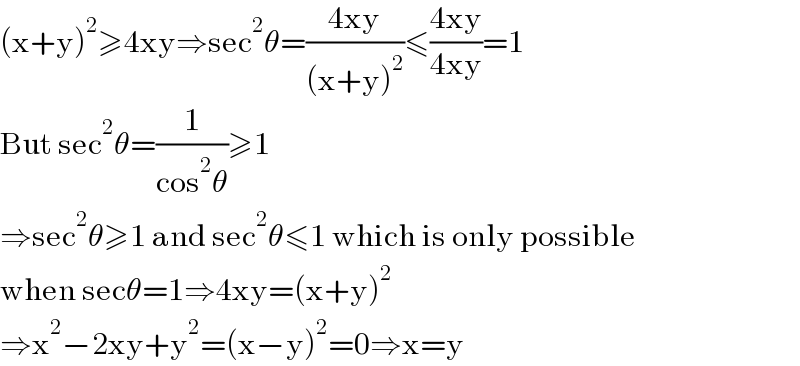
(x+y)^2 ≥4xy⇒sec^2 θ=((4xy)/((x+y)^2 ))≤((4xy)/(4xy))=1 But sec^2 θ=(1/(cos^2 θ))≥1 ⇒sec^2 θ≥1 and sec^2 θ≤1 which is only possible when secθ=1⇒4xy=(x+y)^2 ⇒x^2 −2xy+y^2 =(x−y)^2 =0⇒x=y

$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} \geqslant\mathrm{4xy}\Rightarrow\mathrm{sec}^{\mathrm{2}} \theta=\frac{\mathrm{4xy}}{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} }\leqslant\frac{\mathrm{4xy}}{\mathrm{4xy}}=\mathrm{1} \\ $$$$\mathrm{But}\:\mathrm{sec}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\geqslant\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{sec}^{\mathrm{2}} \theta\geqslant\mathrm{1}\:\mathrm{and}\:\mathrm{sec}^{\mathrm{2}} \theta\leqslant\mathrm{1}\:\mathrm{which}\:\mathrm{is}\:\mathrm{only}\:\mathrm{possible} \\ $$$$\mathrm{when}\:\mathrm{sec}\theta=\mathrm{1}\Rightarrow\mathrm{4xy}=\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{y} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com