Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 215659 by Ari last updated on 13/Jan/25

Answered by Red1ight last updated on 13/Jan/25

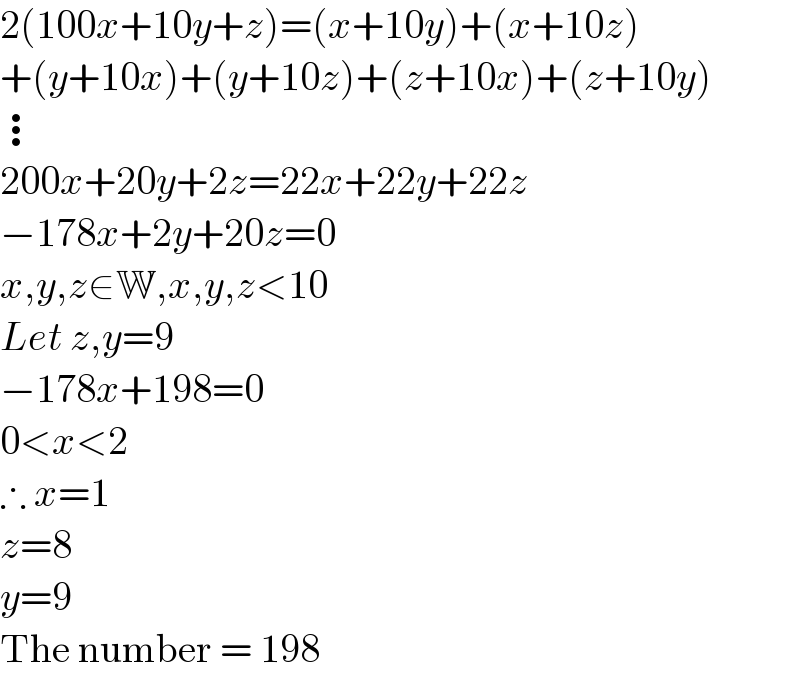
2(100x+10y+z)=(x+10y)+(x+10z) +(y+10x)+(y+10z)+(z+10x)+(z+10y) ⋮ 200x+20y+2z=22x+22y+22z −178x+2y+20z=0 x,y,z∈W,x,y,z<10 Let z,y=9 −178x+198=0 0<x<2 ∴ x=1 z=8 y=9 The number = 198

$$\mathrm{2}\left(\mathrm{100}{x}+\mathrm{10}{y}+{z}\right)=\left({x}+\mathrm{10}{y}\right)+\left({x}+\mathrm{10}{z}\right) \\ $$$$+\left({y}+\mathrm{10}{x}\right)+\left({y}+\mathrm{10}{z}\right)+\left({z}+\mathrm{10}{x}\right)+\left({z}+\mathrm{10}{y}\right) \\ $$$$\vdots \\ $$$$\mathrm{200}{x}+\mathrm{20}{y}+\mathrm{2}{z}=\mathrm{22}{x}+\mathrm{22}{y}+\mathrm{22}{z} \\ $$$$−\mathrm{178}{x}+\mathrm{2}{y}+\mathrm{20}{z}=\mathrm{0} \\ $$$${x},{y},{z}\in\mathbb{W},{x},{y},{z}<\mathrm{10} \\ $$$${Let}\:{z},{y}=\mathrm{9} \\ $$$$−\mathrm{178}{x}+\mathrm{198}=\mathrm{0} \\ $$$$\mathrm{0}<{x}<\mathrm{2} \\ $$$$\therefore\:{x}=\mathrm{1} \\ $$$${z}=\mathrm{8} \\ $$$${y}=\mathrm{9} \\ $$$$\mathrm{The}\:\mathrm{number}\:=\:\mathrm{198} \\ $$

Commented by mr W last updated on 13/Jan/25

right! y=89x−10z 0<89x−10z≤9 10≤10z<89x≤9+10z≤99 ⇒1≤x≤1 ⇒x=1 0<89−10z≤9 10z<89≤9+10z ⇒8≤z≤8 ⇒z=8 ⇒y=89−80=9 the only one number is 198.

$${right}! \\ $$$${y}=\mathrm{89}{x}−\mathrm{10}{z} \\ $$$$\mathrm{0}<\mathrm{89}{x}−\mathrm{10}{z}\leqslant\mathrm{9} \\ $$$$\mathrm{10}\leqslant\mathrm{10}{z}<\mathrm{89}{x}\leqslant\mathrm{9}+\mathrm{10}{z}\leqslant\mathrm{99} \\ $$$$\Rightarrow\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\:\Rightarrow{x}=\mathrm{1} \\ $$$$\mathrm{0}<\mathrm{89}−\mathrm{10}{z}\leqslant\mathrm{9} \\ $$$$\mathrm{10}{z}<\mathrm{89}\leqslant\mathrm{9}+\mathrm{10}{z} \\ $$$$\Rightarrow\mathrm{8}\leqslant{z}\leqslant\mathrm{8}\:\Rightarrow{z}=\mathrm{8} \\ $$$$\Rightarrow{y}=\mathrm{89}−\mathrm{80}=\mathrm{9} \\ $$$${the}\:{only}\:{one}\:{number}\:{is}\:\mathrm{198}. \\ $$

Answered by Rasheed.Sindhi last updated on 14/Jan/25

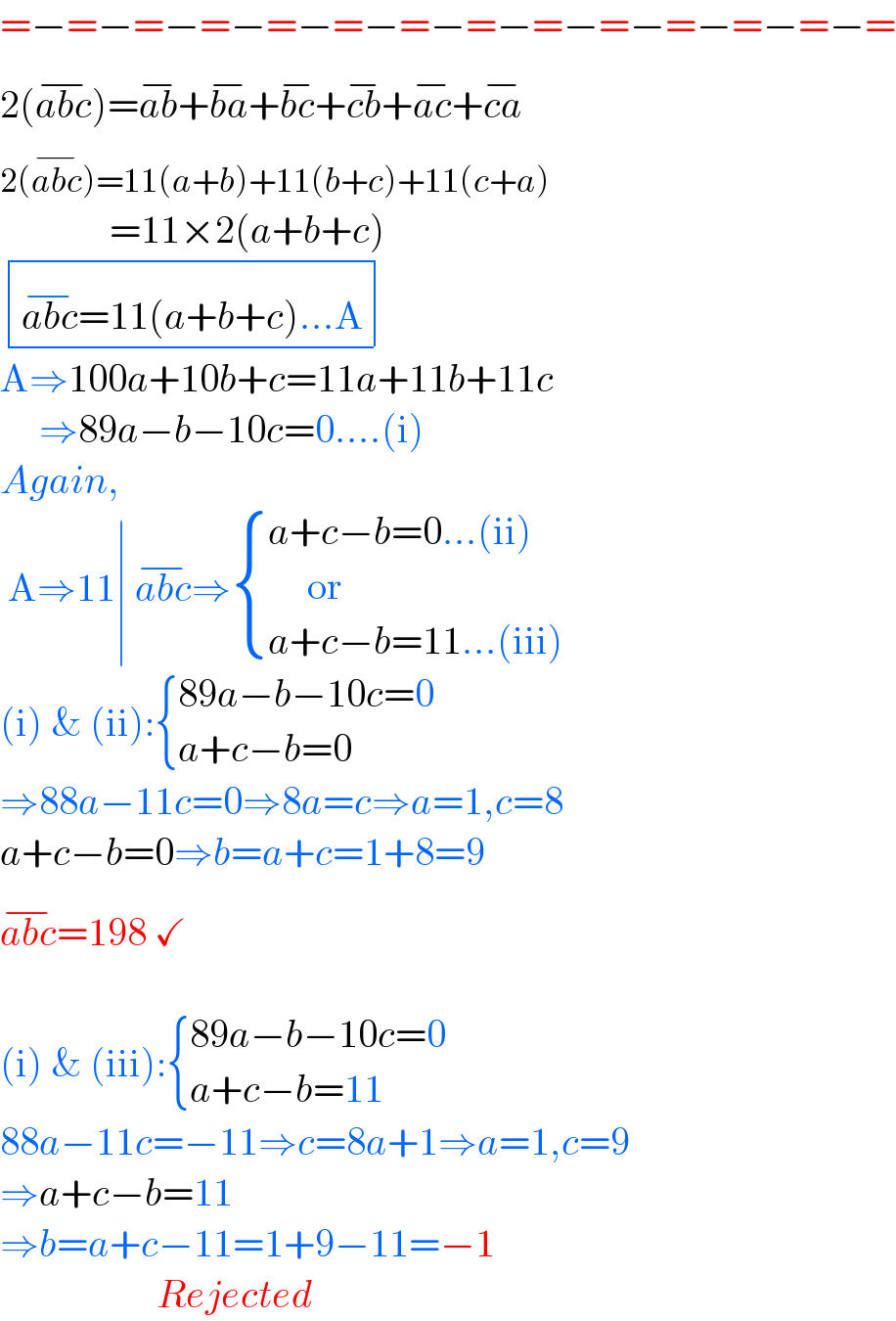
=−=−=−=−=−=−=−=−=−=−=−=−=−= 2(abc^(−) )=ab^(−) +ba^(−) +bc^(−) +cb^(−) +ac^(−) +ca^(−) 2(abc^(−) )=11(a+b)+11(b+c)+11(c+a) =11×2(a+b+c) determinant (((abc^(−) =11(a+b+c)...A))) A⇒100a+10b+c=11a+11b+11c ⇒89a−b−10c=0....(i) Again, A⇒11∣ abc^(−) ⇒ { ((a+c−b=0...(ii) )),(( or)),((a+c−b=11...(iii))) :} (i) & (ii): { ((89a−b−10c=0)),((a+c−b=0)) :} ⇒88a−11c=0⇒8a=c⇒a=1,c=8 a+c−b=0⇒b=a+c=1+8=9 abc^(−) =198 ✓ (i) & (iii): { ((89a−b−10c=0)),((a+c−b=11)) :} 88a−11c=−11⇒c=8a+1⇒a=1,c=9 ⇒a+c−b=11 ⇒b=a+c−11=1+9−11=−1 Rejected

$$=−=−=−=−=−=−=−=−=−=−=−=−=−= \\ $$$$\mathrm{2}\left(\overline {{abc}}\right)=\overline {{ab}}+\overline {{ba}}+\overline {{bc}}+\overline {{cb}}+\overline {{ac}}+\overline {{ca}} \\ $$$$\mathrm{2}\left(\overline {{abc}}\right)=\mathrm{11}\left({a}+{b}\right)+\mathrm{11}\left({b}+{c}\right)+\mathrm{11}\left({c}+{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{11}×\mathrm{2}\left({a}+{b}+{c}\right) \\ $$$$\begin{array}{|c|}{\overline {{abc}}=\mathrm{11}\left({a}+{b}+{c}\right)...\mathrm{A}}\\\hline\end{array} \\ $$$$\mathrm{A}\Rightarrow\mathrm{100}{a}+\mathrm{10}{b}+{c}=\mathrm{11}{a}+\mathrm{11}{b}+\mathrm{11}{c} \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{89}{a}−{b}−\mathrm{10}{c}=\mathrm{0}....\left(\mathrm{i}\right) \\ $$$${Again}, \\ $$$$\:\mathrm{A}\Rightarrow\mathrm{11}\mid\:\overline {{abc}}\Rightarrow\begin{cases}{{a}+{c}−{b}=\mathrm{0}...\left(\mathrm{ii}\right)\:}\\{\:\:\:\:\:\mathrm{or}}\\{{a}+{c}−{b}=\mathrm{11}...\left(\mathrm{iii}\right)}\end{cases} \\ $$$$\left(\mathrm{i}\right)\:\&\:\left(\mathrm{ii}\right):\begin{cases}{\mathrm{89}{a}−{b}−\mathrm{10}{c}=\mathrm{0}}\\{{a}+{c}−{b}=\mathrm{0}}\end{cases}\: \\ $$$$\Rightarrow\mathrm{88}{a}−\mathrm{11}{c}=\mathrm{0}\Rightarrow\mathrm{8}{a}={c}\Rightarrow{a}=\mathrm{1},{c}=\mathrm{8} \\ $$$${a}+{c}−{b}=\mathrm{0}\Rightarrow{b}={a}+{c}=\mathrm{1}+\mathrm{8}=\mathrm{9} \\ $$$$\overline {{abc}}=\mathrm{198}\:\checkmark \\ $$$$\:\: \\ $$$$\left(\mathrm{i}\right)\:\&\:\left(\mathrm{iii}\right):\begin{cases}{\mathrm{89}{a}−{b}−\mathrm{10}{c}=\mathrm{0}}\\{{a}+{c}−{b}=\mathrm{11}}\end{cases}\: \\ $$$$\mathrm{88}{a}−\mathrm{11}{c}=−\mathrm{11}\Rightarrow{c}=\mathrm{8}{a}+\mathrm{1}\Rightarrow{a}=\mathrm{1},{c}=\mathrm{9} \\ $$$$\Rightarrow{a}+{c}−{b}=\mathrm{11} \\ $$$$\Rightarrow{b}={a}+{c}−\mathrm{11}=\mathrm{1}+\mathrm{9}−\mathrm{11}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Rejected} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com