Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 215650 by mr W last updated on 13/Jan/25

Commented by mr W last updated on 14/Jan/25

a rotating disc with angular velocity 𝛚 is put on an incline with rough surface as shown. find the maximum distance the disc can move upwards along the incline. the friction coefficient is 𝛍. (original question see youtube channel from ajfour sir)

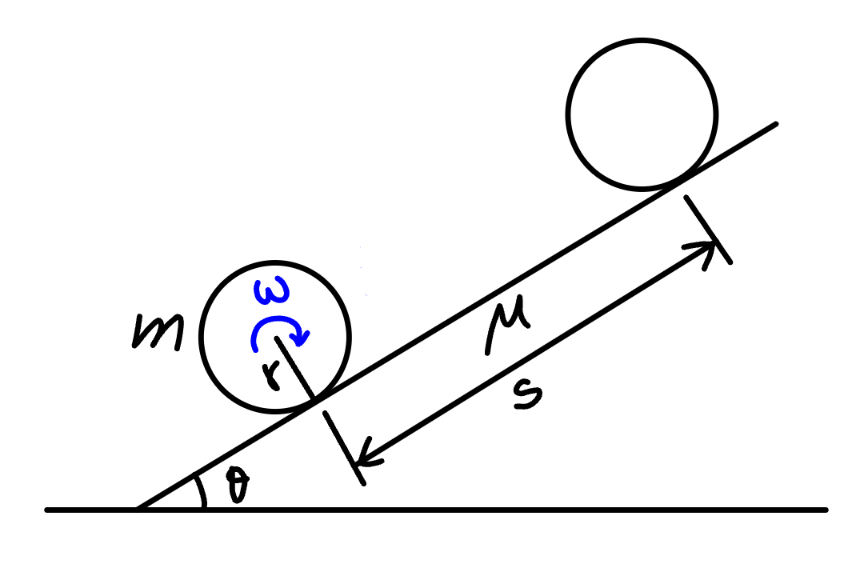
$${a}\:{rotating}\:{disc}\:{with}\:{angular}\:{velocity} \\ $$$$\boldsymbol{\omega}\:{is}\:{put}\:{on}\:{an}\:{incline}\:{with}\:{rough}\: \\ $$$${surface}\:{as}\:{shown}.\: \\ $$$${find}\:{the}\:{maximum}\:{distance}\:{the}\: \\ $$$${disc}\:{can}\:{move}\:{upwards}\:{along}\:{the}\: \\ $$$${incline}. \\ $$$${the}\:{friction}\:{coefficient}\:{is}\:\boldsymbol{\mu}. \\ $$$$ \\ $$$$\left({original}\:{question}\:{see}\:{youtube}\right. \\ $$$$\left.{channel}\:{from}\:{ajfour}\:{sir}\right) \\ $$

Commented by mr W last updated on 15/Jan/25

https://youtu.be/3wiUgK_riz8?si=HlRNIT6W5V9kkg1q

Answered by Wuji last updated on 13/Jan/25

E_(rot) =(1/2)Iω^2 for solid disc, the momment of inertia I is I=(1/2)mr^2 gravutational potential energy at height h E_(grav) =mgh Workdone aginst friction W_f =μmgcosθS from Energy conservation E_(rot) =E_(grav) +W_f (1/4)mr^2 ω^2 =mgh+μmgcosθS S=(((1/4)mr^2 ω^2 −mgh)/(μmgcosθ)) S=((mr^2 ω^2 −4mgh)/(4μmgcosθ)) S=((m(r^2 ω^2 −4gh))/(m(4μgcosθ))) S=((r^2 ω^2 −4gh)/(4μgcosθ))

$$\mathrm{E}_{\mathrm{rot}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}\omega^{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{solid}\:\mathrm{disc},\:\mathrm{the}\:\:\mathrm{momment}\:\mathrm{of} \\ $$$$\mathrm{inertia}\:\mathrm{I}\:\mathrm{is} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{mr}^{\mathrm{2}} \\ $$$$\mathrm{gravutational}\:\mathrm{potential}\:\mathrm{energy} \\ $$$$\mathrm{at}\:\mathrm{height}\:\mathrm{h} \\ $$$$\mathrm{E}_{\mathrm{grav}} =\mathrm{mgh} \\ $$$$\mathrm{Workdone}\:\mathrm{aginst}\:\mathrm{friction} \\ $$$$\mathrm{W}_{\mathrm{f}} =\mu\mathrm{mgcos}\theta\mathrm{S} \\ $$$$\mathrm{from}\:\mathrm{Energy}\:\mathrm{conservation} \\ $$$$\mathrm{E}_{\mathrm{rot}} =\mathrm{E}_{\mathrm{grav}} +\mathrm{W}_{\mathrm{f}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{mr}^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{mgh}+\mu\mathrm{mgcos}\theta\mathrm{S} \\ $$$$\mathrm{S}=\frac{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{mr}^{\mathrm{2}} \omega^{\mathrm{2}} −\mathrm{mgh}}{\mu\mathrm{mgcos}\theta} \\ $$$$\mathrm{S}=\frac{\mathrm{mr}^{\mathrm{2}} \omega^{\mathrm{2}} −\mathrm{4mgh}}{\mathrm{4}\mu\mathrm{mgcos}\theta} \\ $$$$\mathrm{S}=\frac{\mathrm{m}\left(\mathrm{r}^{\mathrm{2}} \omega^{\mathrm{2}} −\mathrm{4gh}\right)}{\mathrm{m}\left(\mathrm{4}\mu\mathrm{gcos}\theta\right)} \\ $$$$\mathrm{S}=\frac{\mathrm{r}^{\mathrm{2}} \omega^{\mathrm{2}} −\mathrm{4gh}}{\mathrm{4}\mu\mathrm{gcos}\theta} \\ $$

Commented by mr W last updated on 13/Jan/25

not correct! only friction by slipping causes loss of energy. but not the whole distance s is slipping. only a part of it is slipping, the other part is rolling. the rolling part doesn′t cause energy loss.

$${not}\:{correct}!\:{only}\:{friction}\:{by}\:{slipping} \\ $$$${causes}\:{loss}\:{of}\:{energy}.\:{but}\:{not}\:{the} \\ $$$${whole}\:{distance}\:{s}\:{is}\:{slipping}.\:{only} \\ $$$${a}\:{part}\:{of}\:{it}\:{is}\:{slipping},\:{the}\:{other} \\ $$$${part}\:{is}\:{rolling}.\:{the}\:{rolling}\:{part} \\ $$$${doesn}'{t}\:{cause}\:{energy}\:{loss}. \\ $$

Answered by mr W last updated on 14/Jan/25

Commented by mr W last updated on 16/Jan/25

case 1: the friction coefficient is large: 𝛍>tan 𝛉 in this case the rotating disc will move upwards along the incline after it is released. for solid disc: I=((mr^2 )/2) t=0 → t_1 : rolling & slipping friction force f=μmg cos θ (↗) a=((μmg cos θ−mg sin θ)/m)=g(μ cos θ−sin θ) α=((fr)/I)=((rμmg cos θ)/((mr^2 )/2))=((2μg cos θ)/r) v_1 =ω_1 r t_1 =(v_1 /a)=((ω−ω_1 )/α) ((ω_1 r)/(g(μ cos θ−sin θ)))=(((ω−ω_1 )r)/(2μg cos θ)) (ω_1 /(μ−tan θ))=((ω−ω_1 )/(2μ)) ⇒ω_1 =(((μ−tan θ)ω)/(3μ−tan θ)) s_1 =(v_1 ^2 /(2a))=(((μ−tan θ)^2 ω^2 r^2 )/(2g(μcos θ−sin θ)(3μ−tan θ)^2 )) ⇒s_1 =(((μ−tan θ)ω^2 r^2 )/(2g(3μ−tan θ)^2 cos θ)) check: rotation of disc ϕ_1 ϕ_1 =((ω^2 −ω_1 ^2 )/(2α))=(r/(4μg cos θ))[1−(((μ−tan θ)^2 )/((3μ−tan θ)^2 ))]ω^2 ϕ_1 r=(((2μ−tan θ)ω^2 r^2 )/(g(3μ−tan θ)^2 cos θ)) > s_1 ⇒ slipping indeed! ϕ_1 =(((2μ−tan θ)ω^2 r)/(g(3μ−tan θ)^2 cos θ)) t=t_1 → t_2 : rolling only K.E. ⇒P.E. (1/2)(((mr^2 )/2)+mr^2 )ω_1 ^2 =mg s_2 sin θ s_2 =((3mr^2 )/(4mg sin θ))×(((μ−tan θ)^2 ω^2 )/((3μ−tan θ)^2 )) ⇒s_2 =((3(μ−tan θ)^2 ω^2 r^2 )/(4g(3μ−tan θ)^2 sin θ)) ϕ_2 =(s_2 /r)=((3(μ−tan θ)^2 ω^2 r)/(4g (3μ−tan θ)^2 sin θ)) ⇒ϕ_2 =((3(μ−tan θ)^2 ω^2 r)/(4g(3μ−tan θ)^2 sin θ)) total distance s=s_1 +s_2 s=(((μ−tan θ)ω^2 r^2 )/(2g(3μ−tan θ)^2 cos θ))+((3(μ−tan θ)^2 ω^2 r^2 )/(4g (3μ−tan θ)^2 sin θ)) ⇒s=(((μ−tan θ)ω^2 r^2 )/(4g(3μ−tan θ) sin θ)) or s sin θ=h=(((μ−tan θ)ω^2 r^2 )/(4g(3μ−tan θ))) mgh′=(1/2)×((mω^2 r^2 )/2) h′=((ω^2 r^2 )/(4g)) we see h=(((μ−tan θ)h′)/(3μ−tan θ))<h′ ϕ=ϕ_1 +ϕ_2 =(((2μ−tan θ)ω^2 r)/(g cos θ (3μ−tan θ)^2 ))+((3(μ−tan θ)^2 ω^2 r)/(4g(3μ−tan θ)^2 sin θ)) ⇒ϕ=(((μ+tan θ)ω^2 r)/(4g(3μ−tan θ) sin θ))

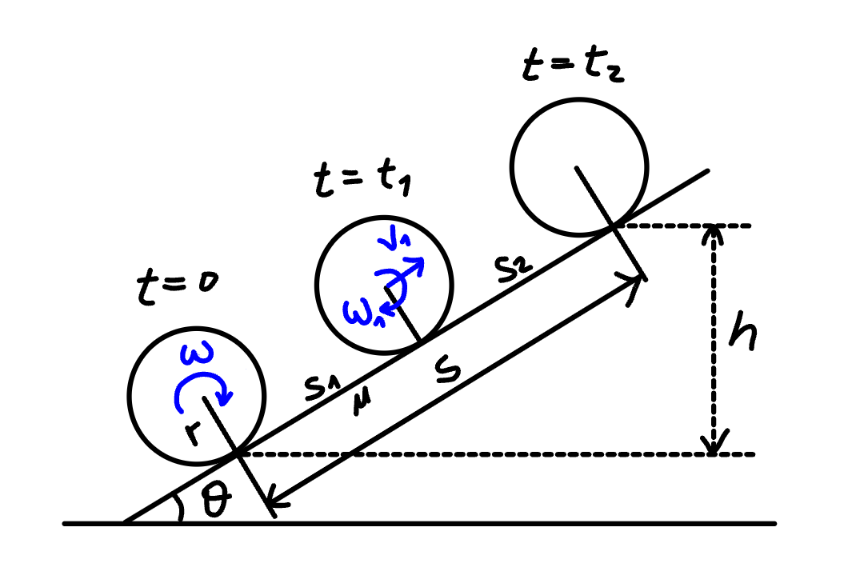
$$\boldsymbol{{case}}\:\mathrm{1}:\:\boldsymbol{{the}}\:\boldsymbol{{friction}}\:\boldsymbol{{coefficient}}\: \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{large}}:\:\boldsymbol{\mu}>\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta} \\ $$$$ \\ $$$${in}\:{this}\:{case}\:{the}\:{rotating}\:{disc}\:{will}\: \\ $$$${move}\:{upwards}\:{along}\:{the}\:{incline}\: \\ $$$${after}\:{it}\:{is}\:{released}. \\ $$$${for}\:{solid}\:{disc}:\:{I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\underline{{t}=\mathrm{0}\:\rightarrow\:{t}_{\mathrm{1}} :\:{rolling}\:\&\:{slipping}} \\ $$$${friction}\:{force}\:{f}=\mu{mg}\:\mathrm{cos}\:\theta\:\:\left(\nearrow\right) \\ $$$${a}=\frac{\mu{mg}\:\mathrm{cos}\:\theta−{mg}\:\mathrm{sin}\:\theta}{{m}}={g}\left(\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$$$\alpha=\frac{{fr}}{{I}}=\frac{{r}\mu{mg}\:\mathrm{cos}\:\theta}{\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{2}\mu{g}\:\mathrm{cos}\:\theta}{{r}} \\ $$$${v}_{\mathrm{1}} =\omega_{\mathrm{1}} {r} \\ $$$${t}_{\mathrm{1}} =\frac{{v}_{\mathrm{1}} }{{a}}=\frac{\omega−\omega_{\mathrm{1}} }{\alpha} \\ $$$$\frac{\omega_{\mathrm{1}} {r}}{{g}\left(\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)}=\frac{\left(\omega−\omega_{\mathrm{1}} \right){r}}{\mathrm{2}\mu{g}\:\mathrm{cos}\:\theta} \\ $$$$\frac{\omega_{\mathrm{1}} }{\mu−\mathrm{tan}\:\theta}=\frac{\omega−\omega_{\mathrm{1}} }{\mathrm{2}\mu} \\ $$$$\Rightarrow\omega_{\mathrm{1}} =\frac{\left(\mu−\mathrm{tan}\:\theta\right)\omega}{\mathrm{3}\mu−\mathrm{tan}\:\theta} \\ $$$${s}_{\mathrm{1}} =\frac{{v}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}{a}}=\frac{\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mu\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{s}_{\mathrm{1}} =\frac{\left(\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \mathrm{cos}\:\theta} \\ $$$${check}: \\ $$$${rotation}\:{of}\:{disc}\:\varphi_{\mathrm{1}} \\ $$$$\varphi_{\mathrm{1}} =\frac{\omega^{\mathrm{2}} −\omega_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\alpha}=\frac{{r}}{\mathrm{4}\mu{g}\:\mathrm{cos}\:\theta}\left[\mathrm{1}−\frac{\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} }{\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} }\right]\omega^{\mathrm{2}} \\ $$$$\varphi_{\mathrm{1}} {r}=\frac{\left(\mathrm{2}\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{cos}\:\theta}\:>\:{s}_{\mathrm{1}} \\ $$$$\Rightarrow\:{slipping}\:{indeed}! \\ $$$$\varphi_{\mathrm{1}} =\frac{\left(\mathrm{2}\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}}{{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{cos}\:\theta} \\ $$$$ \\ $$$$\underline{{t}={t}_{\mathrm{1}} \:\rightarrow\:{t}_{\mathrm{2}} :\:{rolling}\:{only}} \\ $$$${K}.{E}.\:\Rightarrow{P}.{E}. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}+{mr}^{\mathrm{2}} \right)\omega_{\mathrm{1}} ^{\mathrm{2}} ={mg}\:{s}_{\mathrm{2}} \:\mathrm{sin}\:\theta \\ $$$${s}_{\mathrm{2}} =\frac{\mathrm{3}{mr}^{\mathrm{2}} }{\mathrm{4}{mg}\:\mathrm{sin}\:\theta}×\frac{\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{s}_{\mathrm{2}} =\frac{\mathrm{3}\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$$\varphi_{\mathrm{2}} =\frac{{s}_{\mathrm{2}} }{{r}}=\frac{\mathrm{3}\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}}{\mathrm{4}{g}\:\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\varphi_{\mathrm{2}} =\frac{\mathrm{3}\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}}{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$$ \\ $$$${total}\:{distance}\:{s}={s}_{\mathrm{1}} +{s}_{\mathrm{2}} \\ $$$${s}=\frac{\left(\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \mathrm{cos}\:\theta}+\frac{\mathrm{3}\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{g}\:\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{s}=\frac{\left(\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)\:\mathrm{sin}\:\theta} \\ $$$${or} \\ $$$${s}\:\mathrm{sin}\:\theta={h}=\frac{\left(\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)} \\ $$$$ \\ $$$${mgh}'=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{m}\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${h}'=\frac{\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{g}} \\ $$$${we}\:{see}\:{h}=\frac{\left(\mu−\mathrm{tan}\:\theta\right){h}'}{\mathrm{3}\mu−\mathrm{tan}\:\theta}<{h}' \\ $$$$ \\ $$$$\varphi=\varphi_{\mathrm{1}} +\varphi_{\mathrm{2}} =\frac{\left(\mathrm{2}\mu−\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}}{{g}\:\mathrm{cos}\:\theta\:\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} }+\frac{\mathrm{3}\left(\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}}{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\varphi=\frac{\left(\mu+\mathrm{tan}\:\theta\right)\omega^{\mathrm{2}} {r}}{\mathrm{4}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)\:\mathrm{sin}\:\theta} \\ $$

Commented by mr W last updated on 14/Jan/25

Commented by mr W last updated on 14/Jan/25

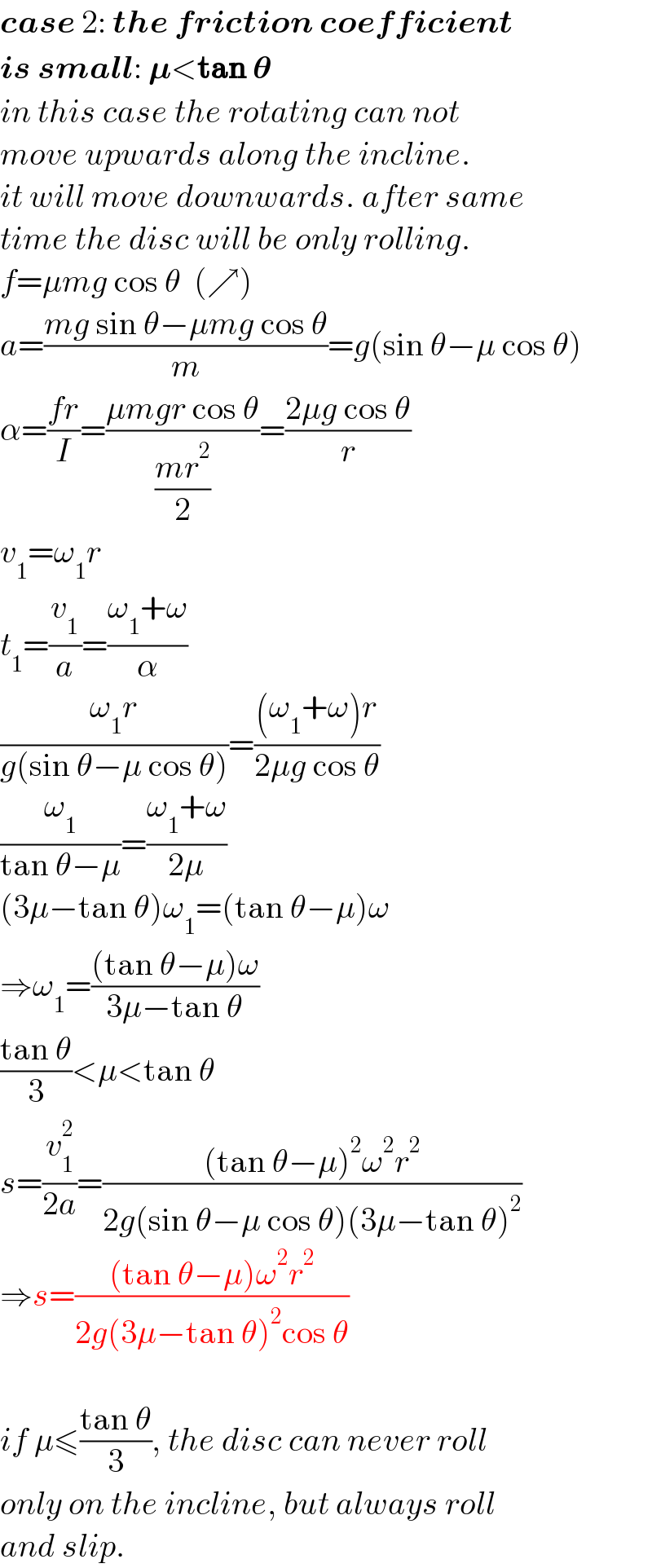
case 2: the friction coefficient is small: 𝛍<tan 𝛉 in this case the rotating can not move upwards along the incline. it will move downwards. after same time the disc will be only rolling. f=μmg cos θ (↗) a=((mg sin θ−μmg cos θ)/m)=g(sin θ−μ cos θ) α=((fr)/I)=((μmgr cos θ)/((mr^2 )/2))=((2μg cos θ)/r) v_1 =ω_1 r t_1 =(v_1 /a)=((ω_1 +ω)/α) ((ω_1 r)/(g(sin θ−μ cos θ)))=(((ω_1 +ω)r)/(2μg cos θ)) (ω_1 /(tan θ−μ))=((ω_1 +ω)/(2μ)) (3μ−tan θ)ω_1 =(tan θ−μ)ω ⇒ω_1 =(((tan θ−μ)ω)/(3μ−tan θ)) ((tan θ)/3)<μ<tan θ s=(v_1 ^2 /(2a))=(((tan θ−μ)^2 ω^2 r^2 )/(2g(sin θ−μ cos θ)(3μ−tan θ)^2 )) ⇒s=(((tan θ−μ)ω^2 r^2 )/(2g(3μ−tan θ)^2 cos θ)) if μ≤((tan θ)/3), the disc can never roll only on the incline, but always roll and slip.

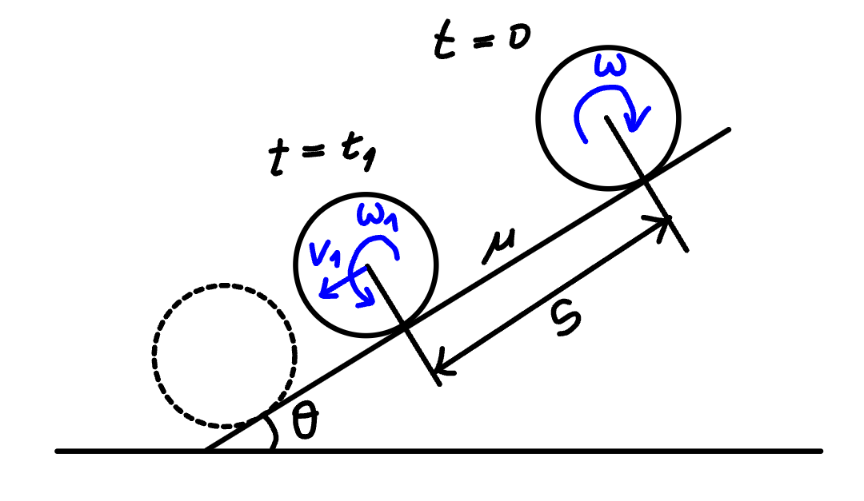
$$\boldsymbol{{case}}\:\mathrm{2}:\:\boldsymbol{{the}}\:\boldsymbol{{friction}}\:\boldsymbol{{coefficient}} \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{small}}:\:\boldsymbol{\mu}<\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta} \\ $$$${in}\:{this}\:{case}\:{the}\:{rotating}\:{can}\:{not} \\ $$$${move}\:{upwards}\:{along}\:{the}\:{incline}. \\ $$$${it}\:{will}\:{move}\:{downwards}.\:{after}\:{same} \\ $$$${time}\:{the}\:{disc}\:{will}\:{be}\:{only}\:{rolling}. \\ $$$${f}=\mu{mg}\:\mathrm{cos}\:\theta\:\:\left(\nearrow\right) \\ $$$${a}=\frac{{mg}\:\mathrm{sin}\:\theta−\mu{mg}\:\mathrm{cos}\:\theta}{{m}}={g}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right) \\ $$$$\alpha=\frac{{fr}}{{I}}=\frac{\mu{mgr}\:\mathrm{cos}\:\theta}{\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{2}\mu{g}\:\mathrm{cos}\:\theta}{{r}} \\ $$$${v}_{\mathrm{1}} =\omega_{\mathrm{1}} {r} \\ $$$${t}_{\mathrm{1}} =\frac{{v}_{\mathrm{1}} }{{a}}=\frac{\omega_{\mathrm{1}} +\omega}{\alpha} \\ $$$$\frac{\omega_{\mathrm{1}} {r}}{{g}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)}=\frac{\left(\omega_{\mathrm{1}} +\omega\right){r}}{\mathrm{2}\mu{g}\:\mathrm{cos}\:\theta} \\ $$$$\frac{\omega_{\mathrm{1}} }{\mathrm{tan}\:\theta−\mu}=\frac{\omega_{\mathrm{1}} +\omega}{\mathrm{2}\mu} \\ $$$$\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)\omega_{\mathrm{1}} =\left(\mathrm{tan}\:\theta−\mu\right)\omega \\ $$$$\Rightarrow\omega_{\mathrm{1}} =\frac{\left(\mathrm{tan}\:\theta−\mu\right)\omega}{\mathrm{3}\mu−\mathrm{tan}\:\theta} \\ $$$$\frac{\mathrm{tan}\:\theta}{\mathrm{3}}<\mu<\mathrm{tan}\:\theta \\ $$$${s}=\frac{{v}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}{a}}=\frac{\left(\mathrm{tan}\:\theta−\mu\right)^{\mathrm{2}} \omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{s}=\frac{\left(\mathrm{tan}\:\theta−\mu\right)\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{3}\mu−\mathrm{tan}\:\theta\right)^{\mathrm{2}} \mathrm{cos}\:\theta} \\ $$$$ \\ $$$${if}\:\mu\leqslant\frac{\mathrm{tan}\:\theta}{\mathrm{3}},\:{the}\:{disc}\:{can}\:{never}\:{roll} \\ $$$${only}\:{on}\:{the}\:{incline},\:{but}\:{always}\:{roll} \\ $$$${and}\:{slip}. \\ $$

Commented by ajfour last updated on 15/Jan/25

https://youtu.be/-RRr7_nNNqI?si=mdeobU80KLO5c5m- A special case of a more general geometry question that mrW sir, MJS sir and myself had solved way back several yers.

Commented by mr W last updated on 15/Jan/25

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com