
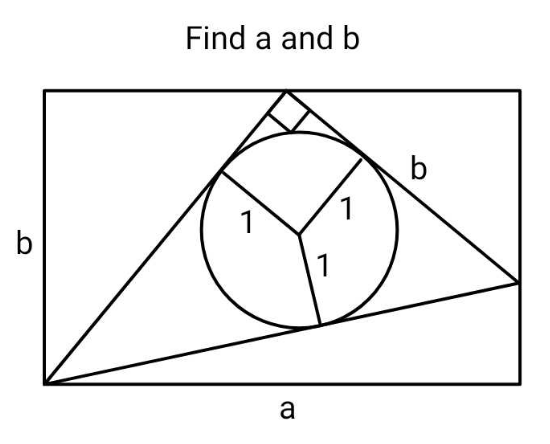
Question Number 215400 by ajfour last updated on 05/Jan/25
Commented by ajfour last updated on 05/Jan/25
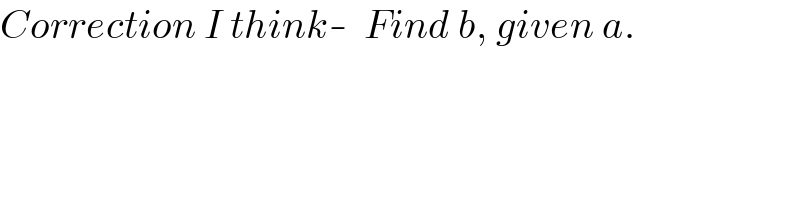
$${Correction}\:{I}\:{think}-\:\:{Find}\:{b},\:{given}\:{a}. \\ $$
Answered by mr W last updated on 06/Jan/25
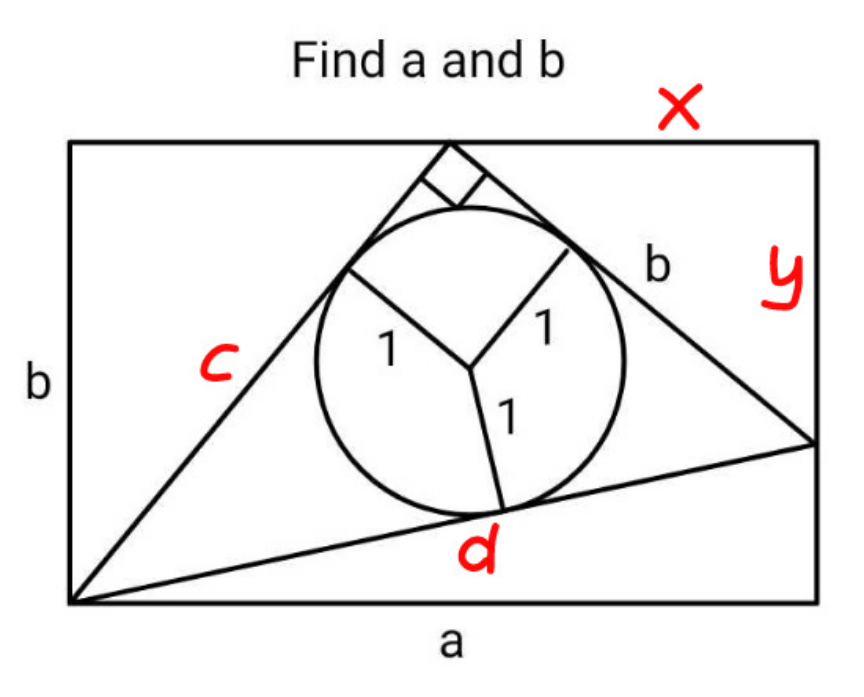
Commented by mr W last updated on 06/Jan/25
![r=1 α=(a/r), β=(b/r), γ=(c/γ) d=b−r+c−r=b+c−2r d^2 =b^2 +c^2 =b^2 +c^2 +4r^2 +2bc−4r(b+c) 2r^2 +bc−2r(b+c)=0 2+βγ−2(β+γ)=0 ⇒γ=((2(β−1))/(β−2)) x=a−(√(c^2 −b^2 )) y=b−(√(a^2 −d^2 ))=b−(√(a^2 −b^2 −c^2 )) [a−(√(c^2 −b^2 ))]^2 +[b−(√(a^2 −b^2 −c^2 ))]^2 =b^2 a^2 −b^2 =a(√(c^2 −b^2 ))+b(√(a^2 −b^2 −c^2 )) α(√(γ^2 −β^2 ))+β(√(α^2 −β^2 −γ^2 ))=α^2 −β^2 ⇒α(√(4(((β−1)/(β−2)))^2 −β^2 ))+β(√(α^2 −β^2 −4(((β−1)/(β−2)))^2 ))=α^2 −β^2](Q215423.png)
$${r}=\mathrm{1} \\ $$$$\alpha=\frac{{a}}{{r}},\:\beta=\frac{{b}}{{r}},\:\gamma=\frac{{c}}{\gamma} \\ $$$${d}={b}−{r}+{c}−{r}={b}+{c}−\mathrm{2}{r} \\ $$$${d}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} +\mathrm{2}{bc}−\mathrm{4}{r}\left({b}+{c}\right) \\ $$$$\mathrm{2}{r}^{\mathrm{2}} +{bc}−\mathrm{2}{r}\left({b}+{c}\right)=\mathrm{0} \\ $$$$\mathrm{2}+\beta\gamma−\mathrm{2}\left(\beta+\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\gamma=\frac{\mathrm{2}\left(\beta−\mathrm{1}\right)}{\beta−\mathrm{2}} \\ $$$${x}={a}−\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${y}={b}−\sqrt{{a}^{\mathrm{2}} −{d}^{\mathrm{2}} }={b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\left[{a}−\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right]^{\mathrm{2}} +\left[{b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }\right]^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={a}\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }+{b}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\alpha\sqrt{\gamma^{\mathrm{2}} −\beta^{\mathrm{2}} }+\beta\sqrt{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} −\gamma^{\mathrm{2}} }=\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \\ $$$$\Rightarrow\alpha\sqrt{\mathrm{4}\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)^{\mathrm{2}} −\beta^{\mathrm{2}} }+\beta\sqrt{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} −\mathrm{4}\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)^{\mathrm{2}} }=\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 06/Jan/25
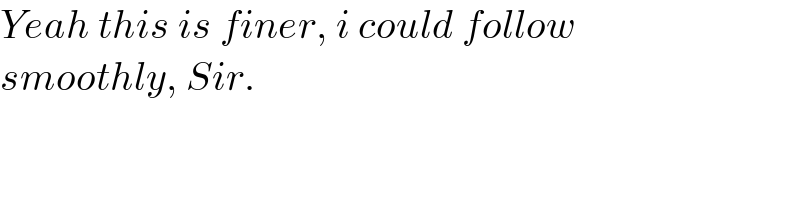
$${Yeah}\:{this}\:{is}\:{finer},\:{i}\:{could}\:{follow} \\ $$$${smoothly},\:{Sir}. \\ $$
Answered by ajfour last updated on 05/Jan/25
![I get underneath relation: [(√((((b−1)/((b/2)−1)))^2 −b^2 ))−a]^2 +[(√((((b−1)/((b/2)−1))+b−2)^2 −a^2 ))−b]^2 =a^2 +b^2](Q215402.png)
$${I}\:{get}\:{underneath}\:{relation}: \\ $$$$\left[\sqrt{\left(\frac{{b}−\mathrm{1}}{\frac{{b}}{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }−{a}\right]^{\mathrm{2}} +\left[\sqrt{\left(\frac{{b}−\mathrm{1}}{\frac{{b}}{\mathrm{2}}−\mathrm{1}}+{b}−\mathrm{2}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }−{b}\right]^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by mr W last updated on 05/Jan/25
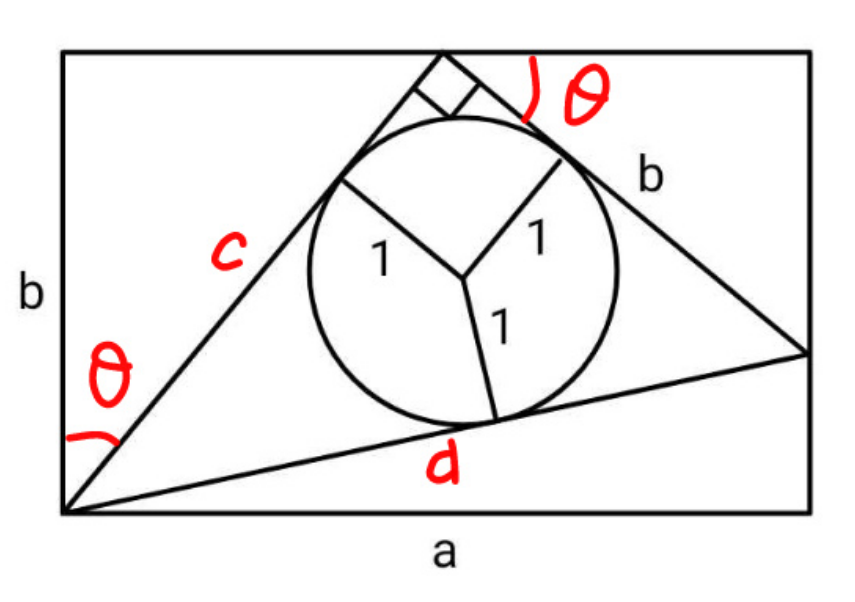
Commented by mr W last updated on 05/Jan/25
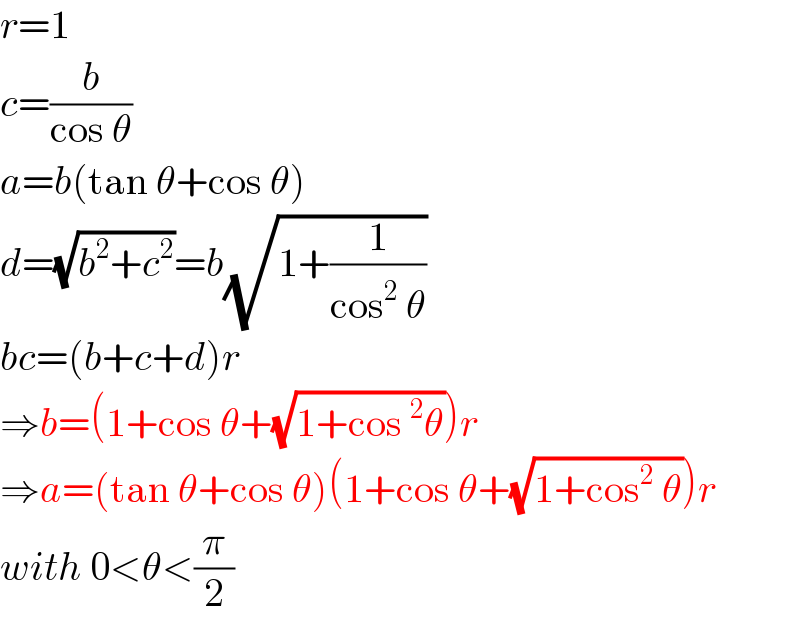
$${r}=\mathrm{1} \\ $$$${c}=\frac{{b}}{\mathrm{cos}\:\theta} \\ $$$${a}={b}\left(\mathrm{tan}\:\theta+\mathrm{cos}\:\theta\right) \\ $$$${d}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }={b}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$${bc}=\left({b}+{c}+{d}\right){r} \\ $$$$\Rightarrow{b}=\left(\mathrm{1}+\mathrm{cos}\:\theta+\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \theta}\right){r} \\ $$$$\Rightarrow{a}=\left(\mathrm{tan}\:\theta+\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{cos}\:\theta+\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}\right){r} \\ $$$${with}\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$
