
Question Number 215395 by mr W last updated on 05/Jan/25
Commented by mr W last updated on 06/Jan/25

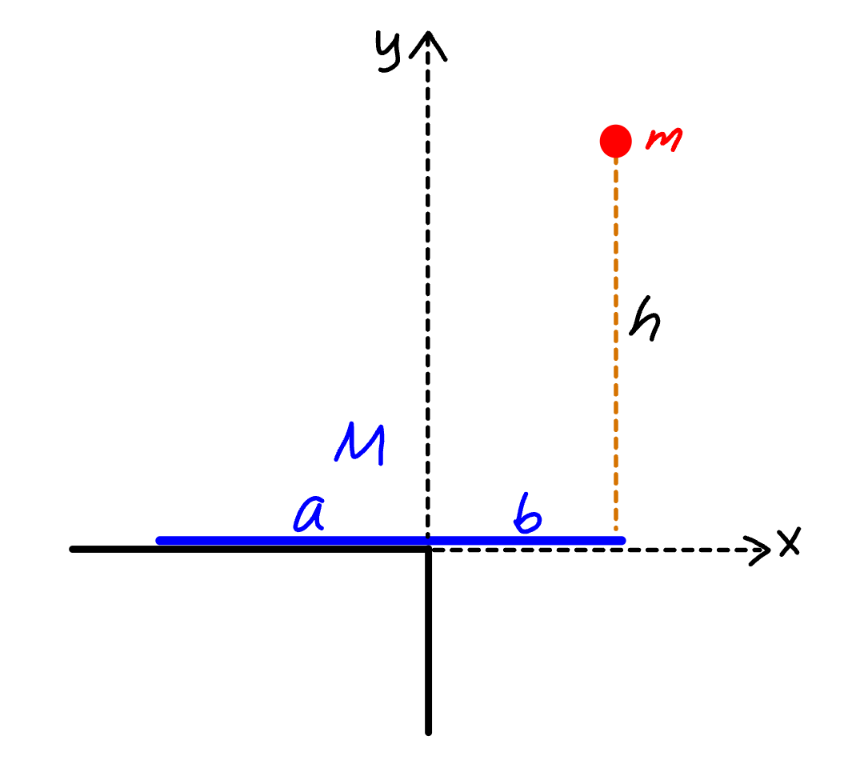
$${a}\:{ball}\:{with}\:{mass}\:{m}\:{falls}\:{from}\:{the} \\ $$$${hight}\:{h}\:{and}\:{hits}\:{the}\:{end}\:{of}\:{the}\:{rod} \\ $$$${jutting}\:{out}\:{off}\:{the}\:{edge}\:{of}\:{a}\:{table}. \\ $$$${the}\:{length}\:{of}\:{the}\:{uniform}\:{rod}\:{with}\: \\ $$$${mass}\:{M}\:{is}\:{L}={a}+{b}\:\left({a}>{b}\right). \\ $$$$ \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{maximum}\:{hight}\:{which} \\ $$$${the}\:{ball}\:{will}\:{reach}\:{after}\:{collision}. \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{maximum}\:{hight}\:{which} \\ $$$${the}\:{rod}\:{will}\:{reach}\:{after}\:{collision}. \\ $$$$\left({supposed}\:{that}\:{the}\:{table}\:{is}\:{removed}\right. \\ $$$${away}\:{after}\:{the}\:{collision}\:{so}\:{that}\:{the} \\ $$$$\left.{rod}\:{can}\:{move}\:{freely}\right). \\ $$
Commented by ajfour last updated on 07/Jan/25
https://youtu.be/2O_ZoICD2Ss?si=r85hss2CP8u60lv6 Motion of charge in variable magnetic field
Commented by mr W last updated on 07/Jan/25
��
Answered by mr W last updated on 07/Jan/25
Commented by mr W last updated on 10/Jan/25
Commented by mr W last updated on 10/Jan/25
![f=μN=μmg cos θ v=ωr I_p =((2mr^2 )/5)+mr^2 =((7mr^2 )/5) mg(sin θ+μcos θ)s_1 =((mu^2 )/2)−(1/2)×((7mr^2 ω^2 )/5) ⇒g(sin θ+μcos θ)s_1 =(u^2 /2)−((7r^2 ω^2 )/(10)) a=(sin θ+μ cos θ)g α=((fr)/I)=((μmgr cos θ)/((2mr^2 )/5))=((5μg cos θ)/(2r)) ((u−v)/a)=((u−rω)/((sin θ+μ cos θ)g))=(ω/α)=((2rω)/(5μg cos θ)) ((u−rω)/(tan θ+μ))=((2rω)/(5μ)) ⇒rω=((5μu)/(7μ+2 tan θ)) g(sin θ+μcos θ)s_1 =(u^2 /2)−(7/(10))×(((5μu)/(7μ+2 tan θ)))^2 s_1 =(([1−((35μ^2 )/((7μ+2 tan θ)^2 ))]u^2 )/(2g(sin θ+μ cos θ))) mgs_2 sin θ=(1/2)×((7mr^2 ω^2 )/5) s_2 =((7r^2 ω^2 )/(10g sin θ))=(7/(10g sin θ))×(((5μu)/(7μ+2 tan θ)))^2 ⇒s_2 =((35μ^2 u^2 )/(2g sin θ (7μ+2 tan θ)^2 )) s=s_1 +s_2 ⇒s=(([1+((35μ^2 )/((7μ+2 tan θ)^2 ))]u^2 )/(2g(sin θ+μ cos θ)))+((35μ^2 u^2 )/(2g sin θ (7μ+2 tan θ)^2 ))](Q215577.png)
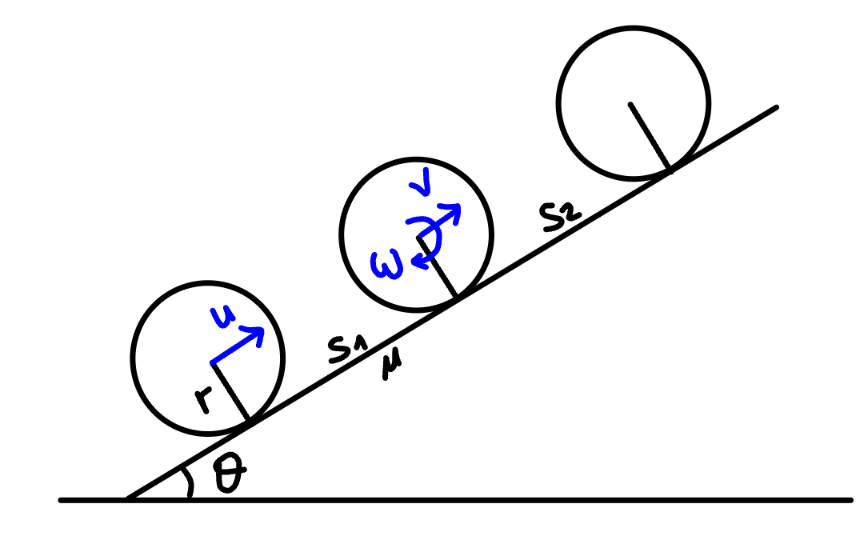
$${f}=\mu{N}=\mu{mg}\:\mathrm{cos}\:\theta \\ $$$${v}=\omega{r} \\ $$$${I}_{{p}} =\frac{\mathrm{2}{mr}^{\mathrm{2}} }{\mathrm{5}}+{mr}^{\mathrm{2}} =\frac{\mathrm{7}{mr}^{\mathrm{2}} }{\mathrm{5}} \\ $$$${mg}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right){s}_{\mathrm{1}} =\frac{{mu}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{7}{mr}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\Rightarrow{g}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right){s}_{\mathrm{1}} =\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}{r}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{10}} \\ $$$${a}=\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right){g} \\ $$$$\alpha=\frac{{fr}}{{I}}=\frac{\mu{mgr}\:\mathrm{cos}\:\theta}{\frac{\mathrm{2}{mr}^{\mathrm{2}} }{\mathrm{5}}}=\frac{\mathrm{5}\mu{g}\:\mathrm{cos}\:\theta}{\mathrm{2}{r}} \\ $$$$\frac{{u}−{v}}{{a}}=\frac{{u}−{r}\omega}{\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right){g}}=\frac{\omega}{\alpha}=\frac{\mathrm{2}{r}\omega}{\mathrm{5}\mu{g}\:\mathrm{cos}\:\theta} \\ $$$$\frac{{u}−{r}\omega}{\mathrm{tan}\:\theta+\mu}=\frac{\mathrm{2}{r}\omega}{\mathrm{5}\mu} \\ $$$$\Rightarrow{r}\omega=\frac{\mathrm{5}\mu{u}}{\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta} \\ $$$${g}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right){s}_{\mathrm{1}} =\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{10}}×\left(\frac{\mathrm{5}\mu{u}}{\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta}\right)^{\mathrm{2}} \\ $$$${s}_{\mathrm{1}} =\frac{\left[\mathrm{1}−\frac{\mathrm{35}\mu^{\mathrm{2}} }{\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }\right]{u}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right)} \\ $$$${mgs}_{\mathrm{2}} \mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{7}{mr}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{5}} \\ $$$${s}_{\mathrm{2}} =\frac{\mathrm{7}{r}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{10}{g}\:\mathrm{sin}\:\theta}=\frac{\mathrm{7}}{\mathrm{10}{g}\:\mathrm{sin}\:\theta}×\left(\frac{\mathrm{5}\mu{u}}{\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{s}_{\mathrm{2}} =\frac{\mathrm{35}\mu^{\mathrm{2}} {u}^{\mathrm{2}} }{\mathrm{2}{g}\:\mathrm{sin}\:\theta\:\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} } \\ $$$${s}={s}_{\mathrm{1}} +{s}_{\mathrm{2}} \\ $$$$\Rightarrow{s}=\frac{\left[\mathrm{1}+\frac{\mathrm{35}\mu^{\mathrm{2}} }{\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }\right]{u}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right)}+\frac{\mathrm{35}\mu^{\mathrm{2}} {u}^{\mathrm{2}} }{\mathrm{2}{g}\:\mathrm{sin}\:\theta\:\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 08/Jan/25
![u=(√(2gh)) mv=J_1 −mu V=(((a−b)ω)/2) MV=J_2 −J_1 ((M(a−b)ω)/2)=J_2 −m(v+u) J_2 =((M(a−b)ω)/2)+m(v+u) ((M(a+b)^2 ω)/(12))=J_1 b−(((a−b)J_2 )/2) ((M(a+b)^2 ω)/(12))=m(v+u)b−(((a−b))/2)[((M(a−b)ω)/2)+m(v+u)] (((a^2 +b^2 −ab)Mω)/3)=((m(3b−a)(v+u))/2) ⇒v=((2M(a^2 +b^2 −ab)ω)/(3m(3b−a)))−u ((m(u^2 −v^2 ))/2)=((MV^2 )/2)+(1/2)×((M(a+b)^2 ω^2 )/(12)) ((m(u^2 −v^2 ))/M)=(((a−b)^2 ω^2 )/4)+(((a+b)^2 ω^2 )/(12)) v^2 =u^2 −((M(a^2 +b^2 −ab)ω^2 )/(3m)) with μ=(m/M) [((2(a^2 +b^2 −ab)ω)/(3μ(3b−a)))−u]^2 =u^2 −(((a^2 +b^2 −ab)ω^2 )/(3μ)) ⇒ω=((12μ(3b−a)u)/(4(a^2 +b^2 −ab)+3μ(3b−a)^2 )) x_A =(((a+b)cos (ωt))/2) y_A =Vt−((gt^2 )/2)+(((a+b)sin (ωt))/2) y_A =(((a−b)ωt)/2)−((gt^2 )/2)+(((a+b)sin (ωt))/2) v=[(8/(4+((3μ(3b−a)^2 )/(a^2 +b^2 −ab))))−1]u v=0 when μ=((4(a^2 +b^2 −ab))/(3(3b−a)^2 )) for v>0, i.e. when the ball rebounds from the rod, it can reach a maximum hight h_(max) with (h_(max) /h)=((v/u))^2 =[(8/(4+((3μ(3b−a)^2 )/(a^2 +b^2 −ab))))−1]^2 with (b/a)=λ (h_(max) /h)=[(8/(4+((3μ(3λ−1)^2 )/(λ^2 −λ+1))))−1]^2](Q215490.png)
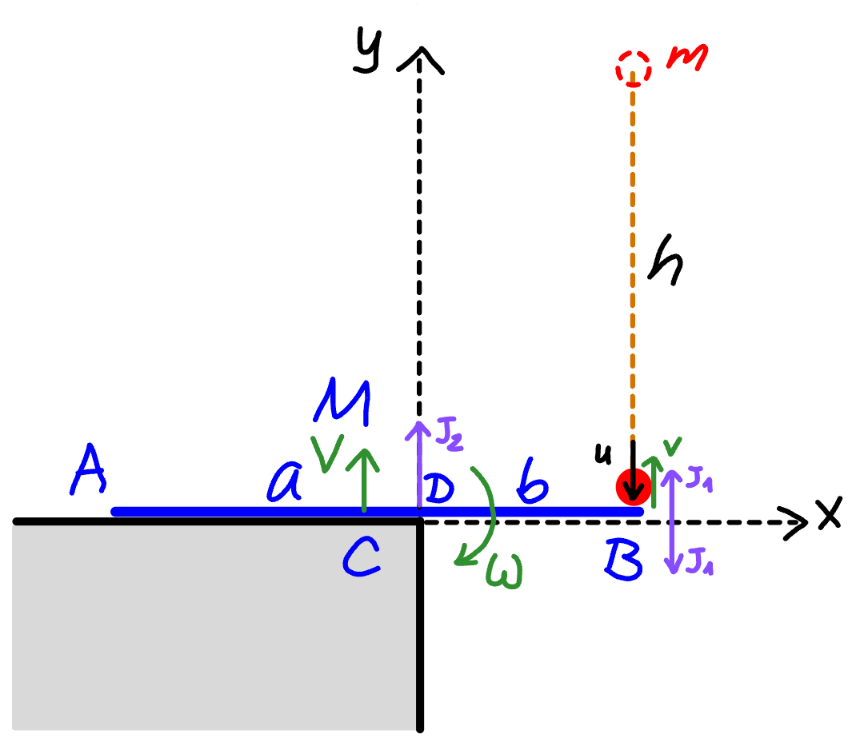
$${u}=\sqrt{\mathrm{2}{gh}} \\ $$$${mv}={J}_{\mathrm{1}} −{mu} \\ $$$${V}=\frac{\left({a}−{b}\right)\omega}{\mathrm{2}} \\ $$$${MV}={J}_{\mathrm{2}} −{J}_{\mathrm{1}} \\ $$$$\frac{{M}\left({a}−{b}\right)\omega}{\mathrm{2}}={J}_{\mathrm{2}} −{m}\left({v}+{u}\right) \\ $$$${J}_{\mathrm{2}} =\frac{{M}\left({a}−{b}\right)\omega}{\mathrm{2}}+{m}\left({v}+{u}\right) \\ $$$$\frac{{M}\left({a}+{b}\right)^{\mathrm{2}} \omega}{\mathrm{12}}={J}_{\mathrm{1}} {b}−\frac{\left({a}−{b}\right){J}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{M}\left({a}+{b}\right)^{\mathrm{2}} \omega}{\mathrm{12}}={m}\left({v}+{u}\right){b}−\frac{\left({a}−{b}\right)}{\mathrm{2}}\left[\frac{{M}\left({a}−{b}\right)\omega}{\mathrm{2}}+{m}\left({v}+{u}\right)\right] \\ $$$$\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right){M}\omega}{\mathrm{3}}=\frac{{m}\left(\mathrm{3}{b}−{a}\right)\left({v}+{u}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}{M}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)\omega}{\mathrm{3}{m}\left(\mathrm{3}{b}−{a}\right)}−{u} \\ $$$$\frac{{m}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)}{\mathrm{2}}=\frac{{MV}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{M}\left({a}+{b}\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\frac{{m}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)}{{M}}=\frac{\left({a}−{b}\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}}+\frac{\left({a}+{b}\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}} \\ $$$${v}^{\mathrm{2}} ={u}^{\mathrm{2}} −\frac{{M}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)\omega^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${with}\:\mu=\frac{{m}}{{M}} \\ $$$$\left[\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)\omega}{\mathrm{3}\mu\left(\mathrm{3}{b}−{a}\right)}−{u}\right]^{\mathrm{2}} ={u}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)\omega^{\mathrm{2}} }{\mathrm{3}\mu} \\ $$$$\Rightarrow\omega=\frac{\mathrm{12}\mu\left(\mathrm{3}{b}−{a}\right){u}}{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)+\mathrm{3}\mu\left(\mathrm{3}{b}−{a}\right)^{\mathrm{2}} } \\ $$$${x}_{{A}} =\frac{\left({a}+{b}\right)\mathrm{cos}\:\left(\omega{t}\right)}{\mathrm{2}} \\ $$$${y}_{{A}} ={Vt}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}+\frac{\left({a}+{b}\right)\mathrm{sin}\:\left(\omega{t}\right)}{\mathrm{2}} \\ $$$${y}_{{A}} =\frac{\left({a}−{b}\right)\omega{t}}{\mathrm{2}}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}+\frac{\left({a}+{b}\right)\mathrm{sin}\:\left(\omega{t}\right)}{\mathrm{2}} \\ $$$${v}=\left[\frac{\mathrm{8}}{\mathrm{4}+\frac{\mathrm{3}\mu\left(\mathrm{3}{b}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}}}−\mathrm{1}\right]{u} \\ $$$${v}=\mathrm{0}\:{when}\:\mu=\frac{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)}{\mathrm{3}\left(\mathrm{3}{b}−{a}\right)^{\mathrm{2}} } \\ $$$${for}\:{v}>\mathrm{0},\:{i}.{e}.\:{when}\:{the}\:{ball}\:{rebounds} \\ $$$${from}\:{the}\:{rod},\:{it}\:{can}\:{reach}\:{a}\:{maximum} \\ $$$${hight}\:{h}_{{max}} \:{with} \\ $$$$\frac{{h}_{{max}} }{{h}}=\left(\frac{{v}}{{u}}\right)^{\mathrm{2}} =\left[\frac{\mathrm{8}}{\mathrm{4}+\frac{\mathrm{3}\mu\left(\mathrm{3}{b}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}}}−\mathrm{1}\right]^{\mathrm{2}} \\ $$$${with}\:\frac{{b}}{{a}}=\lambda \\ $$$$\frac{{h}_{{max}} }{{h}}=\left[\frac{\mathrm{8}}{\mathrm{4}+\frac{\mathrm{3}\mu\left(\mathrm{3}\lambda−\mathrm{1}\right)^{\mathrm{2}} }{\lambda^{\mathrm{2}} −\lambda+\mathrm{1}}}−\mathrm{1}\right]^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 08/Jan/25
https://youtu.be/3wiUgK_riz8?si=pKPRqyotoxf-pwhm How far up the incline does solid ball reach?
Commented by mr W last updated on 08/Jan/25
��
Commented by mr W last updated on 09/Jan/25
Commented by mr W last updated on 09/Jan/25
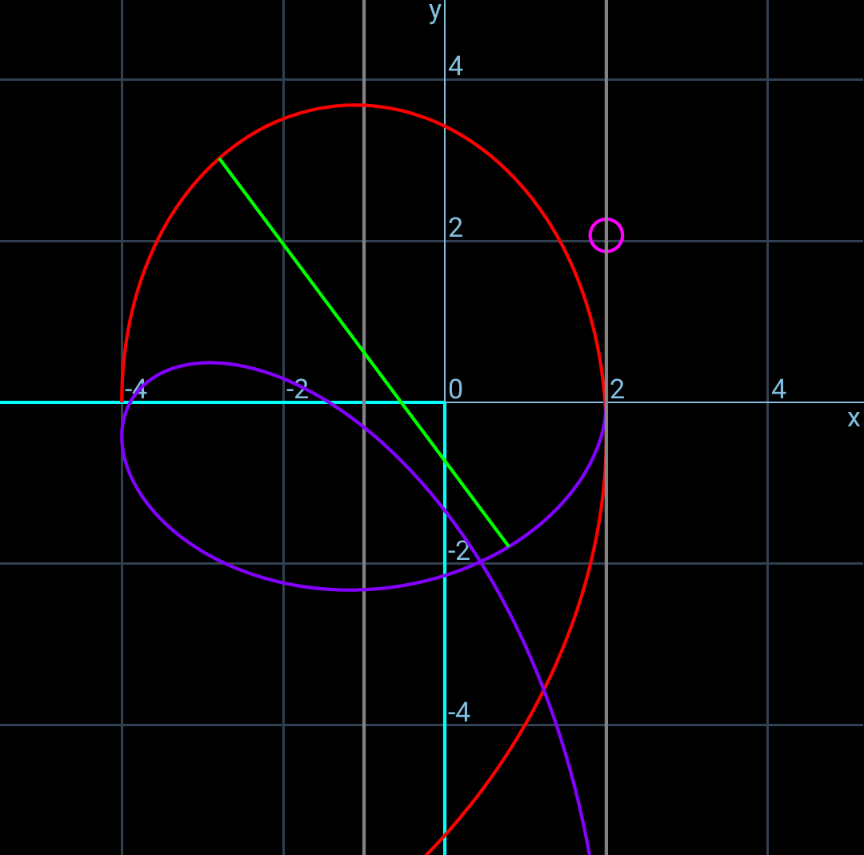
Commented by mr W last updated on 09/Jan/25
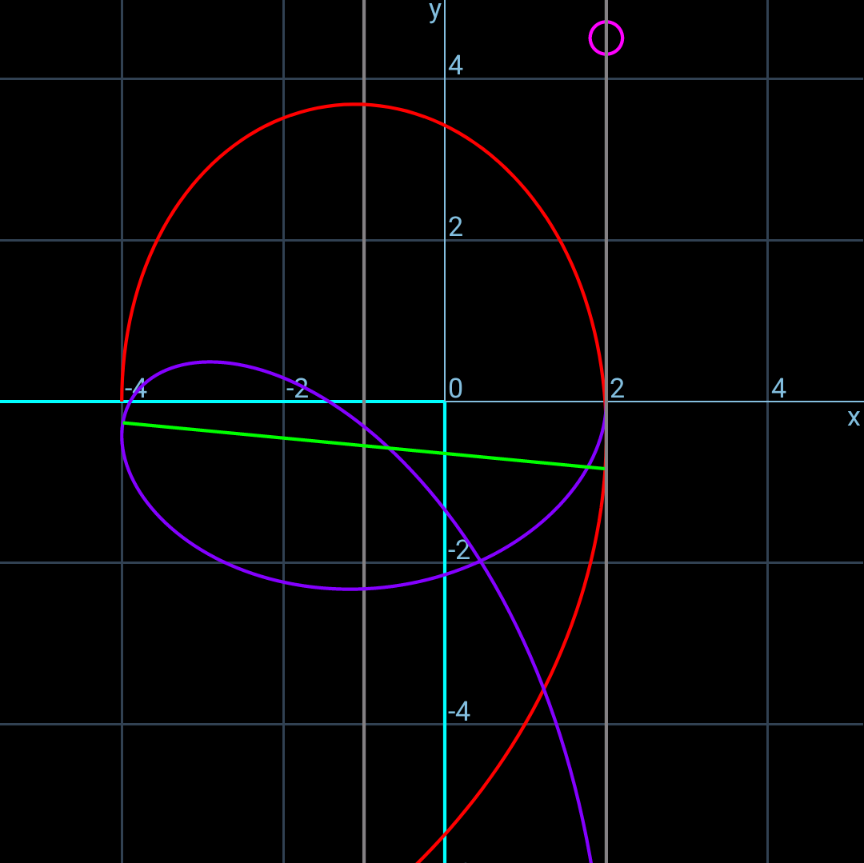
Commented by mr W last updated on 09/Jan/25
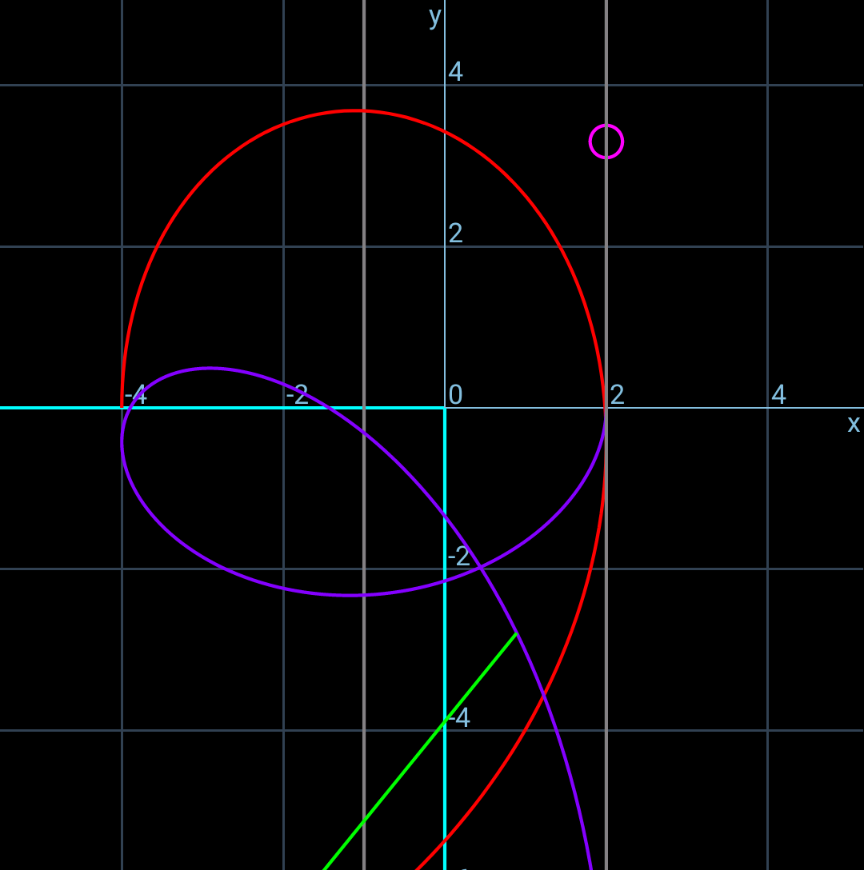
Commented by ajfour last updated on 10/Jan/25
Thanks for this. by the way any error/blunder in my video lecture for this question sir, did you notice?
Commented by mr W last updated on 10/Jan/25
![i got x=s_1 =(([1−((35μ^2 )/((7μ+2 tan θ)^2 ))]u^2 )/(2g(sin θ+μ cos θ))) while you got x=(([1−((25μ^2 )/((7μ+2 tan θ)^2 ))]u^2 )/(2g(sin θ+μ cos θ)))](Q215579.png)
$${i}\:{got}\:{x}={s}_{\mathrm{1}} =\frac{\left[\mathrm{1}−\frac{\mathrm{35}\mu^{\mathrm{2}} }{\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }\right]{u}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right)} \\ $$$${while}\:{you}\:{got} \\ $$$${x}=\frac{\left[\mathrm{1}−\frac{\mathrm{25}\mu^{\mathrm{2}} }{\left(\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }\right]{u}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right)} \\ $$
Commented by ajfour last updated on 11/Jan/25
![⇒g(sin θ+μcos θ)s_1 =(u^2 /2)−((7r^2 ω^2 )/(10)) Point of application of friction force moves through s_1 −r𝛗 so above eq. should be: g(sin θ)s_1 +(μgcos θ)(s_1 −r𝛗)=(u^2 /2)−((7r^2 ω^2 )/(10)) i mean incline sees sphere surface has rubbed past this length = s_1 −r𝛗 (v^2 /r^2 )=ω^2 =2(((μmgrcos θ)/((2/5)mr^2 )))𝛗 (v^2 /r^2 )=ω^2 =(((5μg)/r)cos θ)φ μrg𝛗cos θ=(v^2 /5)=((ω^2 r^2 )/5) hence s_1 (sin θ+μcos θ)g−((2ω^2 r^2 )/(10))=(u^2 /2)−((7ω^2 r^2 )/(10)) s_1 =((u^2 −ω^2 r^2 )/(2g(sin θ+μcos θ))) now as rω=((5μu)/(7μ+2 tan θ)) s_1 =(([1−((25μ^2 )/((7μ+2tan θ)^2 ))]u^2 )/(2g(sin θ+μcos θ))) ★ Along this approach i would get this, sir!](Q215594.png)
$$\Rightarrow{g}\left(\mathrm{sin}\:\theta+\underline{\mu\mathrm{cos}\:\theta}\right){s}_{\mathrm{1}} =\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}{r}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{10}} \\ $$$${Point}\:{of}\:{application}\:{of}\:{friction}\:{force}\:{moves} \\ $$$${through}\:{s}_{\mathrm{1}} −{r}\boldsymbol{\phi}\:\:{so}\:\:{above}\:{eq}.\:{should}\:{be}: \\ $$$${g}\left(\mathrm{sin}\:\theta\right){s}_{\mathrm{1}} +\left(\mu{g}\mathrm{cos}\:\theta\right)\left({s}_{\mathrm{1}} −{r}\boldsymbol{\phi}\right)=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}{r}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{10}} \\ $$$${i}\:{mean}\:{incline}\:{sees}\:{sphere}\:{surface}\: \\ $$$${has}\:{rubbed}\:{past}\:{this}\:{length}\:=\:{s}_{\mathrm{1}} −{r}\boldsymbol{\phi} \\ $$$$\frac{{v}^{\mathrm{2}} }{{r}^{\mathrm{2}} }=\omega^{\mathrm{2}} =\mathrm{2}\left(\frac{\mu{mgr}\mathrm{cos}\:\theta}{\frac{\mathrm{2}}{\mathrm{5}}{mr}^{\mathrm{2}} }\right)\boldsymbol{\phi} \\ $$$$\frac{{v}^{\mathrm{2}} }{{r}^{\mathrm{2}} }=\omega^{\mathrm{2}} =\left(\frac{\mathrm{5}\mu{g}}{{r}}\mathrm{cos}\:\theta\right)\phi \\ $$$$\mu{rg}\boldsymbol{\phi}\mathrm{cos}\:\theta=\frac{{v}^{\mathrm{2}} }{\mathrm{5}}=\frac{\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{5}}\:\:\:\:\:\:\:\:{hence} \\ $$$${s}_{\mathrm{1}} \left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right){g}−\frac{\mathrm{2}\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{10}}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{10}} \\ $$$${s}_{\mathrm{1}} =\frac{{u}^{\mathrm{2}} −\omega^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)} \\ $$$${now}\:\:{as}\:\:{r}\omega=\frac{\mathrm{5}\mu{u}}{\mathrm{7}\mu+\mathrm{2}\:\mathrm{tan}\:\theta} \\ $$$${s}_{\mathrm{1}} =\frac{\left[\mathrm{1}−\frac{\mathrm{25}\mu^{\mathrm{2}} }{\left(\mathrm{7}\mu+\mathrm{2tan}\:\theta\right)^{\mathrm{2}} }\right]{u}^{\mathrm{2}} }{\mathrm{2}{g}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)}\:\:\:\bigstar \\ $$$${Along}\:{this}\:{approach}\:{i}\:{would}\:{get}\:{this},\:{sir}! \\ $$
Commented by mr W last updated on 11/Jan/25
$${you}\:{are}\:{right}\:{sir},\:{thanks}\:{alot}! \\ $$
