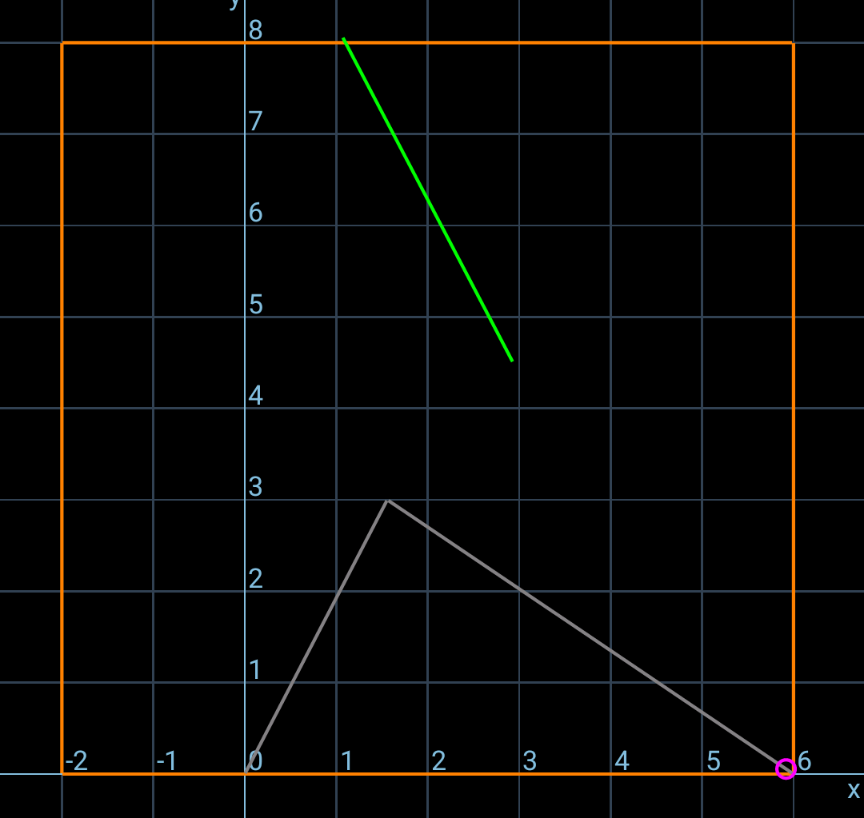
Question Number 215312 by ajfour last updated on 02/Jan/25
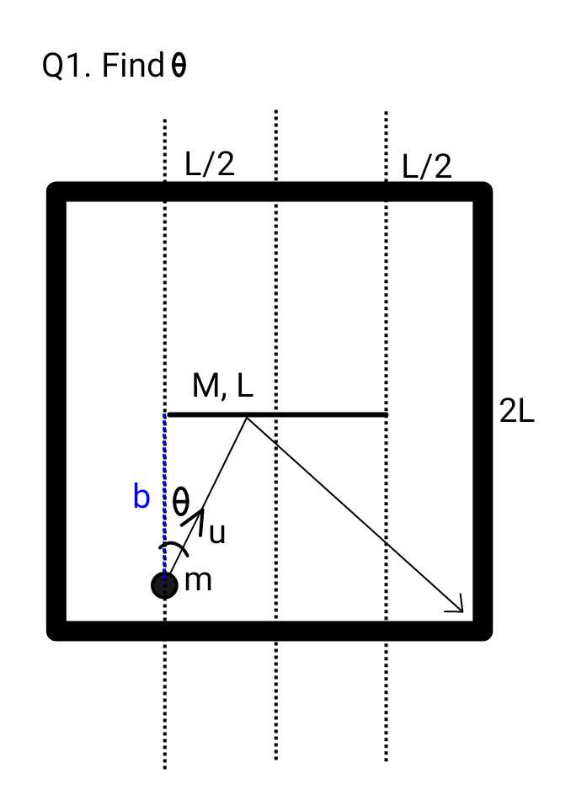
Commented by mr W last updated on 06/Jan/25

$${please}\:{try}\:{Q}\mathrm{215395} \\ $$
Answered by mr W last updated on 03/Jan/25
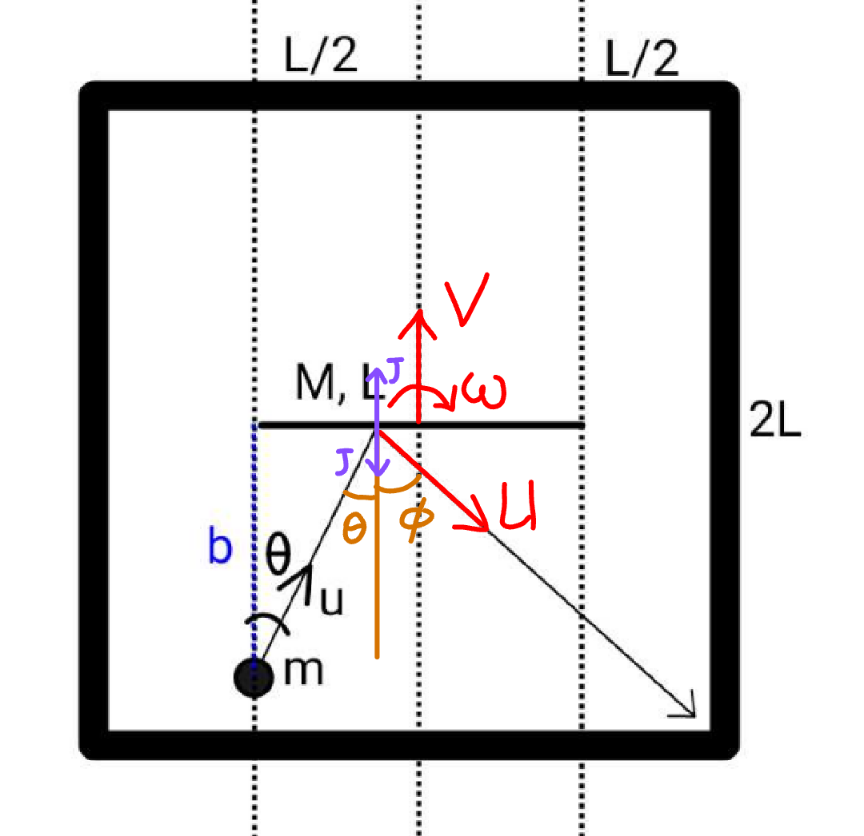
Commented by mr W last updated on 03/Jan/25
![I=((ML^2 )/(12)) b(tan θ+tan φ)=((3L)/2) ⇒tan φ=((3L)/(2b))−tan θ mu sin θ=mU sin φ ⇒U=((u sin θ)/(sin φ)) mu cos θ−J=mU cos φ ⇒J=mu(cos θ−((sin θ)/(tan φ))) MV=J ⇒V=((mu)/(M(cos θ−((sin θ)/(tan φ))))) ((ML^2 ω)/(12))=J((L/2)−b tan θ) ⇒ω=((12mu((1/2)−((b tan θ)/L)))/(ML(cos θ−((sin θ)/(tan φ))))) ((mU^2 )/2)+((MV^2 )/2)+(1/2)×((ML^2 ω^2 )/(12))=((mu^2 )/2) ((sin^2 θ)/(sin^2 φ))+(m/(M(cos θ−((sin θ)/(tan φ)))^2 ))+((12m((1/2)−((b tan θ)/L))^2 )/(M(cos θ−((sin θ)/(tan φ)))^2 ))=1 ((μ[1+12((1/2)−((b tan θ)/L))^2 ])/((cos θ−((sin θ)/(tan φ)))^2 ))=1−((sin^2 θ)/(sin^2 φ)) with μ=(m/M), ξ=(b/L) ⇒((μ[1+12((1/2)−ξ tan θ)^2 ](1+tan^2 θ)^2 )/((1−((tan θ)/(tan φ)))^2 ))+(((tan θ)/(tan φ)))^2 =1 with tan φ=(3/(2ξ))−tan θ ================== θ_1 =ωt=((12μ((1/2)−ξ tan θ)ut)/(L(cos θ−((sin θ)/(tan φ))))) x_1 =(L/2) y_1 =b+Vt=ξL+((μut)/(cos θ−((sin θ)/(tan φ)))) x_2 =b tan θ+Ut sin φ=ξL tan θ+ut sin θ y_2 =b−Ut cos φ=ξL−((ut sin θ)/(tan φ))](Q215333.png)
$${I}=\frac{{ML}^{\mathrm{2}} }{\mathrm{12}} \\ $$$${b}\left(\mathrm{tan}\:\theta+\mathrm{tan}\:\phi\right)=\frac{\mathrm{3}{L}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\phi=\frac{\mathrm{3}{L}}{\mathrm{2}{b}}−\mathrm{tan}\:\theta \\ $$$${mu}\:\mathrm{sin}\:\theta={mU}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow{U}=\frac{{u}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\phi} \\ $$$${mu}\:\mathrm{cos}\:\theta−{J}={mU}\:\mathrm{cos}\:\phi \\ $$$$\Rightarrow{J}={mu}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right) \\ $$$${MV}={J} \\ $$$$\Rightarrow{V}=\frac{{mu}}{{M}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)} \\ $$$$\frac{{ML}^{\mathrm{2}} \omega}{\mathrm{12}}={J}\left(\frac{{L}}{\mathrm{2}}−{b}\:\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow\omega=\frac{\mathrm{12}{mu}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{b}\:\mathrm{tan}\:\theta}{{L}}\right)}{{ML}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)} \\ $$$$\frac{{mU}^{\mathrm{2}} }{\mathrm{2}}+\frac{{MV}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{ML}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{12}}=\frac{{mu}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi}+\frac{{m}}{{M}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }+\frac{\mathrm{12}{m}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{b}\:\mathrm{tan}\:\theta}{{L}}\right)^{\mathrm{2}} }{{M}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mu\left[\mathrm{1}+\mathrm{12}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{b}\:\mathrm{tan}\:\theta}{{L}}\right)^{\mathrm{2}} \right]}{\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi} \\ $$$${with}\:\mu=\frac{{m}}{{M}},\:\xi=\frac{{b}}{{L}} \\ $$$$\Rightarrow\frac{\mu\left[\mathrm{1}+\mathrm{12}\left(\frac{\mathrm{1}}{\mathrm{2}}−\xi\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} \right]\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }{\left(\mathrm{1}−\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }+\left(\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${with}\:\mathrm{tan}\:\phi=\frac{\mathrm{3}}{\mathrm{2}\xi}−\mathrm{tan}\:\theta \\ $$$$================== \\ $$$$\theta_{\mathrm{1}} =\omega{t}=\frac{\mathrm{12}\mu\left(\frac{\mathrm{1}}{\mathrm{2}}−\xi\:\mathrm{tan}\:\theta\right){ut}}{{L}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)} \\ $$$${x}_{\mathrm{1}} =\frac{{L}}{\mathrm{2}} \\ $$$${y}_{\mathrm{1}} ={b}+{Vt}=\xi{L}+\frac{\mu{ut}}{\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}} \\ $$$${x}_{\mathrm{2}} ={b}\:\mathrm{tan}\:\theta+{Ut}\:\mathrm{sin}\:\phi=\xi{L}\:\mathrm{tan}\:\theta+{ut}\:\mathrm{sin}\:\theta \\ $$$${y}_{\mathrm{2}} ={b}−{Ut}\:\mathrm{cos}\:\phi=\xi{L}−\frac{{ut}\:\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi} \\ $$
Commented by mr W last updated on 03/Jan/25
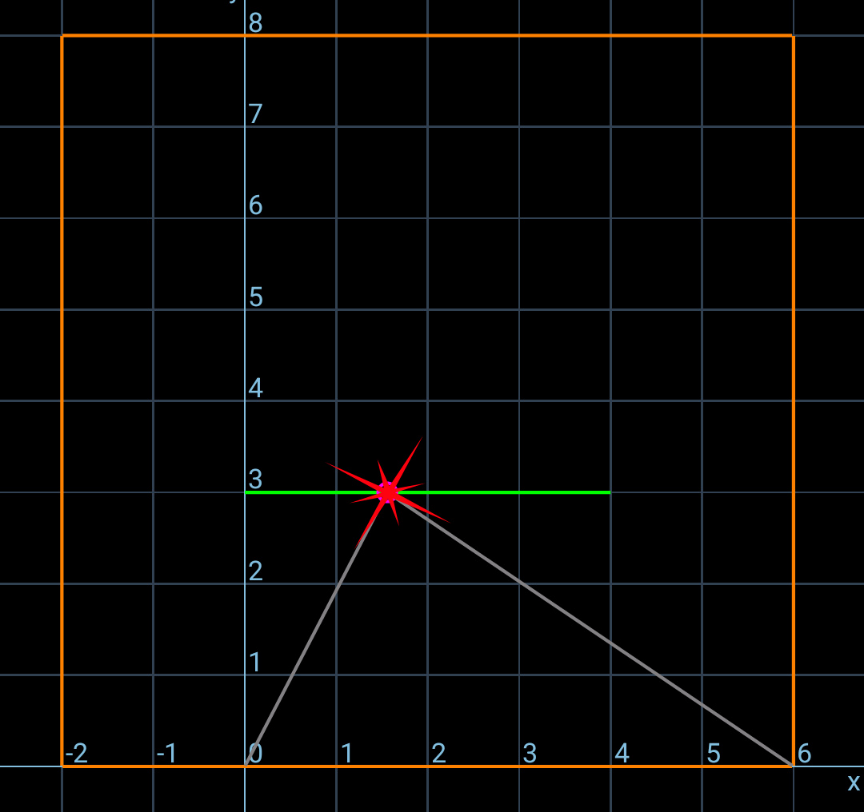
Commented by mr W last updated on 03/Jan/25
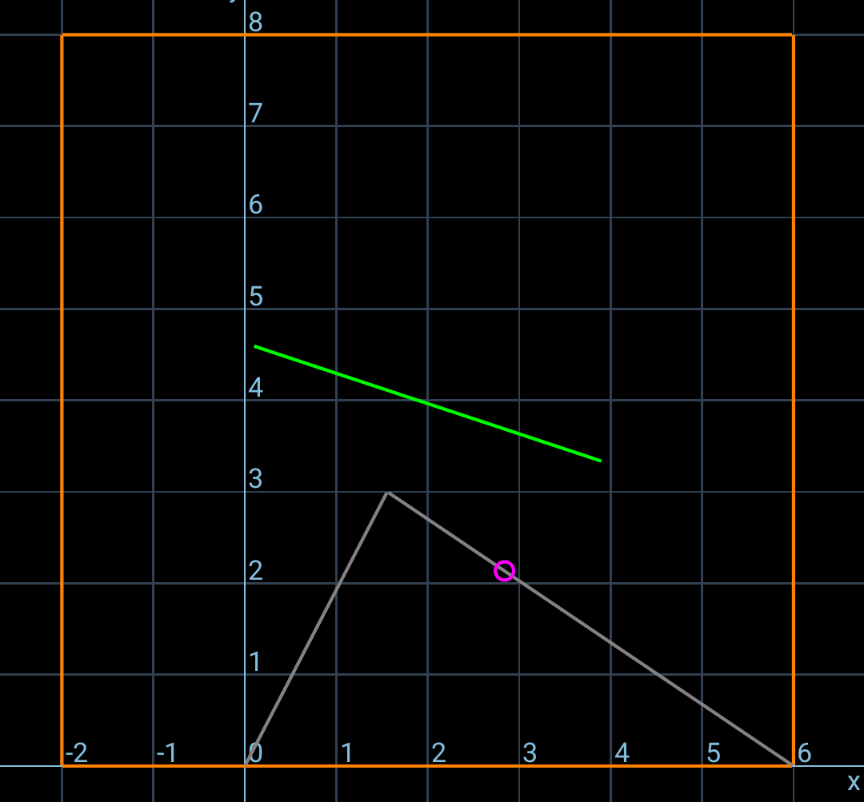
Commented by mr W last updated on 03/Jan/25
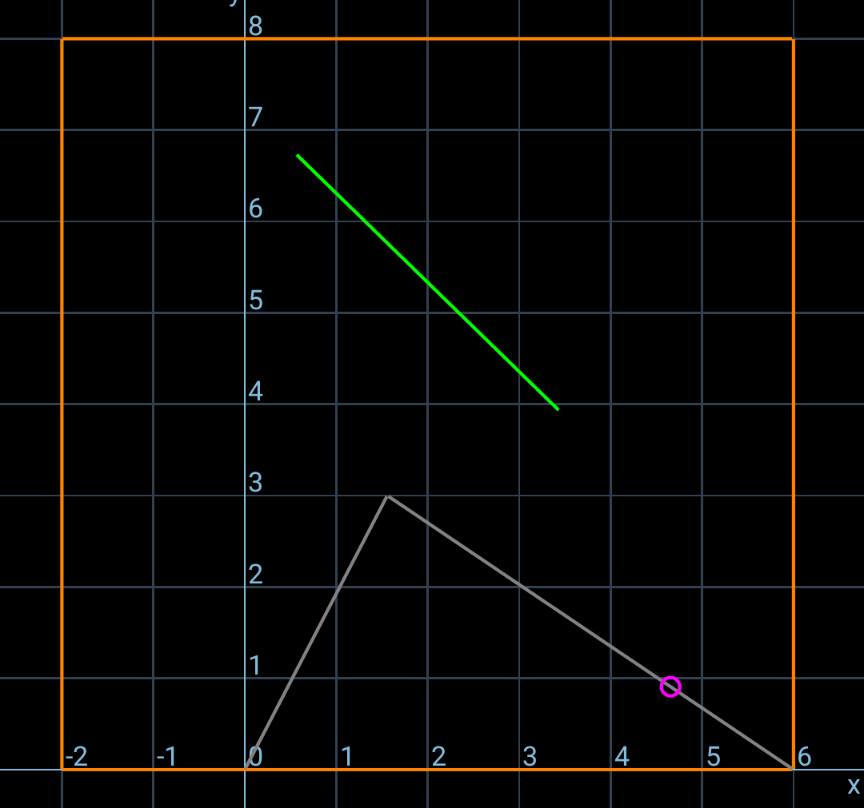
Commented by mr W last updated on 03/Jan/25