
Question Number 215256 by ajfour last updated on 01/Jan/25
Commented by ajfour last updated on 01/Jan/25

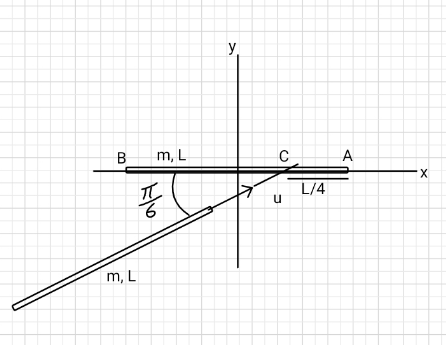
$${After}\:{this}\:{elastic}\:{collision}\:{on}\:{a}\:{flat} \\ $$$${frictionless}\:{surface}\:{Find}\:{after}\:{what} \\ $$$${time}\:{at}\:{what}\:{y}\:{coordinate}\:{does}\:{point} \\ $$$${A}\:{cross}\:{the}\:{y}-{axis}. \\ $$
Commented by ajfour last updated on 02/Jan/25
https://youtu.be/roXqnV-fZ7k?si=JafblceCGUAmx3u- My video lecture discussing a problem of finding spring extension when to each end of it is attached a positive charge q.
Answered by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
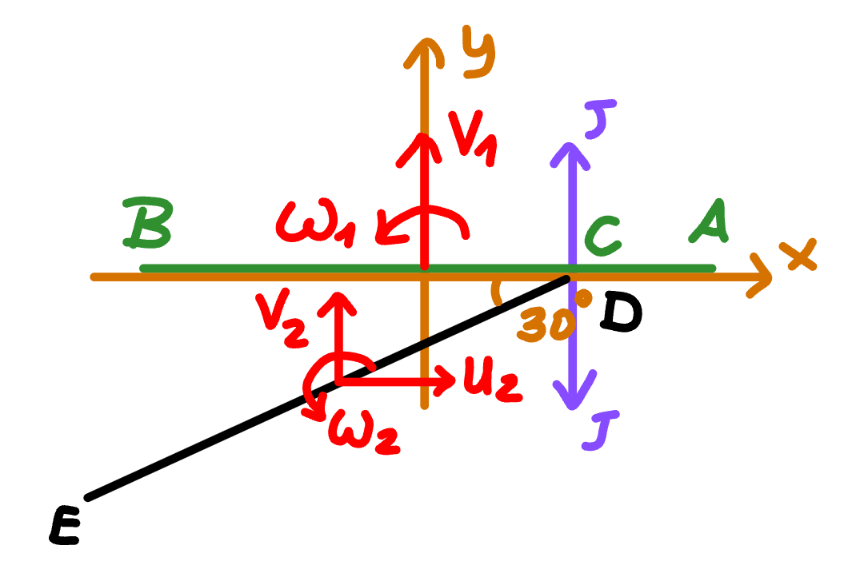
![I_1 =I_2 =((mL^2 )/(12)) mv_1 =J I_1 ω_1 =((JL)/4) ⇒ω_1 =((3v_1 )/L) mu_2 =mu cos 30° ⇒u_2 =(((√3)u)/2) mv_2 =mu sin 30°−J ⇒v_2 =(u/2)−v_1 I_2 ω_2 =−J×((L cos 30°)/2) ⇒ω_2 =−((3(√3)v_1 )/L) (m/2)(v_1 ^2 +u_2 ^2 +v_2 ^2 )+(1/2)×((mL^2 )/(12))(ω_1 ^2 +ω_2 ^2 )=((mu^2 )/2) v_1 ^2 +((((√3)u)/2))^2 +((u/2)−v_1 )^2 +(L^2 /(12))[(((3v_1 )/L))^2 +(−((3(√3)v_1 )/L))^2 ]=u^2 5v_1 ^2 −uv_1 =0 ⇒v_1 =(u/5) ⇒ω_1 =((3u)/(5L)) at time t point A crosses the y−axis: x_A =(L/2)cos (ω_1 t)=0 ⇒ω_1 t=((3ut)/(5L))=(π/2) ⇒t=((5πL)/(6u)) ✓ y_A =v_1 t+(L/2) sin (ω_1 t)=((Lω_1 t)/3)+(L/2) sin (ω_1 t) =(L/2)((π/3)+1) >L ================== θ_1 =ω_1 t=((3ut)/(5L)) x_1 =0 y_1 =v_1 t=((ut)/5) x_A =x_1 +((L cos θ_1 )/2)=((L cos (((3ut)/(5L))))/2) y_A =y_1 +((L sin θ_1 )/2)=((ut)/5)+((L sin (((3ut)/(5L))))/2) θ_2 =(π/6)+ω_2 t=(π/6)−((3(√3)ut)/(5L)) x_2 =(L/4)−(((√3)L)/4)+u_2 t=(((1−(√3))L)/4)+(((√3)ut)/2) y_2 =−(L/4)+v_2 t=−(L/4)+((3ut)/(10)) x_D =x_2 +((L cos θ_2 )/2)=(((1−(√3))L)/4)+(((√3)ut)/2)+((L cos ((π/6)−((3(√3)ut)/(5L))))/2) y_D =y_2 +((L sin θ_2 )/2)=−(L/4)+((3ut)/(10))+((L sin ((π/6)−((3(√3)ut)/(5L))))/2) ================== following pictures are showing the movement of the rods after the collision as well as the locus of the points A and D.](Q215278.png)
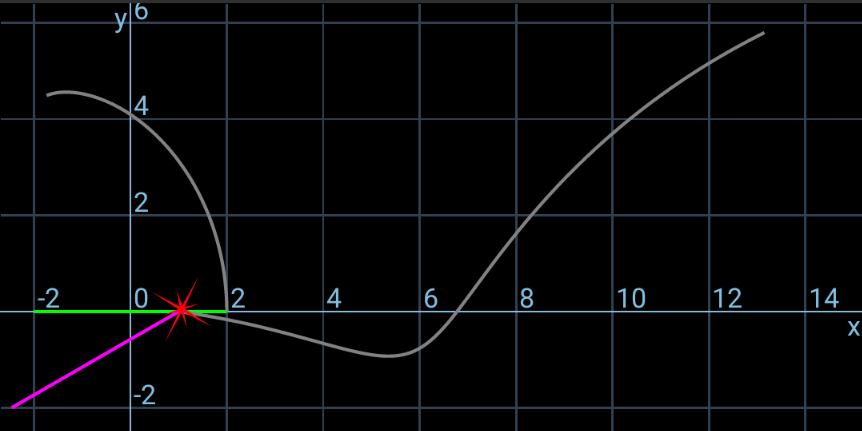
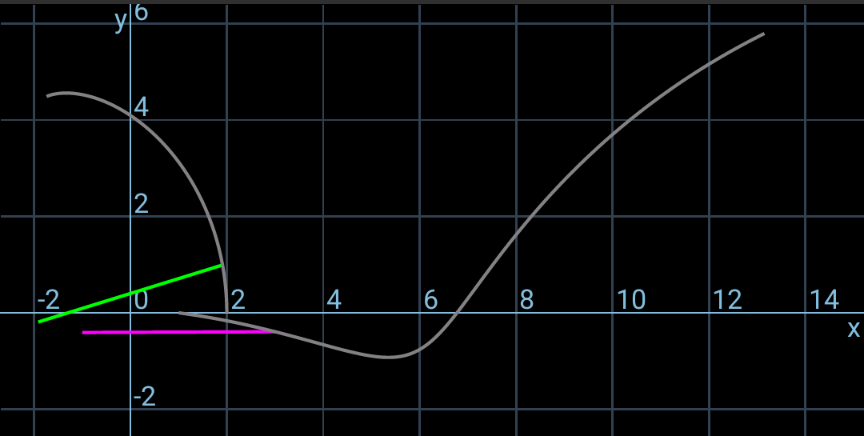
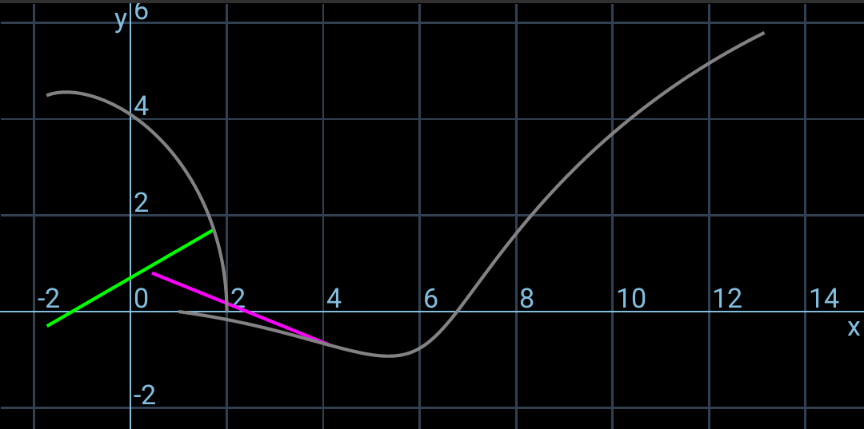
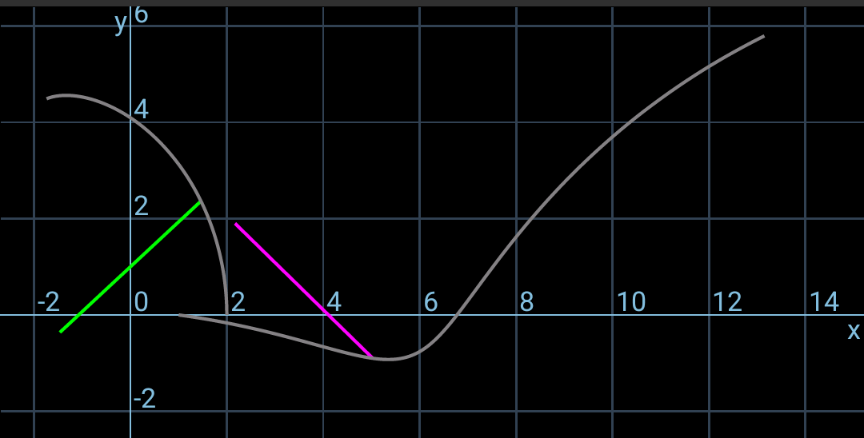
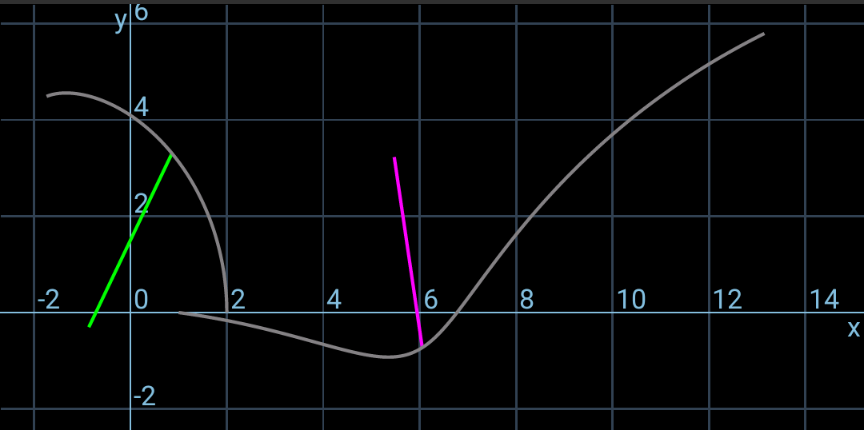
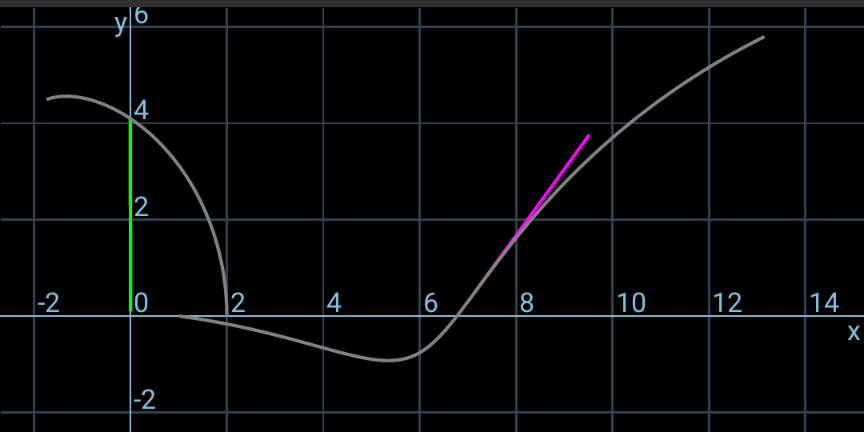
$${I}_{\mathrm{1}} ={I}_{\mathrm{2}} =\frac{{mL}^{\mathrm{2}} }{\mathrm{12}} \\ $$$${mv}_{\mathrm{1}} ={J} \\ $$$${I}_{\mathrm{1}} \omega_{\mathrm{1}} =\frac{{JL}}{\mathrm{4}} \\ $$$$\Rightarrow\omega_{\mathrm{1}} =\frac{\mathrm{3}{v}_{\mathrm{1}} }{{L}} \\ $$$${mu}_{\mathrm{2}} ={mu}\:\mathrm{cos}\:\mathrm{30}° \\ $$$$\Rightarrow{u}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}{u}}{\mathrm{2}} \\ $$$${mv}_{\mathrm{2}} ={mu}\:\mathrm{sin}\:\mathrm{30}°−{J} \\ $$$$\Rightarrow{v}_{\mathrm{2}} =\frac{{u}}{\mathrm{2}}−{v}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} \omega_{\mathrm{2}} =−{J}×\frac{{L}\:\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}} \\ $$$$\Rightarrow\omega_{\mathrm{2}} =−\frac{\mathrm{3}\sqrt{\mathrm{3}}{v}_{\mathrm{1}} }{{L}} \\ $$$$\frac{{m}}{\mathrm{2}}\left({v}_{\mathrm{1}} ^{\mathrm{2}} +{u}_{\mathrm{2}} ^{\mathrm{2}} +{v}_{\mathrm{2}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}\left(\omega_{\mathrm{1}} ^{\mathrm{2}} +\omega_{\mathrm{2}} ^{\mathrm{2}} \right)=\frac{{mu}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${v}_{\mathrm{1}} ^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{u}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{u}}{\mathrm{2}}−{v}_{\mathrm{1}} \right)^{\mathrm{2}} +\frac{{L}^{\mathrm{2}} }{\mathrm{12}}\left[\left(\frac{\mathrm{3}{v}_{\mathrm{1}} }{{L}}\right)^{\mathrm{2}} +\left(−\frac{\mathrm{3}\sqrt{\mathrm{3}}{v}_{\mathrm{1}} }{{L}}\right)^{\mathrm{2}} \right]={u}^{\mathrm{2}} \\ $$$$\mathrm{5}{v}_{\mathrm{1}} ^{\mathrm{2}} −{uv}_{\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow{v}_{\mathrm{1}} =\frac{{u}}{\mathrm{5}} \\ $$$$\Rightarrow\omega_{\mathrm{1}} =\frac{\mathrm{3}{u}}{\mathrm{5}{L}} \\ $$$${at}\:{time}\:{t}\:{point}\:{A}\:{crosses}\:{the}\:{y}−{axis}: \\ $$$${x}_{{A}} =\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\left(\omega_{\mathrm{1}} {t}\right)=\mathrm{0} \\ $$$$\Rightarrow\omega_{\mathrm{1}} {t}=\frac{\mathrm{3}{ut}}{\mathrm{5}{L}}=\frac{\pi}{\mathrm{2}}\: \\ $$$$\Rightarrow{t}=\frac{\mathrm{5}\pi{L}}{\mathrm{6}{u}}\:\checkmark \\ $$$${y}_{{A}} ={v}_{\mathrm{1}} {t}+\frac{{L}}{\mathrm{2}}\:\mathrm{sin}\:\left(\omega_{\mathrm{1}} {t}\right)=\frac{{L}\omega_{\mathrm{1}} {t}}{\mathrm{3}}+\frac{{L}}{\mathrm{2}}\:\mathrm{sin}\:\left(\omega_{\mathrm{1}} {t}\right) \\ $$$$\:\:\:\:\:=\frac{{L}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}+\mathrm{1}\right)\:>{L} \\ $$$$================== \\ $$$$\theta_{\mathrm{1}} =\omega_{\mathrm{1}} {t}=\frac{\mathrm{3}{ut}}{\mathrm{5}{L}} \\ $$$${x}_{\mathrm{1}} =\mathrm{0} \\ $$$${y}_{\mathrm{1}} ={v}_{\mathrm{1}} {t}=\frac{{ut}}{\mathrm{5}} \\ $$$${x}_{{A}} ={x}_{\mathrm{1}} +\frac{{L}\:\mathrm{cos}\:\theta_{\mathrm{1}} }{\mathrm{2}}=\frac{{L}\:\mathrm{cos}\:\left(\frac{\mathrm{3}{ut}}{\mathrm{5}{L}}\right)}{\mathrm{2}} \\ $$$${y}_{{A}} ={y}_{\mathrm{1}} +\frac{{L}\:\mathrm{sin}\:\theta_{\mathrm{1}} }{\mathrm{2}}=\frac{{ut}}{\mathrm{5}}+\frac{{L}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{ut}}{\mathrm{5}{L}}\right)}{\mathrm{2}} \\ $$$$\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{6}}+\omega_{\mathrm{2}} {t}=\frac{\pi}{\mathrm{6}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}{ut}}{\mathrm{5}{L}} \\ $$$${x}_{\mathrm{2}} =\frac{{L}}{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}{L}}{\mathrm{4}}+{u}_{\mathrm{2}} {t}=\frac{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){L}}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}{ut}}{\mathrm{2}} \\ $$$${y}_{\mathrm{2}} =−\frac{{L}}{\mathrm{4}}+{v}_{\mathrm{2}} {t}=−\frac{{L}}{\mathrm{4}}+\frac{\mathrm{3}{ut}}{\mathrm{10}} \\ $$$${x}_{{D}} ={x}_{\mathrm{2}} +\frac{{L}\:\mathrm{cos}\:\theta_{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){L}}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}{ut}}{\mathrm{2}}+\frac{{L}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}{ut}}{\mathrm{5}{L}}\right)}{\mathrm{2}} \\ $$$${y}_{{D}} ={y}_{\mathrm{2}} +\frac{{L}\:\mathrm{sin}\:\theta_{\mathrm{2}} }{\mathrm{2}}=−\frac{{L}}{\mathrm{4}}+\frac{\mathrm{3}{ut}}{\mathrm{10}}+\frac{{L}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}{ut}}{\mathrm{5}{L}}\right)}{\mathrm{2}} \\ $$$$================== \\ $$$${following}\:{pictures}\:{are}\:{showing}\:{the} \\ $$$${movement}\:{of}\:{the}\:{rods}\:{after}\:{the} \\ $$$${collision}\:{as}\:{well}\:{as}\:{the}\:{locus}\:{of}\:{the} \\ $$$${points}\:{A}\:{and}\:{D}. \\ $$
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
Commented by mr W last updated on 02/Jan/25
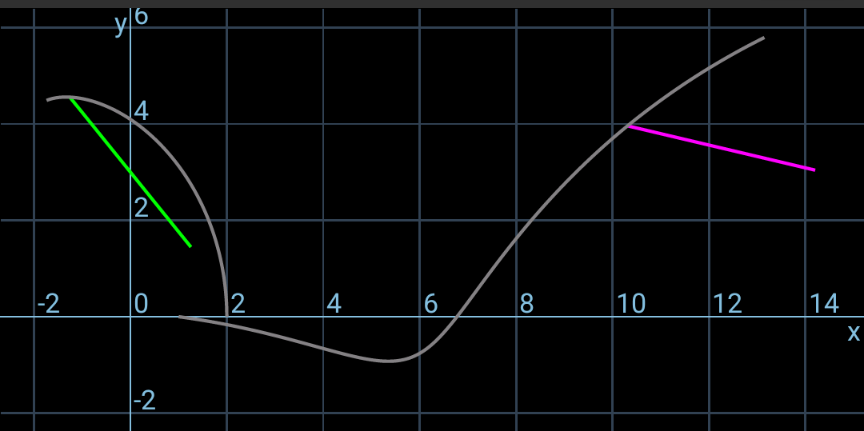
Commented by mr W last updated on 02/Jan/25
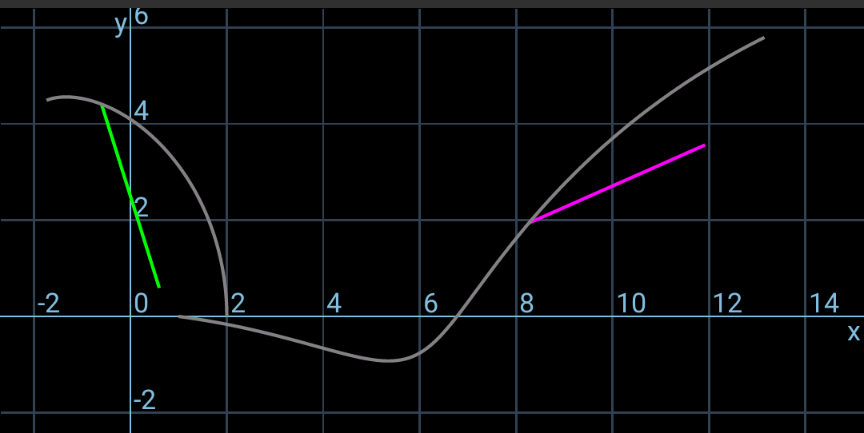
Commented by ajfour last updated on 02/Jan/25
$${beautiful}\:{omg}!\:{how}\:{you}\:{generate}\:{this}. \\ $$
Commented by mr W last updated on 02/Jan/25

$${i}\:{just}\:{have}\:{used}\:{the}\:{app}\:{Grapher} \\ $$$${like}\:{following}. \\ $$$$\left({with}\:{m}={ut}\:{in}\:{the}\:{equations}\right) \\ $$
Commented by mr W last updated on 02/Jan/25
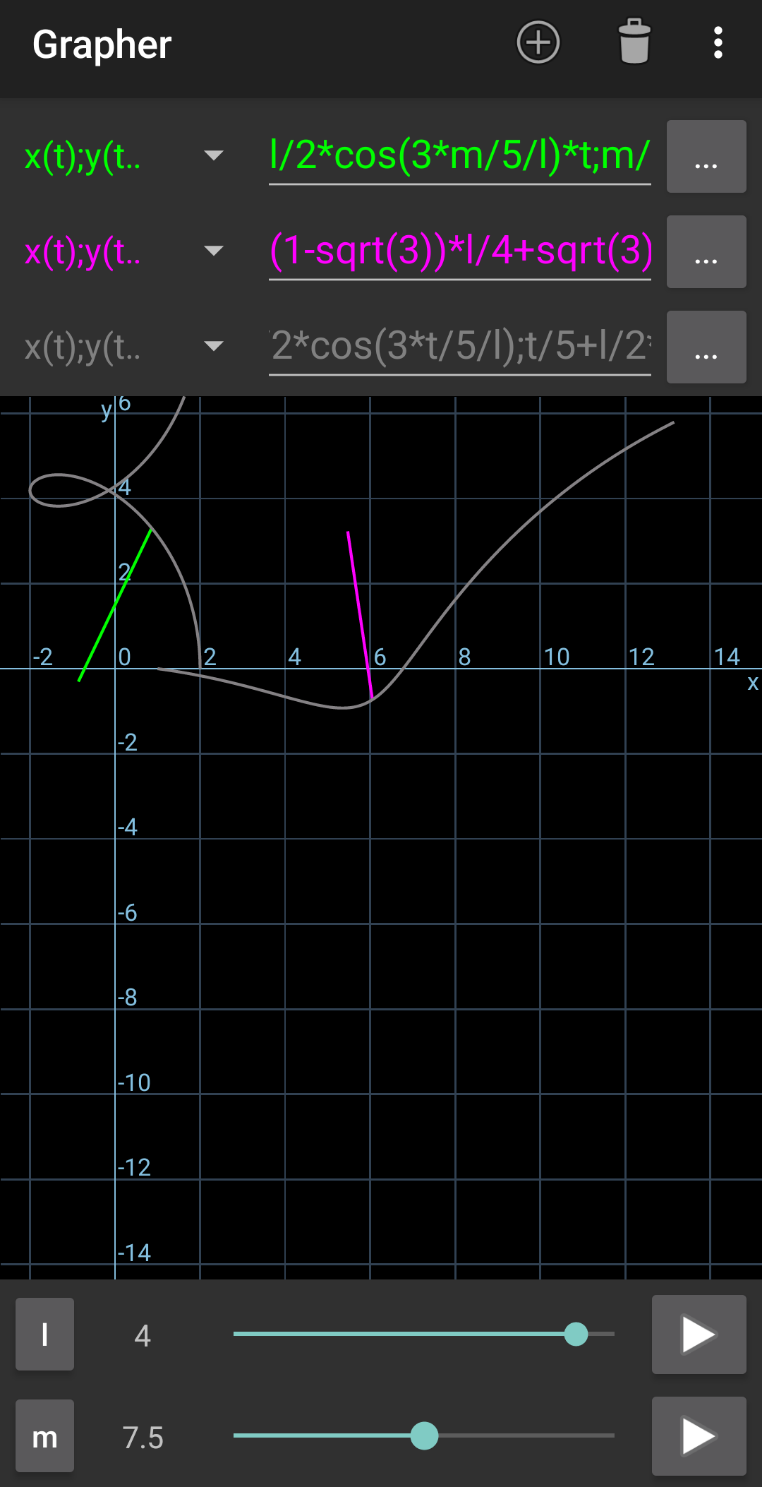
Commented by mr W last updated on 02/Jan/25

$${we}\:{can}\:{even}\:{generate}\:{an}\:{animation}. \\ $$$${but}\:{since}\:{this}\:{app}\:{doesn}'{t}\:{support}\: \\ $$$${animated}\:{gif}\:{images},\:{so}\:{i}\:{just}\:{took} \\ $$$${some}\:{screenshots}\:{for}\:{different} \\ $$$${values}\:{of}\:{m}. \\ $$
Commented by MathematicalUser2357 last updated on 17/Feb/25

$${So}\:{I}\:{have}\:{a}\:{Grapher}\:{Free}: \\ $$
