Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 215232 by Mingma last updated on 01/Jan/25

Answered by devdutt last updated on 01/Jan/25

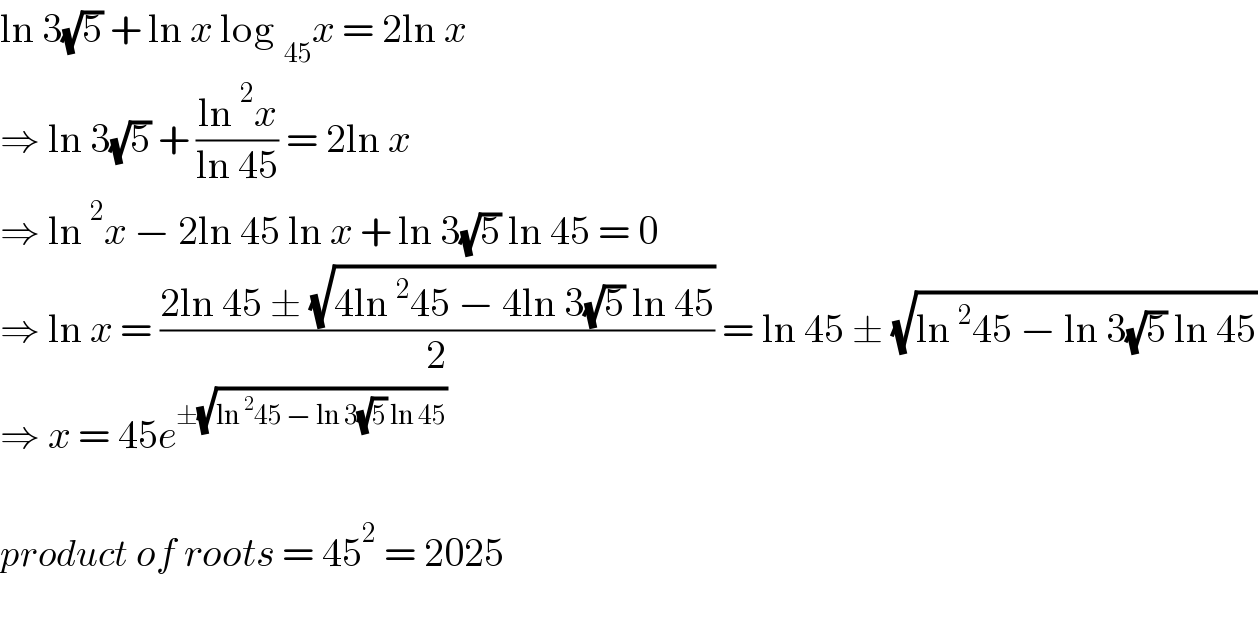
ln 3(√5) + ln x log _(45) x = 2ln x ⇒ ln 3(√5) + ((ln^2 x)/(ln 45)) = 2ln x ⇒ ln^2 x − 2ln 45 ln x + ln 3(√5) ln 45 = 0 ⇒ ln x = ((2ln 45 ± (√(4ln^2 45 − 4ln 3(√5) ln 45)))/2) = ln 45 ± (√(ln^2 45 − ln 3(√5) ln 45)) ⇒ x = 45e^(±(√(ln^2 45 − ln 3(√5) ln 45))) product of roots = 45^2 = 2025

$$\mathrm{ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:+\:\mathrm{ln}\:{x}\:\mathrm{log}\:_{\mathrm{45}} {x}\:=\:\mathrm{2ln}\:{x}\: \\ $$$$\Rightarrow\:\mathrm{ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:+\:\frac{\mathrm{ln}\:^{\mathrm{2}} {x}}{\mathrm{ln}\:\mathrm{45}}\:=\:\mathrm{2ln}\:{x}\: \\ $$$$\Rightarrow\:\mathrm{ln}\:^{\mathrm{2}} {x}\:−\:\mathrm{2ln}\:\mathrm{45}\:\mathrm{ln}\:{x}\:+\:\mathrm{ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:\mathrm{ln}\:\mathrm{45}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{ln}\:{x}\:=\:\frac{\mathrm{2ln}\:\mathrm{45}\:\pm\:\sqrt{\mathrm{4ln}\:^{\mathrm{2}} \mathrm{45}\:−\:\mathrm{4ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:\mathrm{ln}\:\mathrm{45}}}{\mathrm{2}}\:=\:\mathrm{ln}\:\mathrm{45}\:\pm\:\sqrt{\mathrm{ln}\:^{\mathrm{2}} \mathrm{45}\:−\:\mathrm{ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:\mathrm{ln}\:\mathrm{45}} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{45}{e}^{\pm\sqrt{\mathrm{ln}\:^{\mathrm{2}} \mathrm{45}\:−\:\mathrm{ln}\:\mathrm{3}\sqrt{\mathrm{5}}\:\mathrm{ln}\:\mathrm{45}}} \\ $$$$ \\ $$$${product}\:{of}\:{roots}\:=\:\mathrm{45}^{\mathrm{2}} \:=\:\mathrm{2025} \\ $$$$ \\ $$

Commented by Mingma last updated on 02/Jan/25

Perfect ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com