Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 215230 by Mingma last updated on 01/Jan/25

Answered by A5T last updated on 01/Jan/25

Commented by A5T last updated on 01/Jan/25

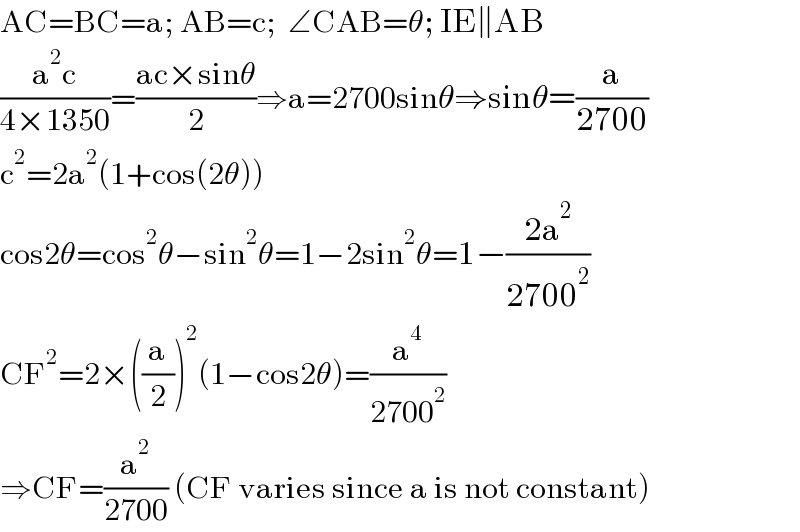
AC=BC=a; AB=c; ∠CAB=θ; IE∥AB ((a^2 c)/(4×1350))=((ac×sinθ)/2)⇒a=2700sinθ⇒sinθ=(a/(2700)) c^2 =2a^2 (1+cos(2θ)) cos2θ=cos^2 θ−sin^2 θ=1−2sin^2 θ=1−((2a^2 )/(2700^2 )) CF^2 =2×((a/2))^2 (1−cos2θ)=(a^4 /(2700^2 )) ⇒CF=(a^2 /(2700)) (CF varies since a is not constant)

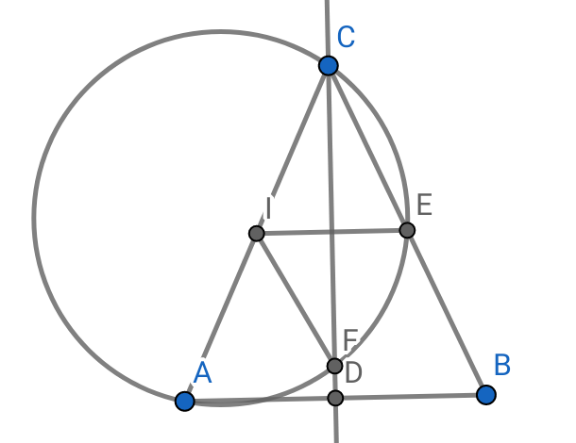
$$\mathrm{AC}=\mathrm{BC}=\mathrm{a};\:\mathrm{AB}=\mathrm{c};\:\:\angle\mathrm{CAB}=\theta;\:\mathrm{IE}\parallel\mathrm{AB} \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} \mathrm{c}}{\mathrm{4}×\mathrm{1350}}=\frac{\mathrm{ac}×\mathrm{sin}\theta}{\mathrm{2}}\Rightarrow\mathrm{a}=\mathrm{2700sin}\theta\Rightarrow\mathrm{sin}\theta=\frac{\mathrm{a}}{\mathrm{2700}} \\ $$$$\mathrm{c}^{\mathrm{2}} =\mathrm{2a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right) \\ $$$$\mathrm{cos2}\theta=\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \theta=\mathrm{1}−\frac{\mathrm{2a}^{\mathrm{2}} }{\mathrm{2700}^{\mathrm{2}} } \\ $$$$\mathrm{CF}^{\mathrm{2}} =\mathrm{2}×\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos2}\theta\right)=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{2700}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{CF}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2700}}\:\left(\mathrm{CF}\:\mathrm{varies}\:\mathrm{since}\:\mathrm{a}\:\mathrm{is}\:\mathrm{not}\:\mathrm{constant}\right) \\ $$

Commented by Mingma last updated on 02/Jan/25

Perfect ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com