
Question Number 215229 by Mingma last updated on 01/Jan/25
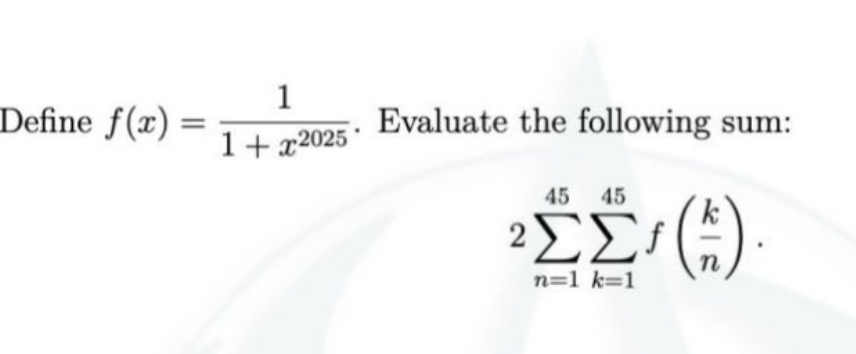
Answered by devdutt last updated on 01/Jan/25
![1. f((k/n)) = (n^(2025) /(n^(2025) +k^(2025) )) 2. f((k/n))+f((n/k)) = 1, f((n/n)) = f(1)= (1/2) 3. {(k/n)}_(k,n∈[45]) ⊃ {(k/n),(n/k)}, ∀k,n∈[45] 4. 2Σ_(n∈[45]) Σ_(k∈[45]) f((k/n)) = 2Σ_(n∈[45]) f((n/n)) + 2Σ_(n∈[45]) Σ_(k∈[45]−{n}) ((f(k/n)+f(n/k))/2) = 2×((45)/2) + 2×((45×44)/2) = 45^2 = 2025](Q215239.png)
$$\mathrm{1}.\:{f}\left(\frac{{k}}{{n}}\right)\:=\:\frac{{n}^{\mathrm{2025}} }{{n}^{\mathrm{2025}} +{k}^{\mathrm{2025}} } \\ $$$$ \\ $$$$\mathrm{2}.\:{f}\left(\frac{{k}}{{n}}\right)+{f}\left(\frac{{n}}{{k}}\right)\:=\:\mathrm{1},\: \\ $$$$\:\:\:\:{f}\left(\frac{{n}}{{n}}\right)\:=\:{f}\left(\mathrm{1}\right)=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{3}.\:\left\{\frac{{k}}{{n}}\right\}_{{k},{n}\in\left[\mathrm{45}\right]} \supset\:\left\{\frac{{k}}{{n}},\frac{{n}}{{k}}\right\},\:\forall{k},{n}\in\left[\mathrm{45}\right] \\ $$$$ \\ $$$$\mathrm{4}.\:\mathrm{2}\underset{{n}\in\left[\mathrm{45}\right]} {\sum}\underset{{k}\in\left[\mathrm{45}\right]} {\sum}{f}\left(\frac{{k}}{{n}}\right)\:=\:\mathrm{2}\underset{{n}\in\left[\mathrm{45}\right]} {\sum}{f}\left(\frac{{n}}{{n}}\right)\:+\:\mathrm{2}\underset{{n}\in\left[\mathrm{45}\right]} {\sum}\underset{{k}\in\left[\mathrm{45}\right]−\left\{{n}\right\}} {\sum}\frac{{f}\left({k}/{n}\right)+{f}\left({n}/{k}\right)}{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{2}×\frac{\mathrm{45}}{\mathrm{2}}\:+\:\mathrm{2}×\frac{\mathrm{45}×\mathrm{44}}{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{45}^{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{2025} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by Mingma last updated on 01/Jan/25
Perfect ��
