
Question Number 215193 by MATHEMATICSAM last updated on 31/Dec/24

Commented by MATHEMATICSAM last updated on 31/Dec/24
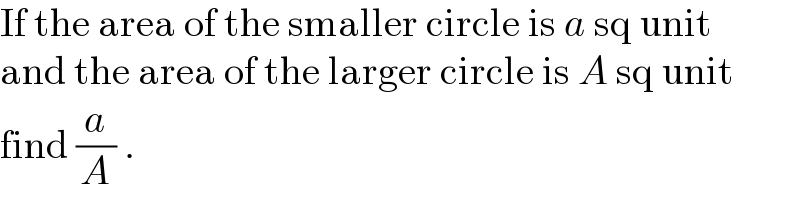
$$\mathrm{If}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{circle}\:\mathrm{is}\:{a}\:\mathrm{sq}\:\mathrm{unit} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{larger}\:\mathrm{circle}\:\mathrm{is}\:{A}\:\mathrm{sq}\:\mathrm{unit} \\ $$$$\mathrm{find}\:\frac{{a}}{{A}}\:. \\ $$
Answered by som(math1967) last updated on 31/Dec/24
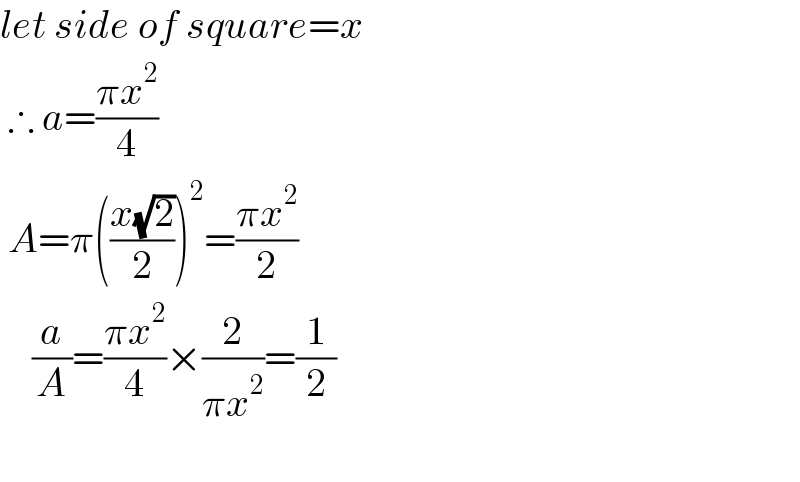
$${let}\:{side}\:{of}\:{square}={x} \\ $$$$\:\therefore\:{a}=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:{A}=\pi\left(\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\frac{{a}}{{A}}=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{4}}×\frac{\mathrm{2}}{\pi{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by mr W last updated on 02/Jan/25
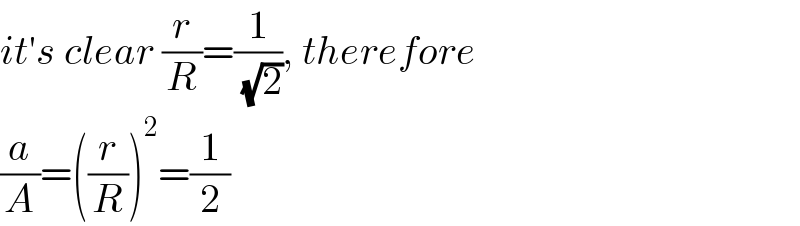
$${it}'{s}\:{clear}\:\frac{{r}}{{R}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}},\:{therefore}\: \\ $$$$\frac{{a}}{{A}}=\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$
