
Question Number 214815 by mr W last updated on 20/Dec/24
Commented by mr W last updated on 20/Dec/24

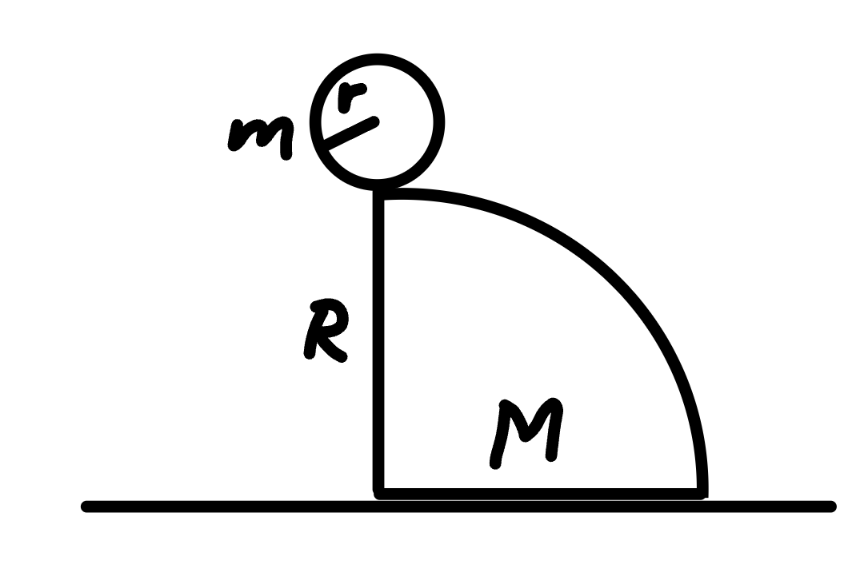
$${a}\:{solid}\:{ball}\:{with}\:{mass}\:\boldsymbol{{m}}\:{and}\:{radius}\:\boldsymbol{{r}} \\ $$$${is}\:{released}\:{from}\:{the}\:{top}\:{of}\:{a} \\ $$$${quarter}−{cylindrical}\:{wedge}\:{with} \\ $$$${mass}\:\boldsymbol{{M}}\:{and}\:{radius}\:\boldsymbol{{R}}\:{as}\:{shown}. \\ $$$${there}\:{is}\:{enough}\:{friction}\:{between} \\ $$$${ball}\:{and}\:{wedge},\:{but}\:{there}\:{is}\:{no} \\ $$$${friction}\:{between}\:{wedge}\:{and}\:{ground}. \\ $$$${find}\:{the}\:{final}\:{speed}\:{of}\:{the}\:{wedge}. \\ $$
Answered by aleks041103 last updated on 21/Dec/24

Commented by aleks041103 last updated on 21/Dec/24

Commented by mr W last updated on 21/Dec/24
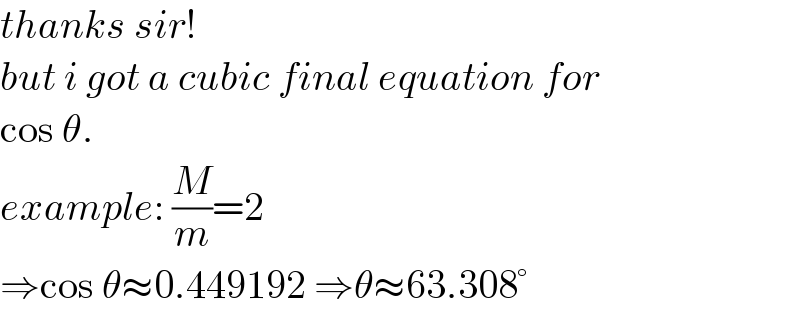
$${thanks}\:{sir}!\: \\ $$$${but}\:{i}\:{got}\:{a}\:{cubic}\:{final}\:{equation}\:{for} \\ $$$$\mathrm{cos}\:\theta. \\ $$$${example}:\:\frac{{M}}{{m}}=\mathrm{2}\: \\ $$$$\Rightarrow\mathrm{cos}\:\theta\approx\mathrm{0}.\mathrm{449192}\:\Rightarrow\theta\approx\mathrm{63}.\mathrm{308}° \\ $$
Answered by mr W last updated on 21/Dec/24
Commented by mr W last updated on 21/Dec/24
![center of quarter circle (X, 0) center of ball (x, y) let k=(M/m)+1 x=X+(R+r)sin θ y=(R+r)cos θ rotation of ball: ϕ=(1+(R/r))θ (dϕ/dt)=(1+(R/r))(dθ/dt)=(1+(R/r))ω α=(d^2 ϕ/dt^2 )=(1+(R/r))ω(dω/dθ) U=−(dX/dt) (←) u=(dx/dt)=−U+(R+r)ω cos θ (→) v=−(dy/dt)=(R+r)ω sin θ (↓) MU=mu=−mU+m(R+r)ω cos θ ⇒U=(((R+r)ω cos θ)/k) mg(R+r)(1−cos θ)=((MU^2 )/2)+((m(u^2 +v^2 ))/2)+(I/2)((dϕ/dt))^2 2g(R+r)(1−cos θ)=((M/m)+1)U^2 +(R+r)^2 ω^2 −2U(R+r)ω cos θ+((2(R+r)^2 ω^2 )/5) 2g(R+r)(1−cos θ)=((M/m)+1)U^2 +((7(R+r)^2 ω^2 )/5)−2U(R+r)ω cos θ 2g(1−cos θ)=(R+r)ω^2 ((7/5)−((cos^2 θ)/((M/m)+1))) ⇒ω^2 =((2kg(1−cos θ))/((R+r)(((7k)/5)−cos^2 θ))) ω(dω/dθ)=((kg sin θ (cos^2 θ−2 cos θ+((7k)/5)))/((R+r)(((7k)/5)−cos^2 θ)^2 )) −fr=Iα −fr=((2mr^2 )/5)×(1+(R/r))ω(dω/dθ) f=−((2m(R+r))/5)×((kg sin θ (cos^2 θ−2 cos θ+((7k)/5)))/((R+r)(((7k)/5)−cos^2 θ)^2 )) f=−((2kmg sin θ (cos^2 θ−2 cos θ+((7k)/5)))/(5(((7k)/5)−cos^2 θ)^2 )) A=(dU/dt)=(((R+r)ω)/k)[−ω sin θ+cos θ (dω/dθ)] A=((g sin θ(−cos^3 θ+((21k)/5) cos θ−((14k)/5)))/((((7k)/5)−cos^2 θ)^2 )) N sin θ+f cos θ=MA N sinθ−((2kmg sin θ (cos^2 θ−2 cos θ+((7k)/5))cos θ)/(5(((7k)/5)−cos^2 θ)^2 ))=((Mg sin θ(−cos^3 θ+((21k)/5) cos θ−((14k)/5)))/((((7k)/5)−cos^2 θ)^2 )) N=0: 2k(cos^2 θ−2 cos θ+((7k)/5))cos θ+5(k−1)(−cos^3 θ+((21k)/5) cos θ−((14k)/5)) 5(−3k+5)cos^3 θ−20k cos^2 θ+(119k^2 −105) cos θ−70k(k−1)=0 (r/(R+r))≤cos θ<1 (U/( (√(g(R+r)))))=cos θ(√((2(1−cos θ))/(k(((7k)/5)−cos^2 θ))))](Q214842.png)
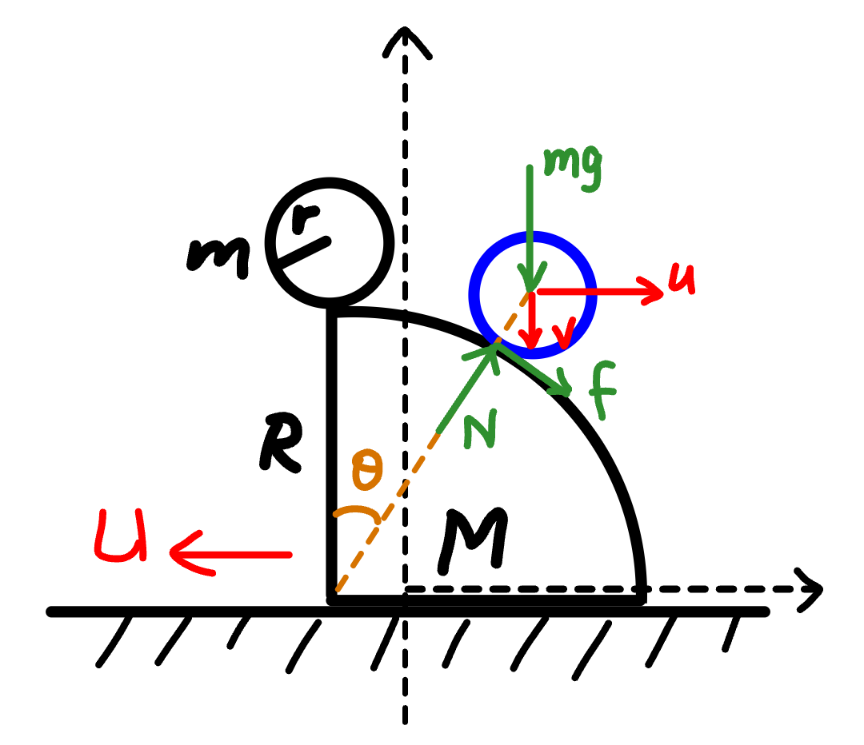
$${center}\:{of}\:{quarter}\:{circle}\:\left({X},\:\mathrm{0}\right) \\ $$$${center}\:{of}\:{ball}\:\left({x},\:{y}\right) \\ $$$${let}\:{k}=\frac{{M}}{{m}}+\mathrm{1} \\ $$$${x}={X}+\left({R}+{r}\right)\mathrm{sin}\:\theta \\ $$$${y}=\left({R}+{r}\right)\mathrm{cos}\:\theta \\ $$$${rotation}\:{of}\:{ball}: \\ $$$$\varphi=\left(\mathrm{1}+\frac{{R}}{{r}}\right)\theta \\ $$$$\frac{{d}\varphi}{{dt}}=\left(\mathrm{1}+\frac{{R}}{{r}}\right)\frac{{d}\theta}{{dt}}=\left(\mathrm{1}+\frac{{R}}{{r}}\right)\omega \\ $$$$\alpha=\frac{{d}^{\mathrm{2}} \varphi}{{dt}^{\mathrm{2}} }=\left(\mathrm{1}+\frac{{R}}{{r}}\right)\omega\frac{{d}\omega}{{d}\theta} \\ $$$${U}=−\frac{{dX}}{{dt}}\:\:\:\:\:\left(\leftarrow\right) \\ $$$${u}=\frac{{dx}}{{dt}}=−{U}+\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta\:\:\:\:\:\left(\rightarrow\right) \\ $$$${v}=−\frac{{dy}}{{dt}}=\left({R}+{r}\right)\omega\:\mathrm{sin}\:\theta\:\:\:\:\:\left(\downarrow\right) \\ $$$${MU}={mu}=−{mU}+{m}\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{U}=\frac{\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta}{{k}} \\ $$$${mg}\left({R}+{r}\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\frac{{MU}^{\mathrm{2}} }{\mathrm{2}}+\frac{{m}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)}{\mathrm{2}}+\frac{{I}}{\mathrm{2}}\left(\frac{{d}\varphi}{{dt}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{g}\left({R}+{r}\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\left(\frac{{M}}{{m}}+\mathrm{1}\right){U}^{\mathrm{2}} +\left({R}+{r}\right)^{\mathrm{2}} \omega^{\mathrm{2}} −\mathrm{2}{U}\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta+\frac{\mathrm{2}\left({R}+{r}\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\mathrm{2}{g}\left({R}+{r}\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\left(\frac{{M}}{{m}}+\mathrm{1}\right){U}^{\mathrm{2}} +\frac{\mathrm{7}\left({R}+{r}\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{5}}−\mathrm{2}{U}\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta \\ $$$$\mathrm{2}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\left({R}+{r}\right)\omega^{\mathrm{2}} \left(\frac{\mathrm{7}}{\mathrm{5}}−\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\frac{{M}}{{m}}+\mathrm{1}}\right) \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{2}{kg}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{\left({R}+{r}\right)\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)} \\ $$$$\omega\frac{{d}\omega}{{d}\theta}=\frac{{kg}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{7}{k}}{\mathrm{5}}\right)}{\left({R}+{r}\right)\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$$−{fr}={I}\alpha \\ $$$$−{fr}=\frac{\mathrm{2}{mr}^{\mathrm{2}} }{\mathrm{5}}×\left(\mathrm{1}+\frac{{R}}{{r}}\right)\omega\frac{{d}\omega}{{d}\theta} \\ $$$${f}=−\frac{\mathrm{2}{m}\left({R}+{r}\right)}{\mathrm{5}}×\frac{{kg}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{7}{k}}{\mathrm{5}}\right)}{\left({R}+{r}\right)\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${f}=−\frac{\mathrm{2}{kmg}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{7}{k}}{\mathrm{5}}\right)}{\mathrm{5}\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}=\frac{{dU}}{{dt}}=\frac{\left({R}+{r}\right)\omega}{{k}}\left[−\omega\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\frac{{d}\omega}{{d}\theta}\right] \\ $$$${A}=\frac{{g}\:\mathrm{sin}\:\theta\left(−\mathrm{cos}^{\mathrm{3}} \:\theta+\frac{\mathrm{21}{k}}{\mathrm{5}}\:\mathrm{cos}\:\theta−\frac{\mathrm{14}{k}}{\mathrm{5}}\right)}{\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${N}\:\mathrm{sin}\:\theta+{f}\:\mathrm{cos}\:\theta={MA} \\ $$$${N}\:\mathrm{sin}\theta−\frac{\mathrm{2}{kmg}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{7}{k}}{\mathrm{5}}\right)\mathrm{cos}\:\theta}{\mathrm{5}\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }=\frac{{Mg}\:\mathrm{sin}\:\theta\left(−\mathrm{cos}^{\mathrm{3}} \:\theta+\frac{\mathrm{21}{k}}{\mathrm{5}}\:\mathrm{cos}\:\theta−\frac{\mathrm{14}{k}}{\mathrm{5}}\right)}{\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${N}=\mathrm{0}: \\ $$$$\mathrm{2}{k}\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{7}{k}}{\mathrm{5}}\right)\mathrm{cos}\:\theta+\mathrm{5}\left({k}−\mathrm{1}\right)\left(−\mathrm{cos}^{\mathrm{3}} \:\theta+\frac{\mathrm{21}{k}}{\mathrm{5}}\:\mathrm{cos}\:\theta−\frac{\mathrm{14}{k}}{\mathrm{5}}\right) \\ $$$$\mathrm{5}\left(−\mathrm{3}{k}+\mathrm{5}\right)\mathrm{cos}^{\mathrm{3}} \:\theta−\mathrm{20}{k}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\left(\mathrm{119}{k}^{\mathrm{2}} −\mathrm{105}\right)\:\mathrm{cos}\:\theta−\mathrm{70}{k}\left({k}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{{r}}{{R}+{r}}\leqslant\mathrm{cos}\:\theta<\mathrm{1} \\ $$$$\frac{{U}}{\:\sqrt{{g}\left({R}+{r}\right)}}=\mathrm{cos}\:\theta\sqrt{\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{{k}\left(\frac{\mathrm{7}{k}}{\mathrm{5}}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)}} \\ $$
Commented by aleks041103 last updated on 21/Dec/24

$${In}\:{your}\:{energy}\:{conservation}\:{eqn}\:{you}\:{missed} \\ $$$${to}\:{account}\:{for}\:{the}\:{rotational}\:{kinetic}\:{energy}. \\ $$
Commented by mr W last updated on 22/Dec/24

$${you}'{re}\:{right}.\:{now}\:{it}'{s}\:{fixed}. \\ $$
Commented by ajfour last updated on 21/Dec/24
Awesome Watch this another geometry video i made. https://youtu.be/JOiE3jnIDvs?si=ADUmXZ0DRrw7MxD_
Commented by mr W last updated on 21/Dec/24
��
