Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 214793 by vijaysahu last updated on 19/Dec/24

Commented by Tinku Tara last updated on 20/Dec/24

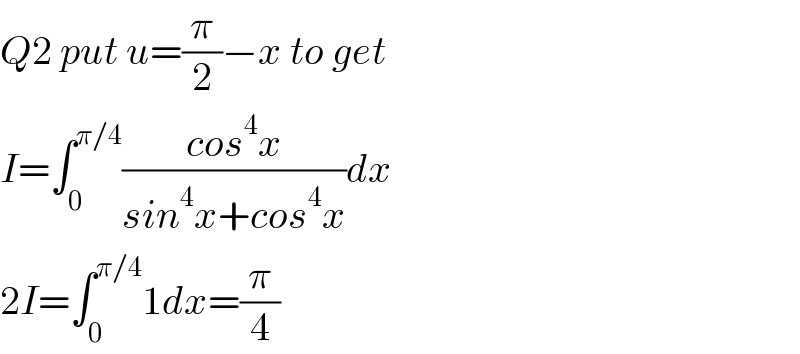
Q2 put u=(π/2)−x to get I=∫_0 ^(π/4) ((cos^4 x)/(sin^4 x+cos^4 x))dx 2I=∫_0 ^(π/4) 1dx=(π/4)

$${Q}\mathrm{2}\:{put}\:{u}=\frac{\pi}{\mathrm{2}}−{x}\:{to}\:{get} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{cos}^{\mathrm{4}} {x}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{1}{dx}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by Tinku Tara last updated on 20/Dec/24

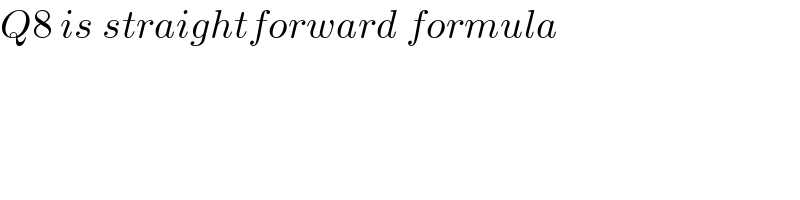
Q8 is straightforward formula

$${Q}\mathrm{8}\:{is}\:{straightforward}\:{formula} \\ $$

Answered by MathematicalUser2357 last updated on 20/Dec/24

Q1 ∫(1/( (√(tan x))+1))dx=∫sec^2 x∙(1/(((√(tan x))+1)(tan^2 x+1)))dx ⇒^(u=tan x⇒du=sec^2 xdx) ∫(1/(((√u)+1)(u^2 +1)))du ⇒^(v=(√u)⇒du=(1/(2(√u)))du) 2∫(v/((v+1)(v^4 +1)))dv Now we′re integrating the red side ∫(v/((v+1)(v^4 +1)))dv=∫(((v^3 −v^2 +v+1)/(2(v^4 +1)))−(1/(2(v+1))))dv =(1/2)∫((v^3 −v^2 +v+1)/(v^4 +1))dv−(1/2)∫(1/(v+1))dv Now we′re integrating the blue side ∫((v^3 −v^2 +v+1)/(v^4 +1))dv=∫((v^3 −v^2 +v+1)/((v^2 −(√2)v+1)(u^2 +(√2)v+1)))dv =∫(((((√2)+2)v+(√2))/(2^(3/2) (v^2 +(√2)v+1)))+((((√2)−2)v+(√2))/(2^(3/2) (v^2 −(√2)+1))))dv =(1/2^(3/2) )∫((((√2)+2)v+(√2))/(v^2 +(√2)v+1))dv+(1/2^(3/2) )∫((((√2)−2)v+(√2))/(v^2 −(√2)v+1))dv Now we′re integrating the brown side ∫((((√2)+2)v+(√2))/(v^2 +(√2)v+1))dv=∫(((((√2)+2)(2v+(√2)))/(2(v^2 +(√2)v+1)))+(((√2)−(((√2)+2)/( (√2))))/(v^2 +(√2)v+1)))dv =(((√2)+2)/2)∫((2v+(√2))/(v^2 +(√2)v+1))dv+((√2)−(((√2)+2)/( (√2))))∫(1/(v^2 +(√2)v+1))dv Holy...god...what a long integral expression Now we′re integrating the black side#2 ∫((2v+(√2))/(v^2 +(√2)v+1))dv⇒^(w=v^2 +(√2)v+1⇒dv=(2v+(√2))dv) ∫(1/w)dw=ln w=ln(v^2 +(√2)v+1) ∫(1/(v^2 +(√2)v+1))dv=∫(1/((v+(1/( (√2))))^2 +(1/2)))dv ⇒^(w=(√2)v+1⇒dw=(√2)dv) ∫(1/( (√2)((w^2 /2)+(1/2))))dw=(1/( (√2)))∫(1/(w^2 +1))dw=(1/( (√2)))tan^(−1) w =(1/( (√2)))tan^(−1) ((√2)v+1) =(((√2)+2)/2)∫((2v+(√2))/(v^2 +(√2)v+1))dv+((√2)−(((√2)+2)/( (√2))))∫(1/(v^2 +(√2)v+1))dv =((((√2)+2)ln(v^2 +(√2)v+1))/2)+(√2)((√2)−(((√2)+2)/( (√2))))tan^(−1) ((√2)v+1) ... ...=Holy...god...what a terrible integral question

$${Q}\mathrm{1}\:\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{x}}+\mathrm{1}}{dx}=\int\mathrm{sec}^{\mathrm{2}} {x}\centerdot\frac{\mathrm{1}}{\left(\sqrt{\mathrm{tan}\:{x}}+\mathrm{1}\right)\left(\mathrm{tan}^{\mathrm{2}} {x}+\mathrm{1}\right)}{dx} \\ $$$$\overset{{u}=\mathrm{tan}\:{x}\Rightarrow{du}=\mathrm{sec}^{\mathrm{2}} {xdx}} {\Rightarrow}\int\frac{\mathrm{1}}{\left(\sqrt{{u}}+\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{du} \\ $$$$\overset{{v}=\sqrt{{u}}\Rightarrow{du}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}}{du}} {\Rightarrow}\mathrm{2}\int\frac{{v}}{\left({v}+\mathrm{1}\right)\left({v}^{\mathrm{4}} +\mathrm{1}\right)}{dv} \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}'\boldsymbol{\mathrm{re}}\:\boldsymbol{\mathrm{integrating}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{red}}\:\boldsymbol{\mathrm{side}} \\ $$$$\int\frac{{v}}{\left({v}+\mathrm{1}\right)\left({v}^{\mathrm{4}} +\mathrm{1}\right)}{dv}=\int\left(\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +{v}+\mathrm{1}}{\mathrm{2}\left({v}^{\mathrm{4}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({v}+\mathrm{1}\right)}\right){dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +{v}+\mathrm{1}}{{v}^{\mathrm{4}} +\mathrm{1}}{dv}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{v}+\mathrm{1}}{dv} \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}'\boldsymbol{\mathrm{re}}\:\boldsymbol{\mathrm{integrating}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{blue}}\:\boldsymbol{\mathrm{side}} \\ $$$$\int\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +{v}+\mathrm{1}}{{v}^{\mathrm{4}} +\mathrm{1}}{dv}=\int\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} +{v}+\mathrm{1}}{\left({v}^{\mathrm{2}} −\sqrt{\mathrm{2}}{v}+\mathrm{1}\right)\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\right)}{dv} \\ $$$$=\int\left(\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right){v}+\sqrt{\mathrm{2}}}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\right)}+\frac{\left(\sqrt{\mathrm{2}}−\mathrm{2}\right){v}+\sqrt{\mathrm{2}}}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({v}^{\mathrm{2}} −\sqrt{\mathrm{2}}+\mathrm{1}\right)}\right){dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} }\int\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right){v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}+\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} }\int\frac{\left(\sqrt{\mathrm{2}}−\mathrm{2}\right){v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} −\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv} \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}'\boldsymbol{\mathrm{re}}\:\boldsymbol{\mathrm{integrating}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{brown}}\:\boldsymbol{\mathrm{side}} \\ $$$$\int\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right){v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}=\int\left(\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)\left(\mathrm{2}{v}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}\left({v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\right)}+\frac{\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}\right){dv} \\ $$$$=\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{2}}\int\frac{\mathrm{2}{v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}+\left(\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)\int\frac{\mathrm{1}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv} \\ $$$$\mathcal{H}\mathrm{oly}...\mathrm{god}...\mathrm{what}\:\mathrm{a}\:\mathrm{long}\:\mathrm{integral}\:\mathrm{expression} \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}'\boldsymbol{\mathrm{re}}\:\boldsymbol{\mathrm{integrating}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{black}}\:\boldsymbol{\mathrm{side}}#\mathrm{2} \\ $$$$\int\frac{\mathrm{2}{v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}\overset{{w}={v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\Rightarrow{dv}=\left(\mathrm{2}{v}+\sqrt{\mathrm{2}}\right){dv}} {\Rightarrow}\int\frac{\mathrm{1}}{{w}}{dw}=\mathrm{ln}\:{w}=\mathrm{ln}\left({v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{1}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}=\int\frac{\mathrm{1}}{\left({v}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}{dv} \\ $$$$\overset{{w}=\sqrt{\mathrm{2}}{v}+\mathrm{1}\Rightarrow{dw}=\sqrt{\mathrm{2}}{dv}} {\Rightarrow}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\frac{{w}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dw}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}}{{w}^{\mathrm{2}} +\mathrm{1}}{dw}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} {w} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{v}+\mathrm{1}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{2}}\int\frac{\mathrm{2}{v}+\sqrt{\mathrm{2}}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv}+\left(\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)\int\frac{\mathrm{1}}{{v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}}{dv} \\ $$$$=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)\mathrm{ln}\left({v}^{\mathrm{2}} +\sqrt{\mathrm{2}}{v}+\mathrm{1}\right)}{\mathrm{2}}+\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{v}+\mathrm{1}\right) \\ $$$$...\:...=\mathcal{H}\mathrm{oly}...\mathrm{god}...\mathrm{what}\:\mathrm{a}\:\mathrm{terrible}\:\mathrm{integral}\:\mathrm{question} \\ $$

Commented by Tinku Tara last updated on 20/Dec/24

I=∫_(π/6) ^(π/3) (1/(1+(√(tanx))))dx ....(1) substitute u=(π/2)−x du=−dx x=(π/6)⇒u=(π/3) x=(π/3)⇒u=(π/2) I=∫_(π/3) ^(π/6) −(1/(1+(√(cotu))))du =∫_(π/6) ^(π/3) (1/(1+(√(cotu))))du=∫_(π/6) ^(π/3) ((√(tanu))/(1+(√(tanu))))du =∫_(π/6) ^(π/3) ((√(tanx))/(1+(√(tanx))))dx ...(2) add (1) and (2) 2I=∫_(π/6) ^(π/3) 1dx=(π/6)⇒I=(π/(12))

$${I}=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{1}+\sqrt{{tanx}}}{dx}\:\:\:\:....\left(\mathrm{1}\right) \\ $$$$\mathrm{substitute}\:{u}=\frac{\pi}{\mathrm{2}}−{x}\: \\ $$$${du}=−{dx} \\ $$$${x}=\frac{\pi}{\mathrm{6}}\Rightarrow{u}=\frac{\pi}{\mathrm{3}} \\ $$$${x}=\frac{\pi}{\mathrm{3}}\Rightarrow{u}=\frac{\pi}{\mathrm{2}} \\ $$$${I}=\int_{\pi/\mathrm{3}} ^{\pi/\mathrm{6}} −\frac{\mathrm{1}}{\mathrm{1}+\sqrt{{cotu}}}{du} \\ $$$$=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{1}+\sqrt{{cotu}}}{du}=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{\sqrt{{tanu}}}{\mathrm{1}+\sqrt{{tanu}}}{du} \\ $$$$=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{\sqrt{{tanx}}}{\mathrm{1}+\sqrt{{tanx}}}{dx}\:\:\:\:\:\:...\left(\mathrm{2}\right) \\ $$$${add}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{I}=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \mathrm{1}{dx}=\frac{\pi}{\mathrm{6}}\Rightarrow{I}=\frac{\pi}{\mathrm{12}} \\ $$

Commented by MathematicalUser2357 last updated on 26/Dec/24

Thanks��Equation editor owner

Answered by Simurdiera last updated on 20/Dec/24

Q.6 Area = πa^2

$${Q}.\mathrm{6}\:\:\:\:\:{Area}\:=\:\pi\mathrm{a}^{\mathrm{2}} \\ $$

Answered by Tinku Tara last updated on 20/Dec/24

Q4 put tan^(−1) x=u

$${Q}\mathrm{4} \\ $$$${put}\:{tan}^{−\mathrm{1}} {x}={u}\: \\ $$

Answered by TonyCWX08 last updated on 21/Dec/24

Q7. Area=πab

$${Q}\mathrm{7}. \\ $$$${Area}=\pi{ab} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com