
Question Number 214722 by mr W last updated on 18/Dec/24
Commented by mr W last updated on 18/Dec/24

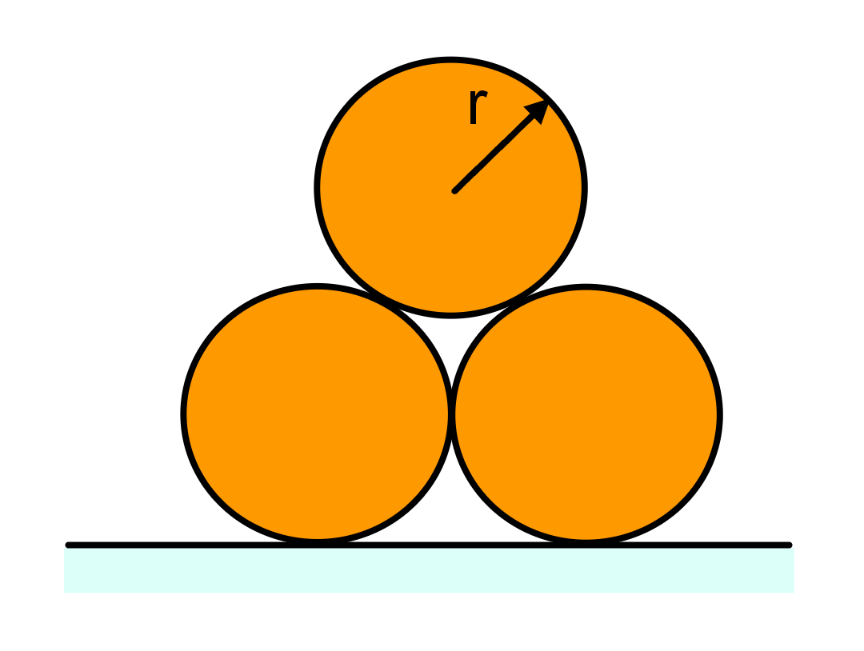
$${three}\:{identical}\:{cylinders}\:{are}\: \\ $$$${released}\:{from}\:{the}\:{state}\:{as}\:{shown}. \\ $$$${there}\:{is}\:{no}\:{friction}\:{anywhere}. \\ $$$${find}\: \\ $$$$\left.\mathrm{1}\right)\:{the}\:{final}\:{speed}\:{of}\:{the}\:{lower} \\ $$$${cylinders} \\ $$$$\left.\mathrm{2}\right)\:{after}\:{what}\:{time}\:{and}\:{with}\:{what} \\ $$$${speed}\:{the}\:{middle}\:{cylinder}\:{hits}\:{the} \\ $$$${ground} \\ $$
Answered by mr W last updated on 19/Dec/24
Commented by mr W last updated on 20/Dec/24
![m=mass of each cylinder ω=(dθ/dt) X=2r sin θ Y=2r cos θ U=(dX/dt)=2rω cos θ V=−(dY/dt)=2rω sin θ 2mgr(cos (π/6)−cos θ)=2×((mU^2 )/2)+((mV^2 )/2) 4gr(((√3)/2)−cos θ)=2×4r^2 ω^2 cos^2 θ+4r^2 ω^2 sin^2 θ g(((√3)/2)−cos θ)=rω^2 (1+cos^2 θ) ω^2 =((g(((√3)/2)−cos θ))/(r(1+cos^2 θ))) 2ω(dω/dθ)=(g/r)[((sin θ)/(1+cos^2 θ))+((2cos θ sin θ(((√3)/2)−cos θ))/((1+cos^2 θ)^2 ))] ω(dω/dθ)=((g sin θ(1+(√3)cos θ−cos^2 θ))/(2r(1+cos^2 θ)^2 )) A=(dU/dt)=2rω(−ω sin θ+cos θ (dω/dθ)) A=((g sin θ (cos^3 θ+3 cos θ−(√3)))/((1+cos^2 θ)^2 )) N sin θ=mA ⇒N=((mg (cos^3 θ+3 cos θ−(√3)))/((1+cos^2 θ)^2 )) N=0: cos^3 θ+3 cos θ−(√3)=0 cos θ=((((√7)+(√3))/2))^(1/3) −((((√7)−(√3))/2))^(1/3) =λ≈0.5282 U=cos θ(√((2((√3)−2cos θ))/(1+cos^2 θ)))(√(gr)) V=sin θ(√((2((√3)−2cos θ))/(1+cos^2 θ)))(√(gr)) dt=(dθ/ω)=(√((r(1+cos^2 θ))/(g(((√3)/2)−cos θ))))dθ T_1 =(√(r/g))∫_(π/6) ^θ (√((1+cos^2 θ)/(((√3)/2)−cos θ)))dθ T_1 =(√(r/g))∫_θ ^(π/6) (√((1+cos^2 θ)/((((√3)/2)−cos θ)(1−cos^2 θ))))d (cos θ) T_1 =(√(r/g))∫_λ ^((√3)/2) (√((1+ξ^2 )/((1−ξ^2 )(((√3)/2)−ξ))))dξ ≈2.36272(√(r/g)) h=r(1+2 cos θ) V_2 =(√(V^2 +2gh)) V_2 =(√(gr))(√(((2(1−cos^2 θ)((√3)−2cos θ))/(1+cos^2 θ))+2(1+2 cos θ))) ≈2.20741(√(gr)) T_2 =((V_2 −V)/g) T_2 =[(√(((2(1−cos^2 θ)((√3)−2cos θ))/(1+cos^2 θ))+2(1+2 cos θ)))−sin θ(√((2((√3)−2cos θ))/(1+cos^2 θ)))](√(r/g)) ≈1.33510(√(r/g)) T=T_1 +T_2 ≈3.69782(√(r/g)) camparation: free fall of the middle cylinder from same hight (1+(√3))r: V_2 =(√(2g(1+(√3))r))≈2.33754(√(gr)) T=(√((2(1+(√3))r)/g))≈2.33754(√(r/g))](Q214762.png)
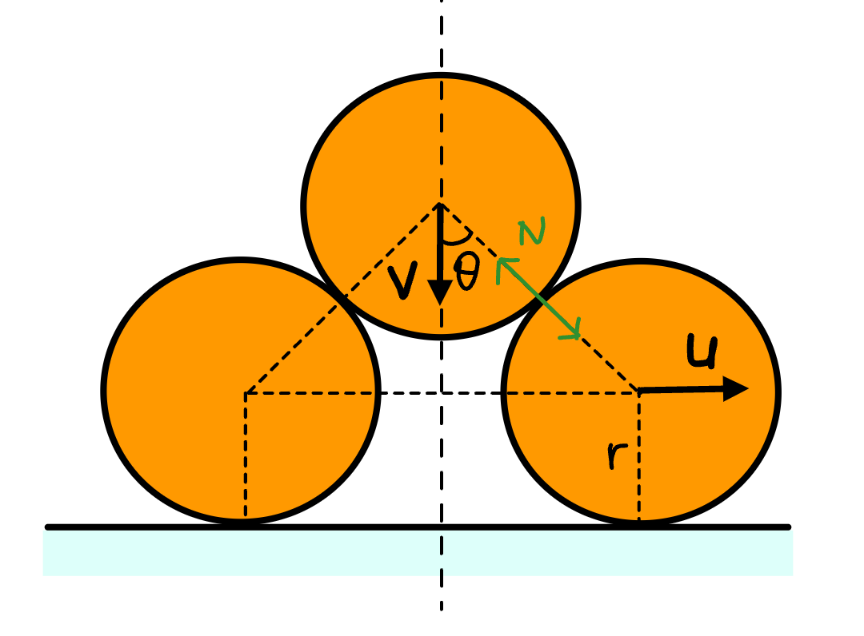
$${m}={mass}\:{of}\:{each}\:{cylinder} \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${X}=\mathrm{2}{r}\:\mathrm{sin}\:\theta \\ $$$${Y}=\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$${U}=\frac{{dX}}{{dt}}=\mathrm{2}{r}\omega\:\mathrm{cos}\:\theta \\ $$$${V}=−\frac{{dY}}{{dt}}=\mathrm{2}{r}\omega\:\mathrm{sin}\:\theta \\ $$$$\mathrm{2}{mgr}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{6}}−\mathrm{cos}\:\theta\right)=\mathrm{2}×\frac{{mU}^{\mathrm{2}} }{\mathrm{2}}+\frac{{mV}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{4}{gr}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)=\mathrm{2}×\mathrm{4}{r}^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{4}{r}^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$${g}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)={r}\omega^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right) \\ $$$$\omega^{\mathrm{2}} =\frac{{g}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)}{{r}\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)} \\ $$$$\mathrm{2}\omega\frac{{d}\omega}{{d}\theta}=\frac{{g}}{{r}}\left[\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}+\frac{\mathrm{2cos}\:\theta\:\mathrm{sin}\:\theta\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\right] \\ $$$$\omega\frac{{d}\omega}{{d}\theta}=\frac{{g}\:\mathrm{sin}\:\theta\left(\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta−\mathrm{cos}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{r}\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}=\frac{{dU}}{{dt}}=\mathrm{2}{r}\omega\left(−\omega\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\frac{{d}\omega}{{d}\theta}\right) \\ $$$${A}=\frac{{g}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{3}} \:\theta+\mathrm{3}\:\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\right)}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${N}\:\mathrm{sin}\:\theta={mA} \\ $$$$\Rightarrow{N}=\frac{{mg}\:\left(\mathrm{cos}^{\mathrm{3}} \:\theta+\mathrm{3}\:\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\right)}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${N}=\mathrm{0}: \\ $$$$\mathrm{cos}^{\mathrm{3}} \:\theta+\mathrm{3}\:\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta=\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}}{\mathrm{2}}}=\lambda\approx\mathrm{0}.\mathrm{5282} \\ $$$${U}=\mathrm{cos}\:\theta\sqrt{\frac{\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{2cos}\:\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}}\sqrt{{gr}} \\ $$$${V}=\mathrm{sin}\:\theta\sqrt{\frac{\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{2cos}\:\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}}\sqrt{{gr}} \\ $$$${dt}=\frac{{d}\theta}{\omega}=\sqrt{\frac{{r}\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right)}{{g}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)}}{d}\theta \\ $$$${T}_{\mathrm{1}} =\sqrt{\frac{{r}}{{g}}}\int_{\frac{\pi}{\mathrm{6}}} ^{\theta} \sqrt{\frac{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta}}{d}\theta \\ $$$${T}_{\mathrm{1}} =\sqrt{\frac{{r}}{{g}}}\int_{\theta} ^{\frac{\pi}{\mathrm{6}}} \sqrt{\frac{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\theta\right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)}}{d}\:\left(\mathrm{cos}\:\theta\right) \\ $$$${T}_{\mathrm{1}} =\sqrt{\frac{{r}}{{g}}}\int_{\lambda} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}+\xi^{\mathrm{2}} }{\left(\mathrm{1}−\xi^{\mathrm{2}} \right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\xi\right)}}{d}\xi \\ $$$$\:\:\:\:\approx\mathrm{2}.\mathrm{36272}\sqrt{\frac{{r}}{{g}}} \\ $$$${h}={r}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\theta\right) \\ $$$${V}_{\mathrm{2}} =\sqrt{{V}^{\mathrm{2}} +\mathrm{2}{gh}} \\ $$$${V}_{\mathrm{2}} =\sqrt{{gr}}\sqrt{\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)\left(\sqrt{\mathrm{3}}−\mathrm{2cos}\:\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}+\mathrm{2}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\theta\right)} \\ $$$$\:\:\:\:\:\approx\mathrm{2}.\mathrm{20741}\sqrt{{gr}} \\ $$$${T}_{\mathrm{2}} =\frac{{V}_{\mathrm{2}} −{V}}{{g}} \\ $$$${T}_{\mathrm{2}} =\left[\sqrt{\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)\left(\sqrt{\mathrm{3}}−\mathrm{2cos}\:\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}+\mathrm{2}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\theta\right)}−\mathrm{sin}\:\theta\sqrt{\frac{\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{2cos}\:\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}}\right]\sqrt{\frac{{r}}{{g}}} \\ $$$$\:\:\:\:\:\approx\mathrm{1}.\mathrm{33510}\sqrt{\frac{{r}}{{g}}} \\ $$$${T}={T}_{\mathrm{1}} +{T}_{\mathrm{2}} \approx\mathrm{3}.\mathrm{69782}\sqrt{\frac{{r}}{{g}}} \\ $$$$\underline{{camparation}:} \\ $$$${free}\:{fall}\:{of}\:{the}\:{middle}\:{cylinder} \\ $$$${from}\:{same}\:{hight}\:\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){r}: \\ $$$${V}_{\mathrm{2}} =\sqrt{\mathrm{2}{g}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){r}}\approx\mathrm{2}.\mathrm{33754}\sqrt{{gr}} \\ $$$${T}=\sqrt{\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){r}}{{g}}}\approx\mathrm{2}.\mathrm{33754}\sqrt{\frac{{r}}{{g}}} \\ $$
Commented by ajfour last updated on 20/Dec/24
https://youtube.com/shorts/iyQMnvfGLVI?si=T6BLqABWNk_2EqJT
Commented by mr W last updated on 20/Dec/24
��
