
Question Number 214536 by ajfour last updated on 11/Dec/24
Commented by ajfour last updated on 11/Dec/24

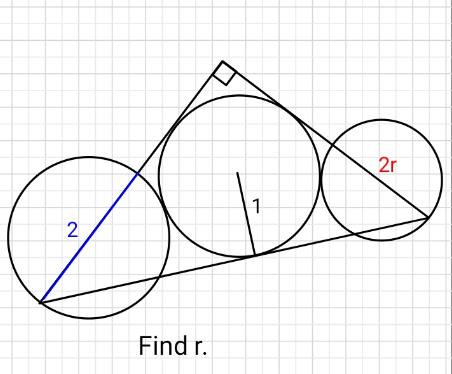
$${Out}\:{of}\:{questions}\:{labelled}\:{by}\:{just} \\ $$$${permutations}\:{of}\:{digits}\:{of}\:{the}\:{number} \\ $$$$\mathrm{123456}\:\:\:{what}\:{rank}\:{does}\:{this}\:{Q}\:{hold}? \\ $$$${In}\:{increasing}\:{order},\:{that}\:{is}. \\ $$
Commented by A5T last updated on 11/Dec/24

$$\overset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_} {{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} {x}_{\mathrm{4}} {x}_{\mathrm{5}} {x}_{\mathrm{6}} }\: \\ $$$${when}\:{x}_{\mathrm{1}} =\mathrm{1},\:{there}\:{are}\:\mathrm{5}!=\mathrm{120}\:{permutations}\:{of}\: \\ $$$$\left({x}_{\mathrm{2}} ,{x}_{\mathrm{3}} ,{x}_{\mathrm{4}} ,{x}_{\mathrm{5}} ,{x}_{\mathrm{6}} \right) \\ $$$${when}\:{x}_{\mathrm{1}} =\mathrm{2}\:{and}\:{x}_{\mathrm{2}} =\mathrm{1} \\ $$$${for}\:{x}_{\mathrm{3}} =\mathrm{3};\:{there}\:{are}\:\mathrm{3}!=\mathrm{6}\:{for}\:\left(\mathrm{4},\mathrm{5},\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{214356}\:−\:\left(\mathrm{120}+\mathrm{6}+\mathrm{1}\right){th} \\ $$$$\Rightarrow\mathrm{214365}\:−\:\mathrm{128}{th} \\ $$$$\Rightarrow\mathrm{214536}\:−\:\mathrm{129}{th} \\ $$
Commented by ajfour last updated on 12/Dec/24
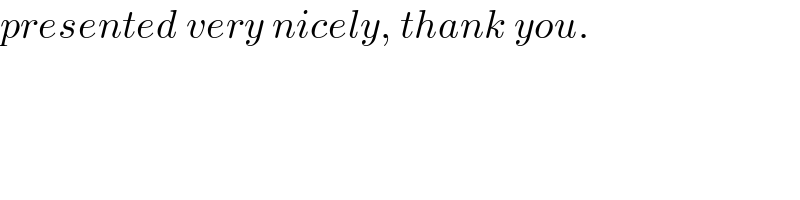
$${presented}\:{very}\:{nicely},\:{thank}\:{you}. \\ $$
Commented by ajfour last updated on 12/Dec/24
https://youtu.be/z2FHhUUw94A?si=WvWgazaVBulNRY9J
Answered by mr W last updated on 12/Dec/24
Commented by mr W last updated on 12/Dec/24
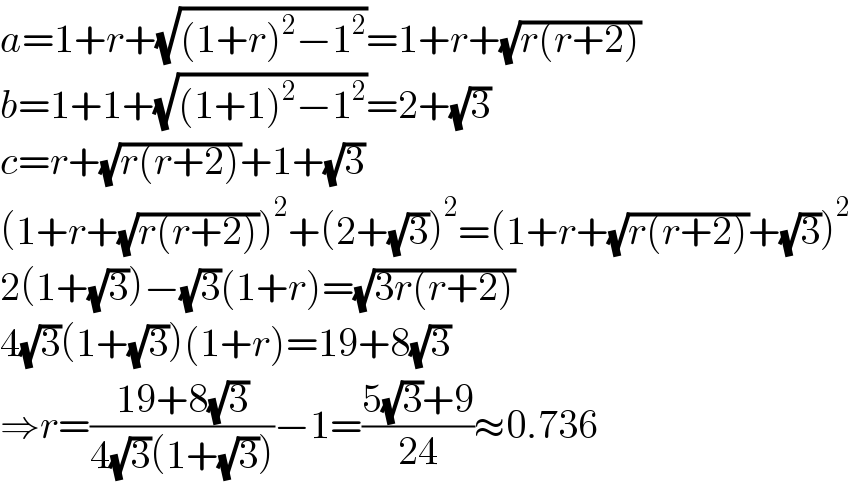
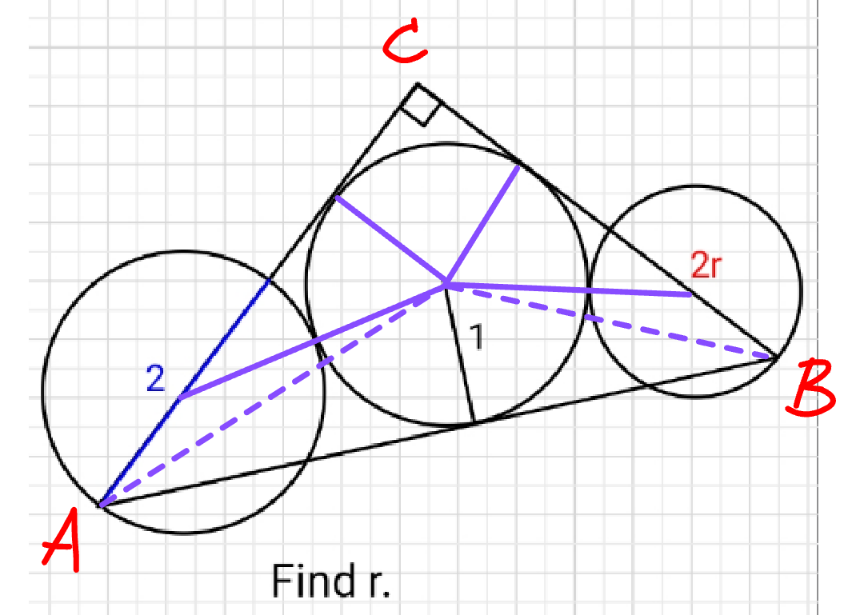
$${a}=\mathrm{1}+{r}+\sqrt{\left(\mathrm{1}+{r}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }=\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)} \\ $$$${b}=\mathrm{1}+\mathrm{1}+\sqrt{\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${c}={r}+\sqrt{{r}\left({r}+\mathrm{2}\right)}+\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)}\right)^{\mathrm{2}} +\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\left(\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)−\sqrt{\mathrm{3}}\left(\mathrm{1}+{r}\right)=\sqrt{\mathrm{3}{r}\left({r}+\mathrm{2}\right)} \\ $$$$\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+{r}\right)=\mathrm{19}+\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{19}+\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}−\mathrm{1}=\frac{\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{9}}{\mathrm{24}}\approx\mathrm{0}.\mathrm{736} \\ $$
Commented by ajfour last updated on 12/Dec/24

$${Wow}! \\ $$
Answered by A5T last updated on 11/Dec/24
Commented by A5T last updated on 11/Dec/24
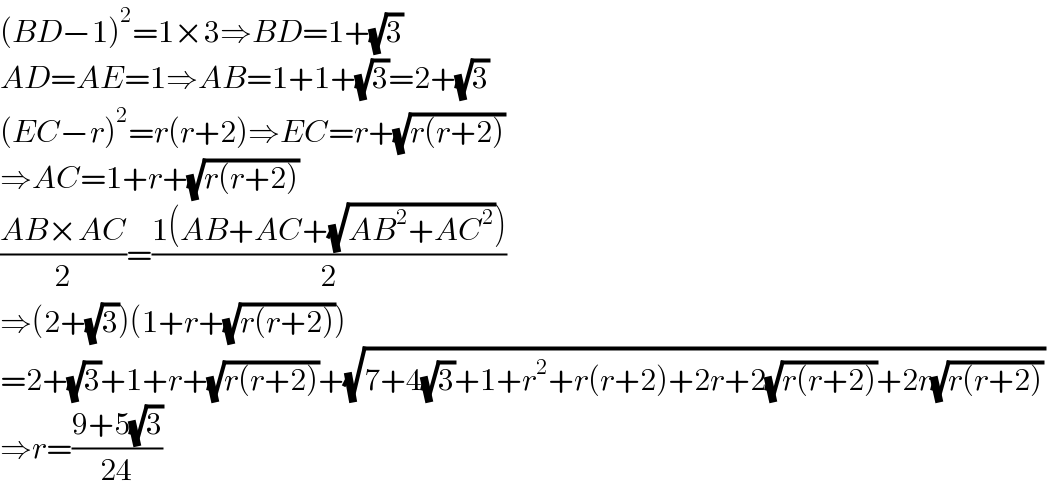
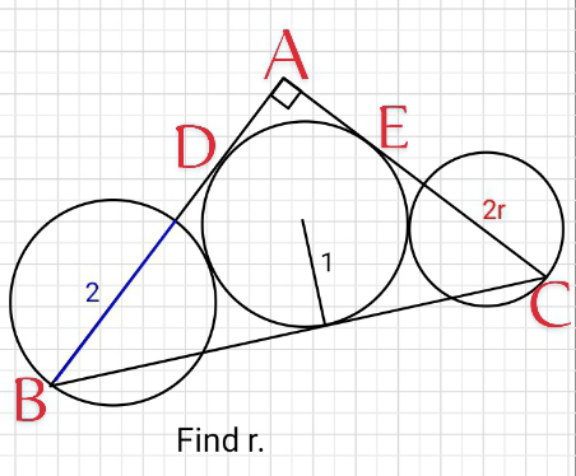
$$\left({BD}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}×\mathrm{3}\Rightarrow{BD}=\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$${AD}={AE}=\mathrm{1}\Rightarrow{AB}=\mathrm{1}+\mathrm{1}+\sqrt{\mathrm{3}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\left({EC}−{r}\right)^{\mathrm{2}} ={r}\left({r}+\mathrm{2}\right)\Rightarrow{EC}={r}+\sqrt{{r}\left({r}+\mathrm{2}\right)} \\ $$$$\Rightarrow{AC}=\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)} \\ $$$$\frac{{AB}×{AC}}{\mathrm{2}}=\frac{\mathrm{1}\left({AB}+{AC}+\sqrt{{AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} }\right)}{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)}\right) \\ $$$$=\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{1}+{r}+\sqrt{{r}\left({r}+\mathrm{2}\right)}+\sqrt{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{1}+{r}^{\mathrm{2}} +{r}\left({r}+\mathrm{2}\right)+\mathrm{2}{r}+\mathrm{2}\sqrt{{r}\left({r}+\mathrm{2}\right)}+\mathrm{2}{r}\sqrt{{r}\left({r}+\mathrm{2}\right)}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{9}+\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{24}} \\ $$
Commented by ajfour last updated on 11/Dec/24

$${Awesome}! \\ $$
