
Question Number 214498 by universe last updated on 10/Dec/24
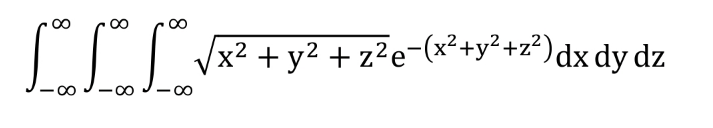
Answered by mr W last updated on 10/Dec/24
![=4π∫_0 ^∞ re^(−r^2 ) r^2 dr =2π∫_0 ^∞ pe^(−p) dp =2π(−pe^(−p) +∫_0 ^∞ e^(−p) dp) =2π[−pe^(−p) −e^(−p) ]_0 ^∞ =2π](Q214508.png)
$$=\mathrm{4}\pi\int_{\mathrm{0}} ^{\infty} {re}^{−{r}^{\mathrm{2}} } {r}^{\mathrm{2}} {dr} \\ $$$$=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} {pe}^{−{p}} {dp} \\ $$$$=\mathrm{2}\pi\left(−{pe}^{−{p}} +\int_{\mathrm{0}} ^{\infty} {e}^{−{p}} {dp}\right) \\ $$$$=\mathrm{2}\pi\left[−{pe}^{−{p}} −{e}^{−{p}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\mathrm{2}\pi \\ $$
Commented by universe last updated on 11/Dec/24
$${sorry}\:{sir}\:{i}\:{dont}\:{get}\:{it} \\ $$$${sir}\:{can}\:{you}\:{explain}\:{little}\:{bit}\: \\ $$
Commented by mr W last updated on 11/Dec/24
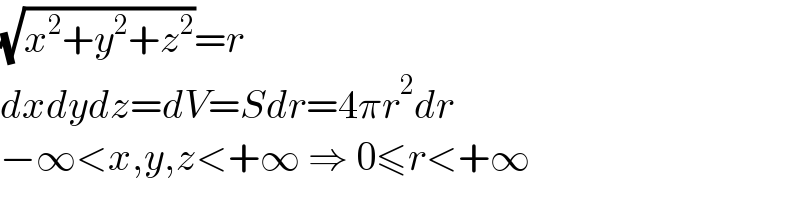
$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }={r} \\ $$$${dxdydz}={dV}={Sdr}=\mathrm{4}\pi{r}^{\mathrm{2}} {dr} \\ $$$$−\infty<{x},{y},{z}<+\infty\:\Rightarrow\:\mathrm{0}\leqslant{r}<+\infty \\ $$
Commented by universe last updated on 11/Dec/24
$${thank}\:{u}\:{so}\:{much}\:{sir} \\ $$
