
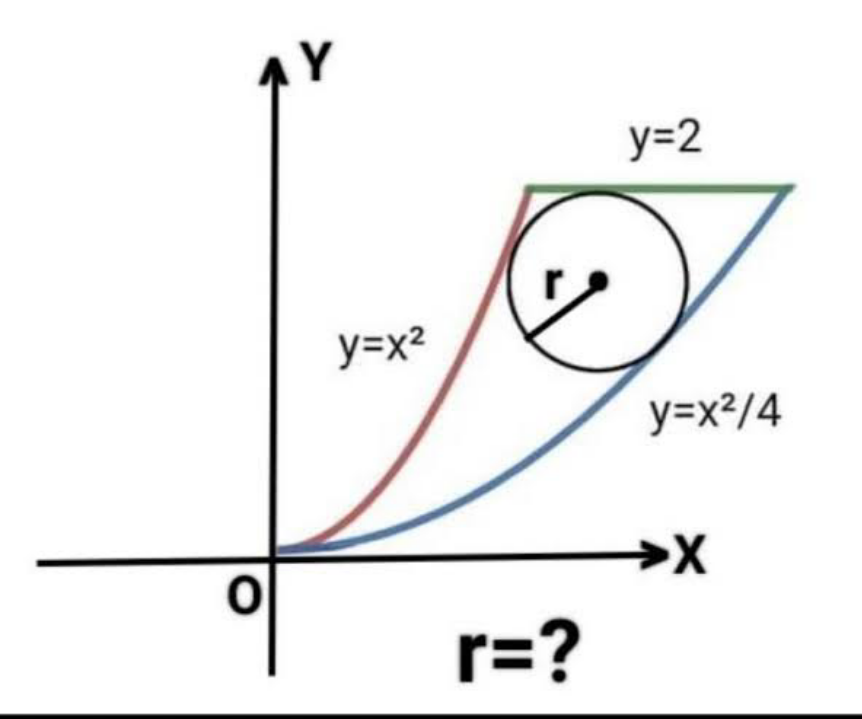
Question Number 214483 by MATHEMATICSAM last updated on 09/Dec/24
Answered by mr W last updated on 10/Dec/24

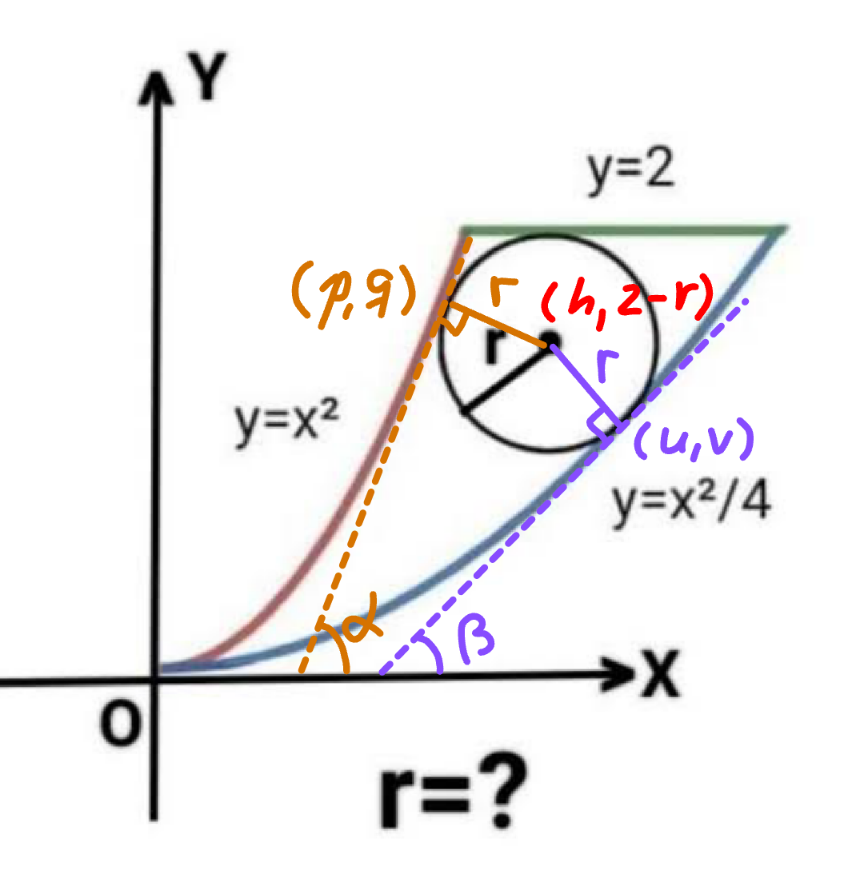
$${circle}\:{center}\:{at}\:\left({h},\:\mathrm{2}−{r}\right) \\ $$$${touching}\:{y}={x}^{\mathrm{2}} \:{at}\:\left({p},\:{q}\right) \\ $$$${q}={p}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{p}=\mathrm{tan}\:\alpha \\ $$$${h}={p}+{r}\:\mathrm{sin}\:\alpha={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\mathrm{2}−{r}={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\alpha={p}^{\mathrm{2}} −\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\mathrm{2}−{p}^{\mathrm{2}} ={r}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right) \\ $$$$\begin{cases}{{r}=\frac{\mathrm{2}−{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}}\\{{h}={p}+\frac{\mathrm{2}{p}\left(\mathrm{2}−{p}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }−\mathrm{1}}}\end{cases}\:\:\:\:\:\:...\left({I}\right) \\ $$$${touching}\:{y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{at}\:\left({u},\:{v}\right) \\ $$$${v}=\frac{{u}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{u}}{\mathrm{2}}=\mathrm{tan}\:\beta \\ $$$${h}={u}−{r}\:\mathrm{sin}\:\beta={u}−\frac{{ur}}{\mathrm{2}\sqrt{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$$\mathrm{2}−{r}=\frac{{u}^{\mathrm{2}} }{\mathrm{4}}+{r}\:\mathrm{cos}\:\beta=\frac{{u}^{\mathrm{2}} }{\mathrm{4}}+\frac{{r}}{\:\sqrt{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$$\begin{cases}{{r}=\frac{\mathrm{2}−\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}}}}\\{{h}={u}−\frac{{u}\left(\mathrm{2}−\frac{{u}^{\mathrm{2}} }{\mathrm{4}}\right)}{\mathrm{2}\left(\sqrt{\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{4}}}+\mathrm{1}\right)}}\end{cases}\:\:\:...\left({II}\right) \\ $$$${intersection}\:{of}\:{both}\:{parameterised} \\ $$$${curves}\:{is}\:{at} \\ $$$${h}\approx\mathrm{1}.\mathrm{76833} \\ $$$${r}\approx\mathrm{0}.\mathrm{50832}\:\checkmark \\ $$
Commented by TonyCWX08 last updated on 10/Dec/24

$${May}\:{I}\:{know}\:{why}\:{there}\:{is}\:{an}\:{angle}\:{there}? \\ $$$${I}\:{don}'{t}\:{see}\:{the}\:\alpha\:{and}\:\beta... \\ $$
Commented by mr W last updated on 10/Dec/24
Commented by mr W last updated on 10/Dec/24
Commented by TonyCWX08 last updated on 11/Dec/24

$${Where}\:{can}\:{I}\:{actually}\:{learn}\:{all}\:{these}\:{stuffs}?? \\ $$
Commented by ajfour last updated on 11/Dec/24
You cant find heaven anywhere other than where you are.��
Commented by mr W last updated on 11/Dec/24

$${To}\:{learn}\:{things}\:{is}\:{one}\:{thing},\:{to} \\ $$$${apply}\:{the}\:{things}\:{learnt}\:{is}\:{an}\:{other} \\ $$$${thing}! \\ $$$${Perhaps}\:{you}\:{have}\:{already}\:{learnt} \\ $$$${all}\:{the}\:{stuff}\:{concerned}\:{in}\:{this}\: \\ $$$${question},\:{you}\:{only}\:{need}\:{to}\:{apply} \\ $$$${it}. \\ $$
