
Question Number 214449 by ajfour last updated on 08/Dec/24
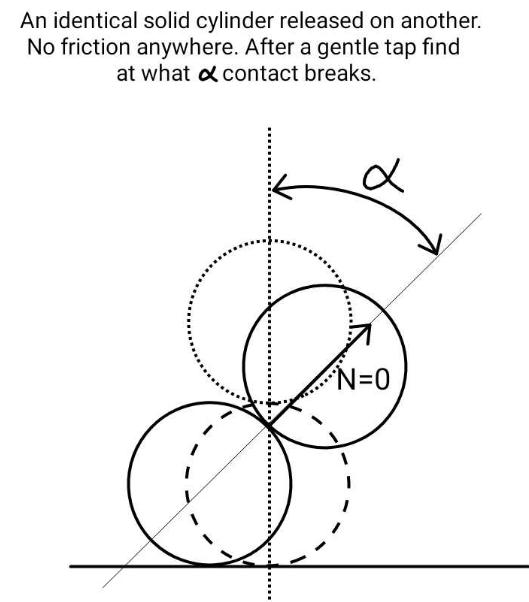
Commented by ajfour last updated on 09/Dec/24
https://youtu.be/mVW8FiNpKjk?si=q68kdETxCuqwyZ3-
Answered by mr W last updated on 14/Dec/24
Commented by mr W last updated on 15/Dec/24
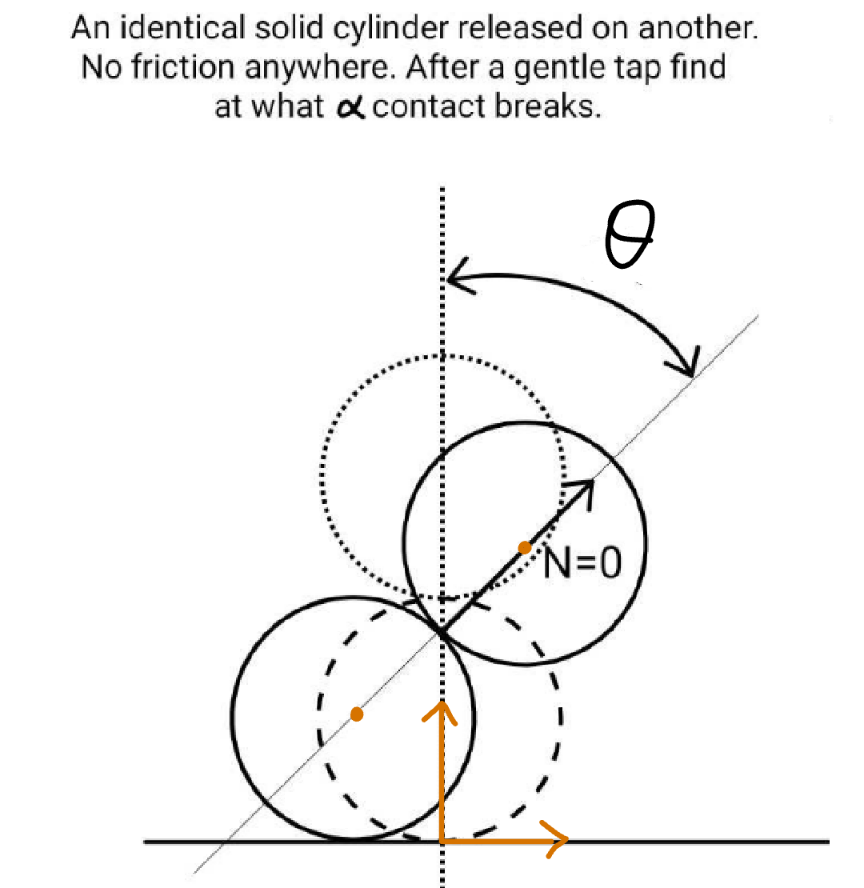
![(X, Y) =center of lower cylinder (x, y) =center of upper cylinder X=−r sin θ Y=r x=r sin θ y=r+2r cos θ let ω=(dθ/dt) V_x =−(dX/dt)=ωr cos θ V_y =0 v_x =(dx/dt)=ωr cos θ v_y =−(dy/dt)=2ωr sin θ both cylinders obtain no rotation. 2mgr(1−cos θ)=((mω^2 r^2 cos^2 θ)/2)+((mω^2 r^2 (cos^2 θ+4 sin^2 θ))/2) 2g(1−cos θ)=ω^2 r(1+sin^2 θ) ⇒ω^2 =((2g(1−cos θ))/(r(1+sin^2 θ))) 2ω(dω/dθ)=((2g)/r)[((sin θ)/(1+sin^2 θ))−((2(1−cos θ) sin θ cos θ)/((1+sin^2 θ)^2 ))] ω(dω/dθ)=((g sin θ (cos^2 θ−2 cos θ+2))/(r(1+sin^2 θ)^2 )) A_x =(dV_x /dt)=ω(dV_x /dθ)=ωr(−ω sin θ+cos θ (dω/dθ)) A_x =g[−((2 sin θ(1−cos θ))/((1+sin^2 θ)))+((sin θ cos θ(cos^2 θ−2 cos θ+2))/((1+sin^2 θ)^2 ))] A_x =((g sin θ(−cos^3 θ+6 cos θ−4))/((1+sin^2 θ)^2 )) N sin θ=mA_x ⇒(N/(mg))=((−cos^3 θ+6 cos θ−4)/((1+sin^2 θ)^2 )) when N=0, cos^3 θ−6 cos θ+4=0 (cos θ−2)(cos^2 θ+2 cos θ−2)=0 0<cos θ<1 ⇒only one root is suitable cos θ=(√3)−1 ⇒θ=cos^(−1) ((√3)−1)≈42.941° ================== V_x =ωr cos θ=cos θ(√((2gr(1−cos θ))/(1+sin^2 θ))) V_(x,final) =(√((3(√3)−5)gr))≈0.4429(√(gr)) this is the final speed of the lower cylinder after separation from the upper cylinder.](Q214654.png)
$$\left({X},\:{Y}\right)\:={center}\:{of}\:{lower}\:{cylinder} \\ $$$$\left({x},\:{y}\right)\:={center}\:{of}\:{upper}\:{cylinder} \\ $$$${X}=−{r}\:\mathrm{sin}\:\theta \\ $$$${Y}={r} \\ $$$${x}={r}\:\mathrm{sin}\:\theta \\ $$$${y}={r}+\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$${let}\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${V}_{{x}} =−\frac{{dX}}{{dt}}=\omega{r}\:\mathrm{cos}\:\theta \\ $$$${V}_{{y}} =\mathrm{0} \\ $$$${v}_{{x}} =\frac{{dx}}{{dt}}=\omega{r}\:\mathrm{cos}\:\theta \\ $$$${v}_{{y}} =−\frac{{dy}}{{dt}}=\mathrm{2}\omega{r}\:\mathrm{sin}\:\theta \\ $$$${both}\:{cylinders}\:{obtain}\:{no}\:{rotation}. \\ $$$$\mathrm{2}{mgr}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\frac{{m}\omega^{\mathrm{2}} {r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{2}}+\frac{{m}\omega^{\mathrm{2}} {r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}} \\ $$$$\mathrm{2}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\omega^{\mathrm{2}} {r}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right) \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{{r}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)} \\ $$$$\mathrm{2}\omega\frac{{d}\omega}{{d}\theta}=\frac{\mathrm{2}{g}}{{r}}\left[\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta}−\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\right] \\ $$$$\omega\frac{{d}\omega}{{d}\theta}=\frac{{g}\:\mathrm{sin}\:\theta\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\mathrm{2}\right)}{{r}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}_{{x}} =\frac{{dV}_{{x}} }{{dt}}=\omega\frac{{dV}_{{x}} }{{d}\theta}=\omega{r}\left(−\omega\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\frac{{d}\omega}{{d}\theta}\right) \\ $$$${A}_{{x}} ={g}\left[−\frac{\mathrm{2}\:\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)}+\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\:\mathrm{cos}\:\theta+\mathrm{2}\right)}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\right] \\ $$$${A}_{{x}} =\frac{{g}\:\mathrm{sin}\:\theta\left(−\mathrm{cos}^{\mathrm{3}} \:\theta+\mathrm{6}\:\mathrm{cos}\:\theta−\mathrm{4}\right)}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${N}\:\mathrm{sin}\:\theta={mA}_{{x}} \\ $$$$\Rightarrow\frac{{N}}{{mg}}=\frac{−\mathrm{cos}^{\mathrm{3}} \:\theta+\mathrm{6}\:\mathrm{cos}\:\theta−\mathrm{4}}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${when}\:{N}=\mathrm{0}, \\ $$$$\mathrm{cos}^{\mathrm{3}} \:\theta−\mathrm{6}\:\mathrm{cos}\:\theta+\mathrm{4}=\mathrm{0} \\ $$$$\left(\mathrm{cos}\:\theta−\mathrm{2}\right)\left(\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{0}<\mathrm{cos}\:\theta<\mathrm{1}\:\Rightarrow{only}\:{one}\:{root}\:{is}\:{suitable} \\ $$$$\mathrm{cos}\:\theta=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\approx\mathrm{42}.\mathrm{941}° \\ $$$$================== \\ $$$${V}_{{x}} =\omega{r}\:\mathrm{cos}\:\theta=\mathrm{cos}\:\theta\sqrt{\frac{\mathrm{2}{gr}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$${V}_{{x},{final}} =\sqrt{\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}\right){gr}}\approx\mathrm{0}.\mathrm{4429}\sqrt{{gr}} \\ $$$${this}\:{is}\:{the}\:{final}\:{speed}\:{of}\:{the}\:{lower} \\ $$$${cylinder}\:{after}\:{separation}\:{from}\:{the} \\ $$$${upper}\:{cylinder}. \\ $$
Commented by ajfour last updated on 15/Dec/24
Really glad for the same conclusion, sir.
Answered by ajfour last updated on 09/Dec/24
Commented by ajfour last updated on 04/Jan/25
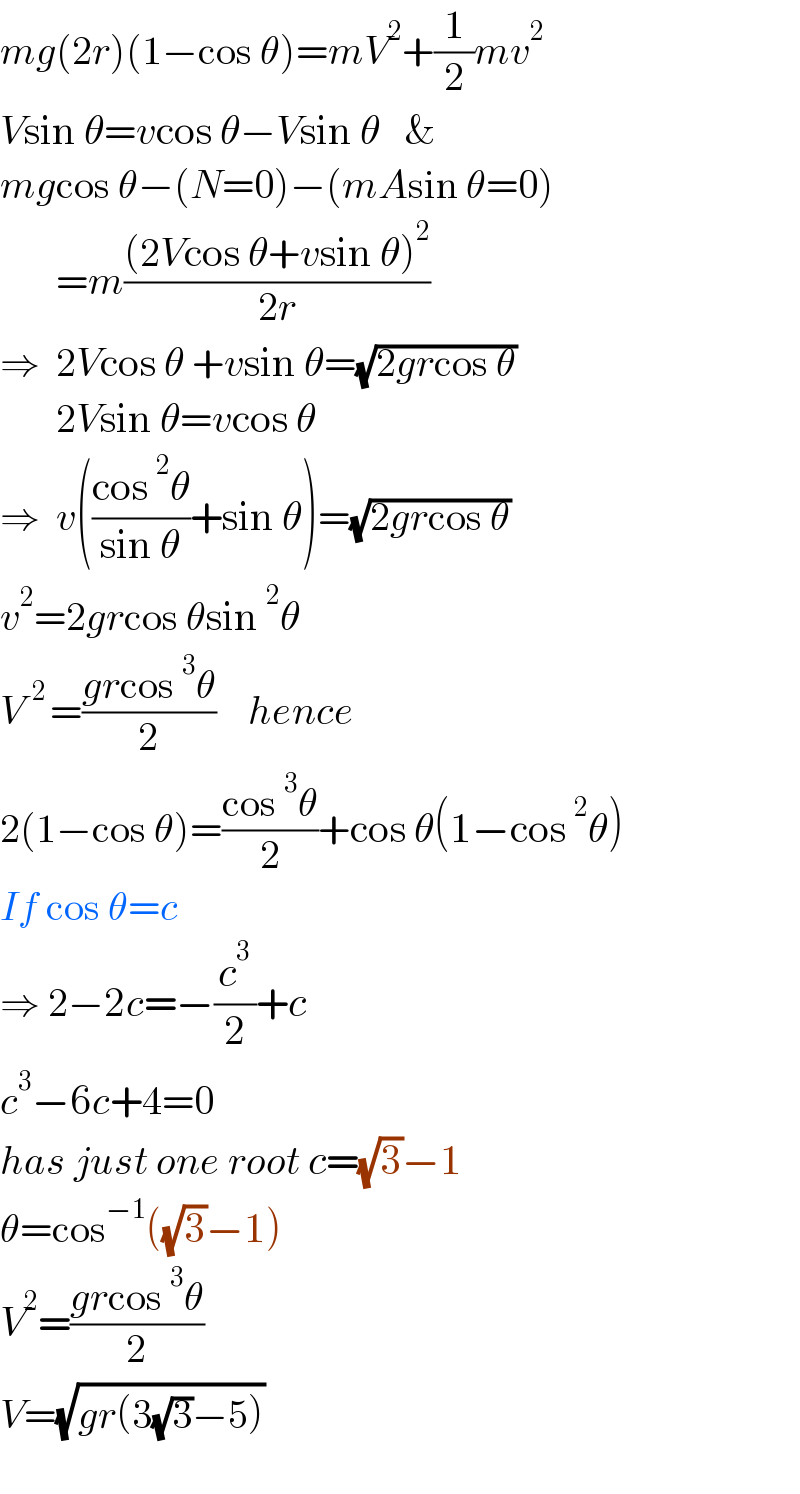
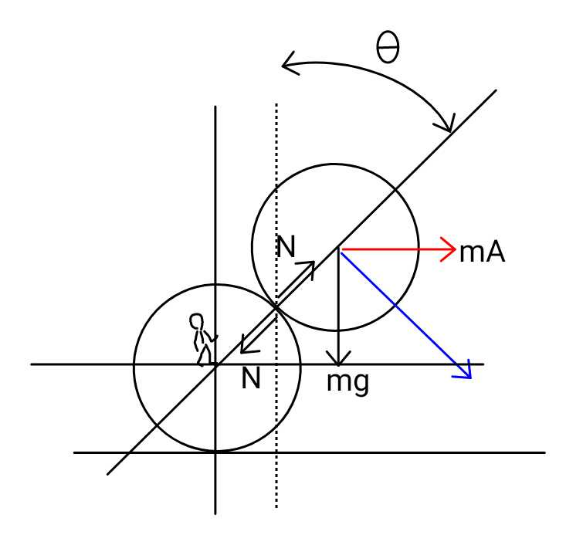
$${mg}\left(\mathrm{2}{r}\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)={mV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$${V}\mathrm{sin}\:\theta={v}\mathrm{cos}\:\theta−{V}\mathrm{sin}\:\theta\:\:\:\& \\ $$$${mg}\mathrm{cos}\:\theta−\left({N}=\mathrm{0}\right)−\left({mA}\mathrm{sin}\:\theta=\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:={m}\frac{\left(\mathrm{2}{V}\mathrm{cos}\:\theta+{v}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{\mathrm{2}{r}} \\ $$$$\Rightarrow\:\:\mathrm{2}{V}\mathrm{cos}\:\theta\:+{v}\mathrm{sin}\:\theta=\sqrt{\mathrm{2}{gr}\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}{V}\mathrm{sin}\:\theta={v}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{v}\left(\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta}+\mathrm{sin}\:\theta\right)=\sqrt{\mathrm{2}{gr}\mathrm{cos}\:\theta} \\ $$$${v}^{\mathrm{2}} =\mathrm{2}{gr}\mathrm{cos}\:\theta\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${V}^{\:\:\mathrm{2}\:} =\frac{{gr}\mathrm{cos}\:^{\mathrm{3}} \theta}{\mathrm{2}}\:\:\:\:{hence} \\ $$$$\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\frac{\mathrm{cos}\:^{\mathrm{3}} \theta}{\mathrm{2}}+\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$${If}\:\mathrm{cos}\:\theta={c} \\ $$$$\Rightarrow\:\mathrm{2}−\mathrm{2}{c}=−\frac{{c}^{\mathrm{3}} }{\mathrm{2}}+{c} \\ $$$${c}^{\mathrm{3}} −\mathrm{6}{c}+\mathrm{4}=\mathrm{0} \\ $$$${has}\:{just}\:{one}\:{root}\:{c}=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\: \\ $$$${V}^{\mathrm{2}} =\frac{{gr}\mathrm{cos}\:^{\mathrm{3}} \theta}{\mathrm{2}} \\ $$$${V}=\sqrt{{gr}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}\right)} \\ $$$$ \\ $$
Commented by ajfour last updated on 09/Dec/24
https://youtu.be/pHHTfPtRV98?si=JtR34MdARBkxuPIV
