Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

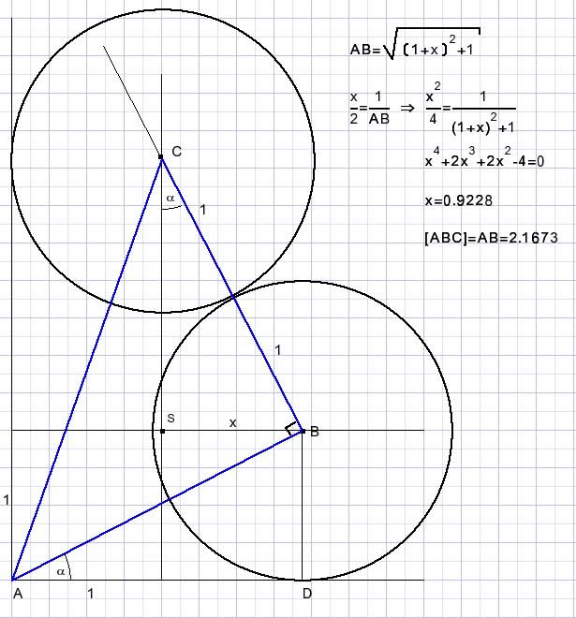
Question Number 214427 by ajfour last updated on 08/Dec/24

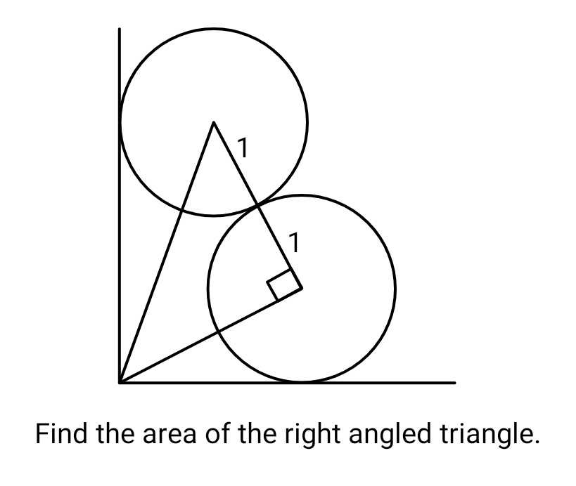
Commented by ajfour last updated on 08/Dec/24

https://youtu.be/pnMSZ77i2P8?si=OaLd0p_DlkwNYv8d

Answered by a.lgnaoui last updated on 08/Dec/24

Resolution de l equation donne x=0,60048518 alors Aire=x+1=1,60048518 autre Methode Aire= Aire[Care( OAED)]=1 2Aire(OEC)=2×(x/2)=x A=A(Care)+2A(OEC)=x+1

$$\mathrm{Resolution}\:\mathrm{de}\:\mathrm{l}\:\mathrm{equation}\:\mathrm{donne} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{0},\mathrm{60048518} \\ $$$$\mathrm{alors}\:\:\:\:\boldsymbol{\mathrm{Aire}}=\boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{1},\mathrm{60048518} \\ $$$$ \\ $$$$\mathrm{autre}\:\mathrm{Methode} \\ $$$$\:\mathrm{Aire}=\:\mathrm{Aire}\left[\mathrm{Care}\left(\:\mathrm{OAED}\right)\right]=\mathrm{1} \\ $$$$\mathrm{2Aire}\left(\mathrm{OEC}\right)=\mathrm{2}×\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{x} \\ $$$$\mathrm{A}=\mathrm{A}\left(\mathrm{Care}\right)+\mathrm{2A}\left(\mathrm{OEC}\right)=\mathrm{x}+\mathrm{1} \\ $$$$\:\: \\ $$

Commented by a.lgnaoui last updated on 08/Dec/24

Commented by a.lgnaoui last updated on 08/Dec/24

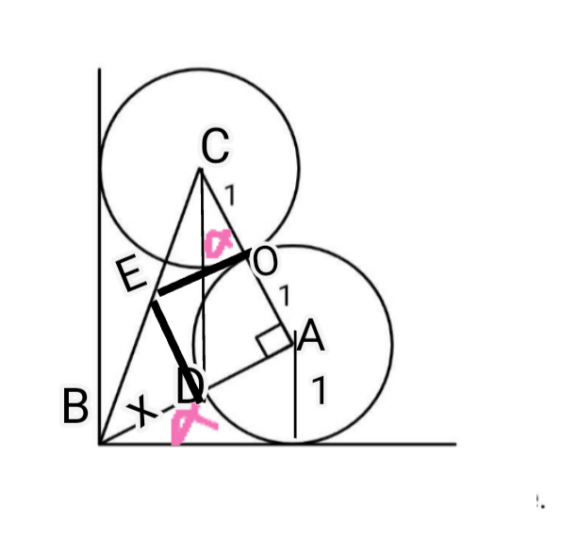
Commented by mr W last updated on 08/Dec/24

clearly wrong! even from the diagram one can see that your x should be ≈ 1 and >1. so your answer x=0,60048518 is wrong.

$${clearly}\:{wrong}!\:{even}\:{from}\:{the} \\ $$$${diagram}\:{one}\:{can}\:{see}\:{that}\:{your}\:{x} \\ $$$${should}\:{be}\:\approx\:\mathrm{1}\:{and}\:>\mathrm{1}.\:{so}\:{your}\:{answer} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{0},\mathrm{60048518}\:{is}\:{wrong}. \\ $$

Answered by mr W last updated on 08/Dec/24

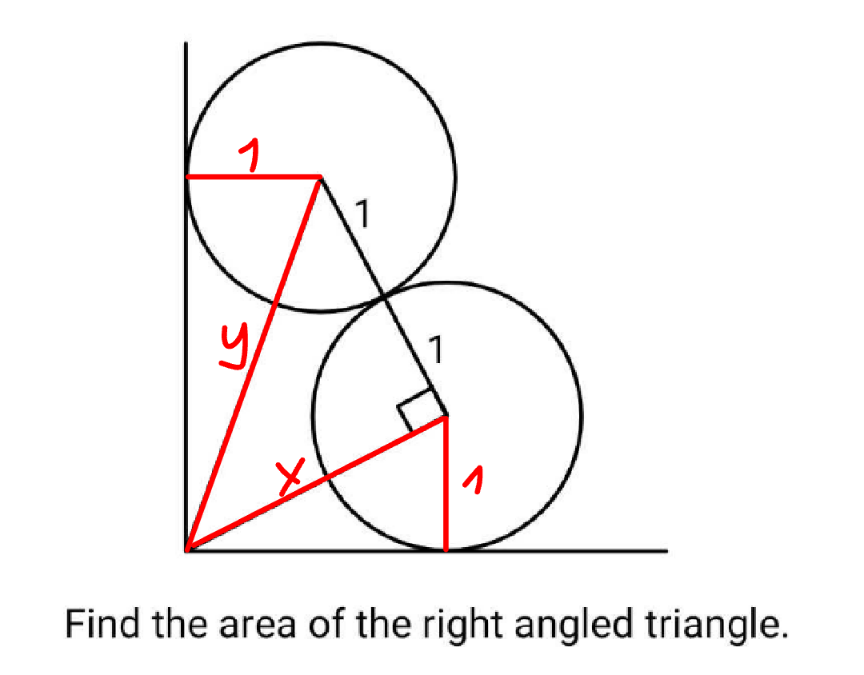
Commented by mr W last updated on 08/Dec/24

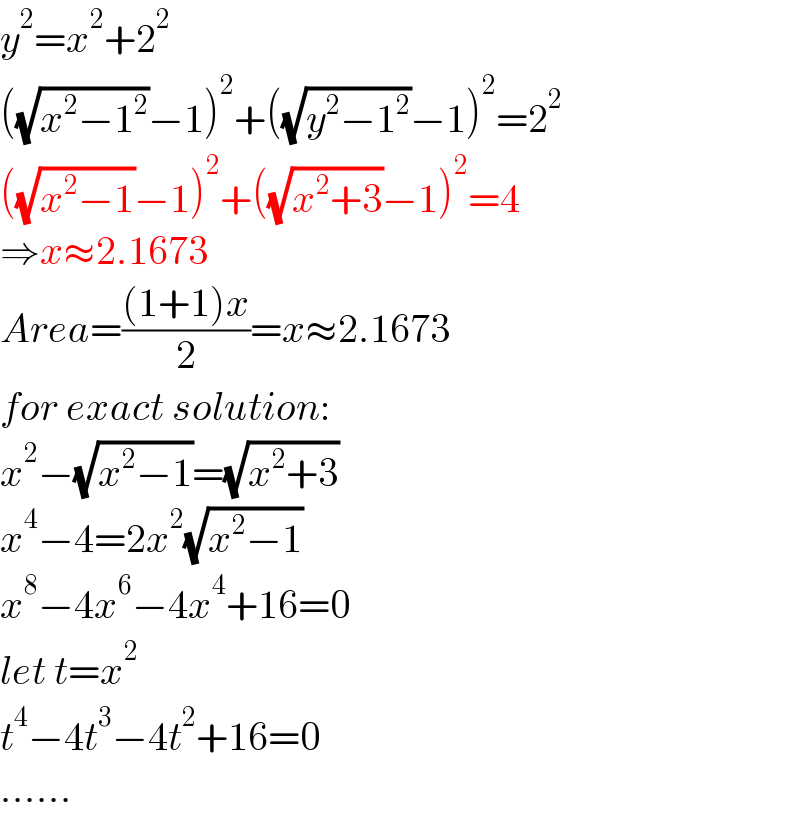
y^2 =x^2 +2^2 ((√(x^2 −1^2 ))−1)^2 +((√(y^2 −1^2 ))−1)^2 =2^2 ((√(x^2 −1))−1)^2 +((√(x^2 +3))−1)^2 =4 ⇒x≈2.1673 Area=(((1+1)x)/2)=x≈2.1673 for exact solution: x^2 −(√(x^2 −1))=(√(x^2 +3)) x^4 −4=2x^2 (√(x^2 −1)) x^8 −4x^6 −4x^4 +16=0 let t=x^2 t^4 −4t^3 −4t^2 +16=0 ......

$${y}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \\ $$$$\left(\sqrt{{x}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }−\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\left(\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow{x}\approx\mathrm{2}.\mathrm{1673} \\ $$$${Area}=\frac{\left(\mathrm{1}+\mathrm{1}\right){x}}{\mathrm{2}}={x}\approx\mathrm{2}.\mathrm{1673} \\ $$$${for}\:{exact}\:{solution}: \\ $$$${x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$${x}^{\mathrm{4}} −\mathrm{4}=\mathrm{2}{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${x}^{\mathrm{8}} −\mathrm{4}{x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{16}=\mathrm{0} \\ $$$${let}\:{t}={x}^{\mathrm{2}} \\ $$$${t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$$...... \\ $$

Commented by ajfour last updated on 08/Dec/24

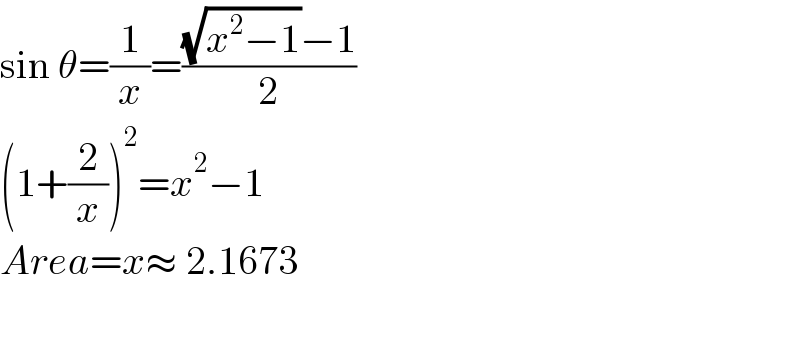
sin θ=(1/x)=(((√(x^2 −1))−1)/2) (1+(2/x))^2 =x^2 −1 Area=x≈ 2.1673

$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{{x}}=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{1} \\ $$$${Area}={x}\approx\:\mathrm{2}.\mathrm{1673}\: \\ $$$$ \\ $$

Answered by Spillover last updated on 11/Dec/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com