Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 214409 by ajfour last updated on 07/Dec/24

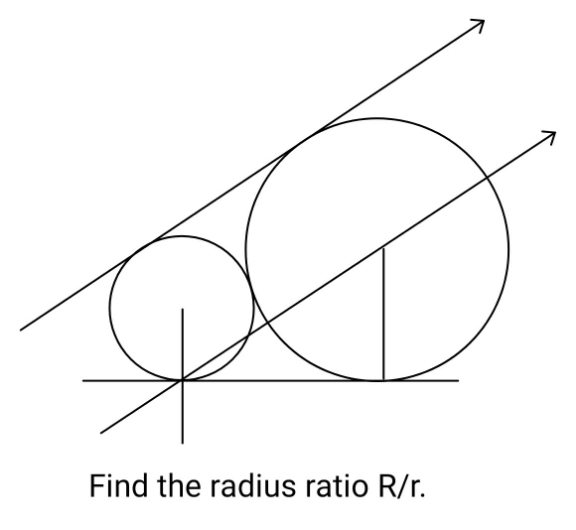
Answered by A5T last updated on 07/Dec/24

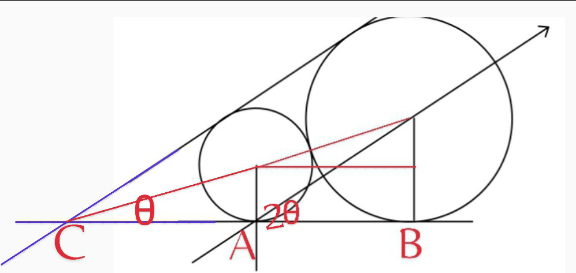
Commented by A5T last updated on 07/Dec/24

AB=(√((r+R)^2 −(R−r)^2 ))=2(√(rR)) ⇒tan2θ=((2tanθ)/(1−tan^2 θ))=(R/(2(√(rR))))=(1/2)(√(R/r))=p ⇒ptan^2 θ+2tanθ−p=0 ⇒tanθ=((−2+_− (√(4+4p^2 )))/(2p))=((−2(√r)+_− (√(4r+R)))/( (√R))) For θ<90; tanθ=(((√(4r+R))−2(√r))/( (√R)))=(r/(AC)) ⇒AC=((r(√R))/( (√(4r+R))−2(√r))) (R/r)=((BC=BA+AC)/(AC))=((BA)/(AC))+1=((2(√(4r^2 +Rr))−3r)/r) ⇒(R+3r)^2 =4(4r^2 +Rr)⇒R^2 +2Rr=7r^2 ⇒^(/r^2 ) ((R/r))^2 +2((R/r))−7=0⇒(R/r)=((−2+_− (√(4+28)))/2) (R/r)>0⇒(R/r)=((4(√2)−2)/2)=2(√2)−1

$${AB}=\sqrt{\left({r}+{R}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{rR}} \\ $$$$\Rightarrow{tan}\mathrm{2}\theta=\frac{\mathrm{2}{tan}\theta}{\mathrm{1}−{tan}^{\mathrm{2}} \theta}=\frac{{R}}{\mathrm{2}\sqrt{{rR}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{R}}{{r}}}={p} \\ $$$$\Rightarrow{ptan}^{\mathrm{2}} \theta+\mathrm{2}{tan}\theta−{p}=\mathrm{0} \\ $$$$\Rightarrow{tan}\theta=\frac{−\mathrm{2}\underset{−} {+}\sqrt{\mathrm{4}+\mathrm{4}{p}^{\mathrm{2}} }}{\mathrm{2}{p}}=\frac{−\mathrm{2}\sqrt{{r}}\underset{−} {+}\sqrt{\mathrm{4}{r}+{R}}}{\:\sqrt{{R}}} \\ $$$${For}\:\theta<\mathrm{90};\:{tan}\theta=\frac{\sqrt{\mathrm{4}{r}+{R}}−\mathrm{2}\sqrt{{r}}}{\:\sqrt{{R}}}=\frac{{r}}{{AC}} \\ $$$$\Rightarrow{AC}=\frac{{r}\sqrt{{R}}}{\:\sqrt{\mathrm{4}{r}+{R}}−\mathrm{2}\sqrt{{r}}} \\ $$$$\frac{{R}}{{r}}=\frac{{BC}={BA}+{AC}}{{AC}}=\frac{{BA}}{{AC}}+\mathrm{1}=\frac{\mathrm{2}\sqrt{\mathrm{4}{r}^{\mathrm{2}} +{Rr}}−\mathrm{3}{r}}{{r}} \\ $$$$\Rightarrow\left({R}+\mathrm{3}{r}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{4}{r}^{\mathrm{2}} +{Rr}\right)\Rightarrow{R}^{\mathrm{2}} +\mathrm{2}{Rr}=\mathrm{7}{r}^{\mathrm{2}} \\ $$$$\overset{/{r}^{\mathrm{2}} } {\Rightarrow}\left(\frac{{R}}{{r}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{R}}{{r}}\right)−\mathrm{7}=\mathrm{0}\Rightarrow\frac{{R}}{{r}}=\frac{−\mathrm{2}\underset{−} {+}\sqrt{\mathrm{4}+\mathrm{28}}}{\mathrm{2}} \\ $$$$\frac{{R}}{{r}}>\mathrm{0}\Rightarrow\frac{{R}}{{r}}=\frac{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1} \\ $$

Commented by ajfour last updated on 07/Dec/24

wow super good!

$${wow}\:{super}\:{good}! \\ $$

Answered by mr W last updated on 07/Dec/24

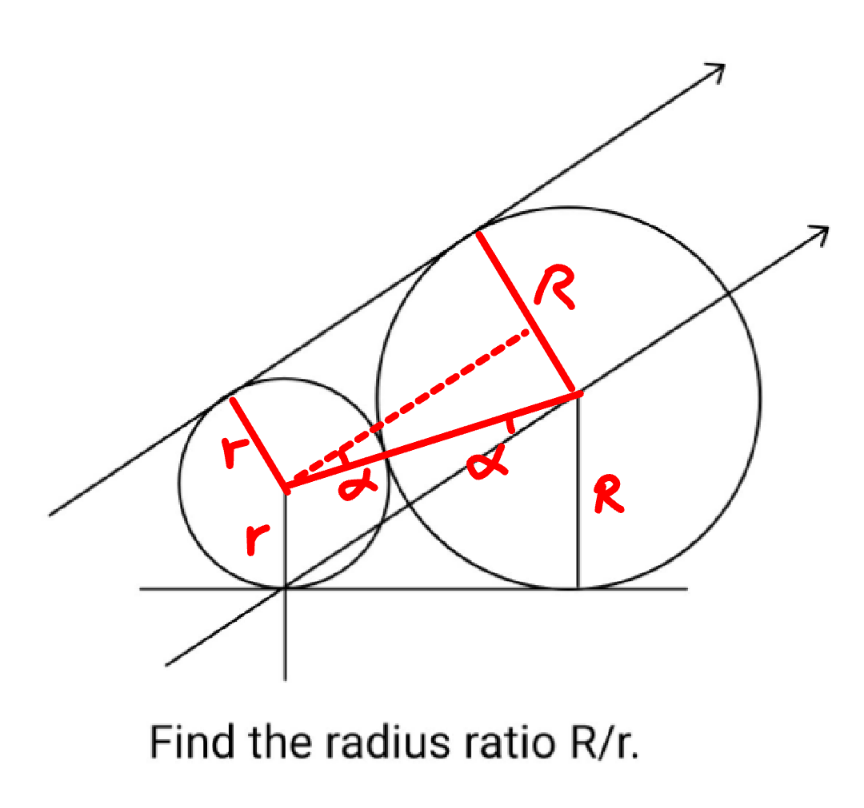
Commented by mr W last updated on 07/Dec/24

let λ=(R/r) sin α=((R−r)/(R+r))=((λ−1)/(λ+1)) cos α=(((R+r)^2 +4Rr+R^2 −r^2 )/(2(R+r)(√(4Rr+R^2 )))) =((R^2 +3Rr)/((R+r)(√(4Rr+R^2 ))))=(((λ+3)λ)/((λ+1)(√(λ^2 +4λ)))) (((λ−1)/(λ+1)))^2 +[(((λ+3)λ)/((λ+1)(√(λ^2 +4λ))))]^2 =1 [(((λ+3)λ)/( (√(λ^2 +4λ))))]^2 =(λ+1)^2 −(λ−1)^2 =4λ λ^2 +2λ−7=0 ⇒λ=2(√2)−1 ✓

$${let}\:\lambda=\frac{{R}}{{r}} \\ $$$$\mathrm{sin}\:\alpha=\frac{{R}−{r}}{{R}+{r}}=\frac{\lambda−\mathrm{1}}{\lambda+\mathrm{1}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\left({R}+{r}\right)^{\mathrm{2}} +\mathrm{4}{Rr}+{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}\left({R}+{r}\right)\sqrt{\mathrm{4}{Rr}+{R}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{{R}^{\mathrm{2}} +\mathrm{3}{Rr}}{\left({R}+{r}\right)\sqrt{\mathrm{4}{Rr}+{R}^{\mathrm{2}} }}=\frac{\left(\lambda+\mathrm{3}\right)\lambda}{\left(\lambda+\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{4}\lambda}} \\ $$$$\left(\frac{\lambda−\mathrm{1}}{\lambda+\mathrm{1}}\right)^{\mathrm{2}} +\left[\frac{\left(\lambda+\mathrm{3}\right)\lambda}{\left(\lambda+\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{4}\lambda}}\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\left[\frac{\left(\lambda+\mathrm{3}\right)\lambda}{\:\sqrt{\lambda^{\mathrm{2}} +\mathrm{4}\lambda}}\right]^{\mathrm{2}} =\left(\lambda+\mathrm{1}\right)^{\mathrm{2}} −\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\lambda \\ $$$$\lambda^{\mathrm{2}} +\mathrm{2}\lambda−\mathrm{7}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\:\checkmark \\ $$

Commented by ajfour last updated on 08/Dec/24

great way! Sir.

$${great}\:{way}!\:{Sir}. \\ $$

Commented by ajfour last updated on 08/Dec/24

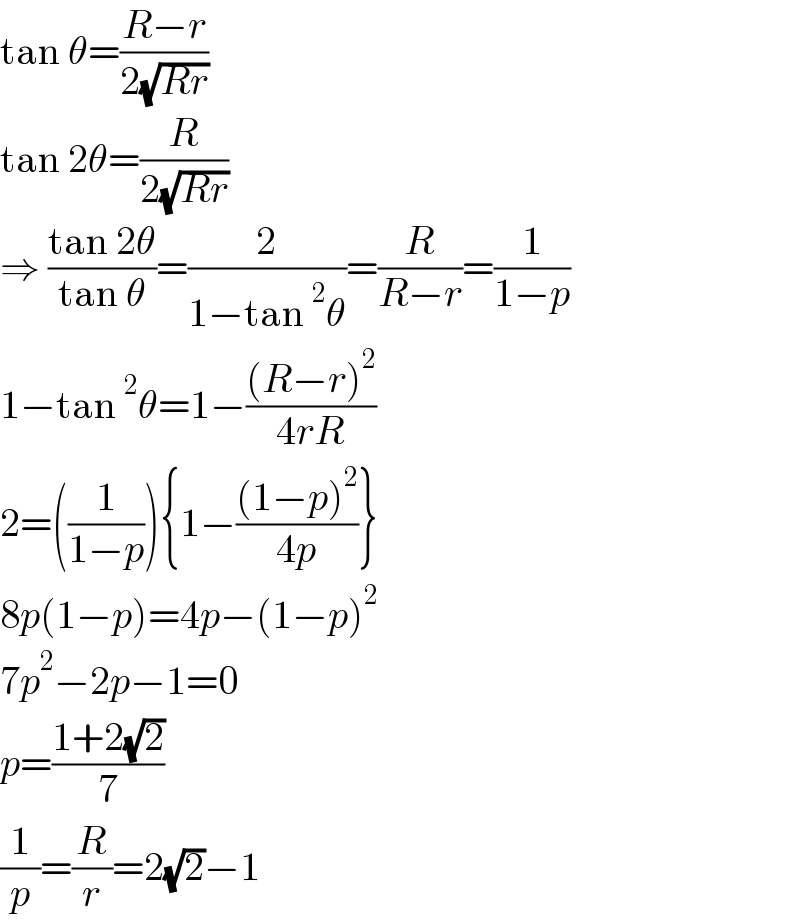
tan θ=((R−r)/(2(√(Rr)))) tan 2θ=(R/(2(√(Rr)))) ⇒ ((tan 2θ)/(tan θ))=(2/(1−tan^2 θ))=(R/(R−r))=(1/(1−p)) 1−tan^2 θ=1−(((R−r)^2 )/(4rR)) 2=((1/(1−p))){1−(((1−p)^2 )/(4p))} 8p(1−p)=4p−(1−p)^2 7p^2 −2p−1=0 p=((1+2(√2))/7) (1/p)=(R/r)=2(√2)−1

$$\mathrm{tan}\:\theta=\frac{{R}−{r}}{\mathrm{2}\sqrt{{Rr}}} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=\frac{{R}}{\mathrm{2}\sqrt{{Rr}}} \\ $$$$\Rightarrow\:\frac{\mathrm{tan}\:\mathrm{2}\theta}{\mathrm{tan}\:\theta}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta}=\frac{{R}}{{R}−{r}}=\frac{\mathrm{1}}{\mathrm{1}−{p}} \\ $$$$\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta=\mathrm{1}−\frac{\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{rR}} \\ $$$$\mathrm{2}=\left(\frac{\mathrm{1}}{\mathrm{1}−{p}}\right)\left\{\mathrm{1}−\frac{\left(\mathrm{1}−{p}\right)^{\mathrm{2}} }{\mathrm{4}{p}}\right\} \\ $$$$\mathrm{8}{p}\left(\mathrm{1}−{p}\right)=\mathrm{4}{p}−\left(\mathrm{1}−{p}\right)^{\mathrm{2}} \\ $$$$\mathrm{7}{p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{1}=\mathrm{0} \\ $$$${p}=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{7}} \\ $$$$\frac{\mathrm{1}}{{p}}=\frac{{R}}{{r}}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1} \\ $$

Answered by MathematicalUser2357 last updated on 12/Dec/24

Oh this might be it

$$\mathrm{Oh}\:\mathrm{this}\:\mathrm{might}\:\mathrm{be}\:\mathrm{it} \\ $$$$ \\ $$

Commented by mr W last updated on 12/Dec/24

this app is powerful for writting formulae, but weak for drawing diagrams.

$${this}\:{app}\:{is}\:{powerful}\:{for}\:{writting} \\ $$$${formulae},\:{but}\:{weak}\:{for}\:{drawing} \\ $$$${diagrams}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com