Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 214372 by ajfour last updated on 06/Dec/24

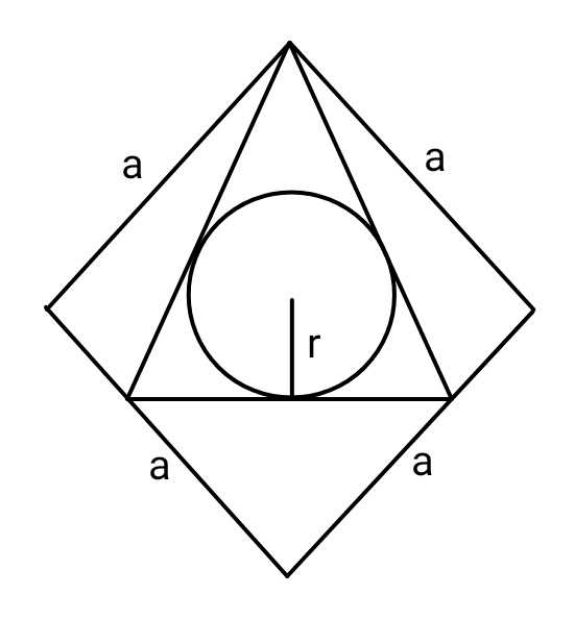
Commented by ajfour last updated on 06/Dec/24

Find maximum r. Outer figure is a rhombus.Circle is inscribed in an isosceles triangle as shown above.

$${Find}\:{maximum}\:{r}.\:{Outer}\:{figure}\:{is}\:{a} \\ $$$${rhombus}.{Circle}\:{is}\:{inscribed}\:{in}\:{an}\: \\ $$$${isosceles}\:{triangle}\:{as}\:{shown}\:{above}. \\ $$

Answered by a.lgnaoui last updated on 07/Dec/24

on peut verifier facilement que le rayon r est maximum lorsqaue y=x=45° alors AB=(a/2) tan 45=(r/(a/2))=((2r)/a) alors r=(a/2)

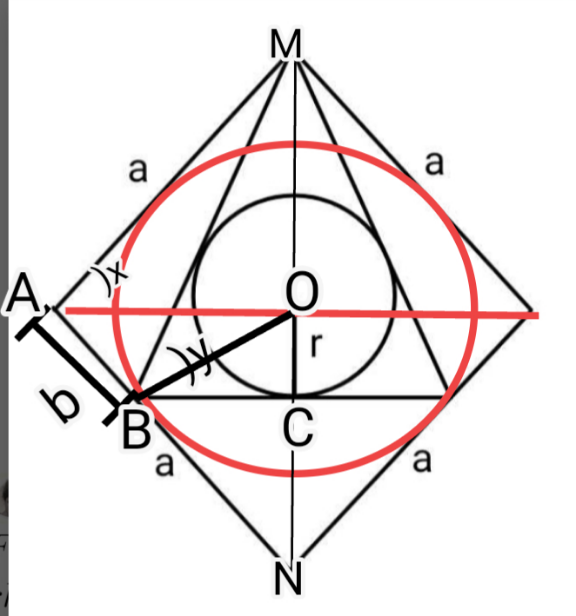
$$\mathrm{on}\:\mathrm{peut}\:\mathrm{verifier}\:\:\mathrm{facilement}\:\mathrm{que}\:\mathrm{le}\:\mathrm{rayon}\:\boldsymbol{\mathrm{r}}\:\boldsymbol{\mathrm{est}}\: \\ $$$$\boldsymbol{\mathrm{maximum}}\:\mathrm{lorsqaue}\:\:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{x}}=\mathrm{45}° \\ $$$$\mathrm{alors}\:\:\mathrm{AB}=\frac{\mathrm{a}}{\mathrm{2}}\:\:\:\mathrm{tan}\:\mathrm{45}=\frac{\boldsymbol{\mathrm{r}}}{\boldsymbol{\mathrm{a}}/\mathrm{2}}=\frac{\mathrm{2}\boldsymbol{\mathrm{r}}}{\boldsymbol{\mathrm{a}}} \\ $$$$\boldsymbol{\mathrm{alors}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{r}}=\frac{\boldsymbol{\mathrm{a}}}{\mathrm{2}} \\ $$$$\:\: \\ $$

Commented by a.lgnaoui last updated on 07/Dec/24

Commented by mr W last updated on 07/Dec/24

non−sense again. the circle should be inscribed in the isosceles triangle, not in the rhombus!

$${non}−{sense}\:{again}.\:{the}\:{circle}\:{should} \\ $$$${be}\:{inscribed}\:{in}\:{the}\:{isosceles}\: \\ $$$${triangle},\:{not}\:{in}\:{the}\:{rhombus}! \\ $$

Answered by mr W last updated on 07/Dec/24

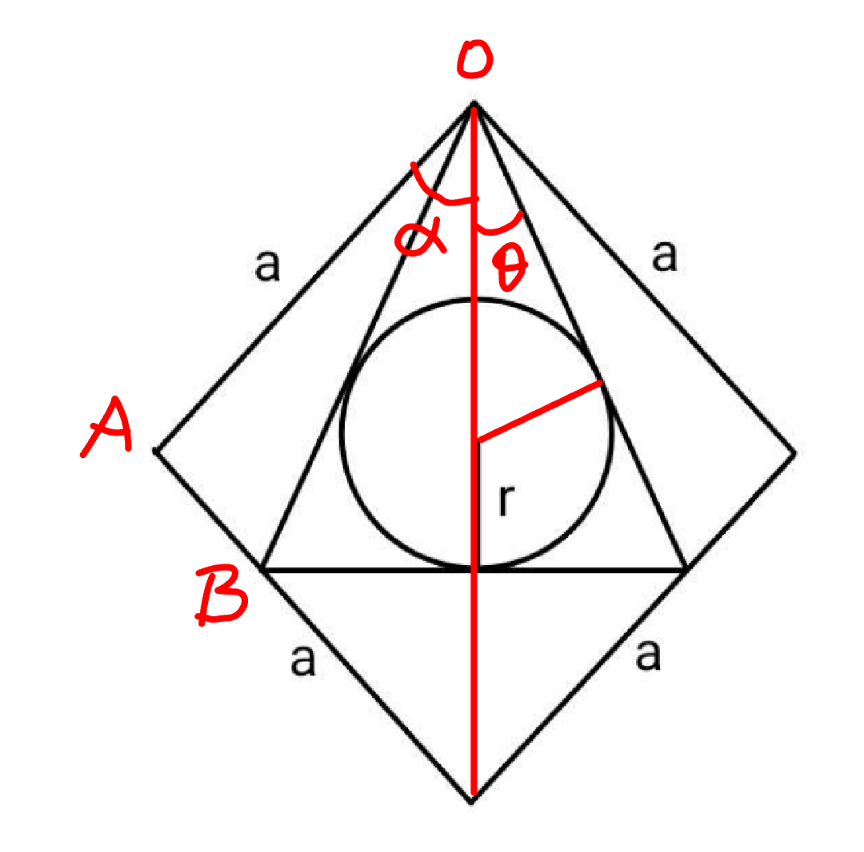
Commented by mr W last updated on 07/Dec/24

0<θ≤α<(π/2) OB=((r+(r/(sin θ)))/(cos θ))=(((1+sin θ)r)/(sin θ cos θ)) ((OB)/(sin (π−2α)))=(a/(sin (π−2α+α−θ))) (((1+sin θ)r)/(sin θ cos θ sin 2α))=(a/(sin (θ+α)))=(a/(sin θ cos α+cos θ sin α)) ⇒(r/(2a))=((sin θ sin α)/((1+sin θ)(tan θ+ tan α))) Φ=ln ((r/(2a)))=ln (sin θ)+ln (sin α)−ln (1+sin θ)−ln (tan θ+tan α) r_(max) ⇔ Φ_(max) (∂Φ/∂α)=(1/(tan α))−(1/((tan θ+tan α)cos^2 α))=0 tan θ=((1/(cos^2 α))−1)tan α=tan^3 α ⇒tan α=((tan θ))^(1/3) (∂Φ/∂θ)=(1/(tan θ))−((cos θ)/(1+sin θ))−(1/((tan θ+tan α)cos^2 θ))=0 ((1/(tan θ))−((cos θ)/(1+sin θ)))cos^2 θ=(1/(tan θ+tan α)) ⇒cos^2 θ((1/(tan θ))−((cos θ)/(1+sin θ)))=(1/(tan θ+((tan θ))^(1/3) )) ⇒θ≈0.5984 (34.286°) ⇒α≈0.7218 (41.356°) ≠45° ⇒(r_(max) /a)≈0.304840051439 ✓ example with a=4 see below

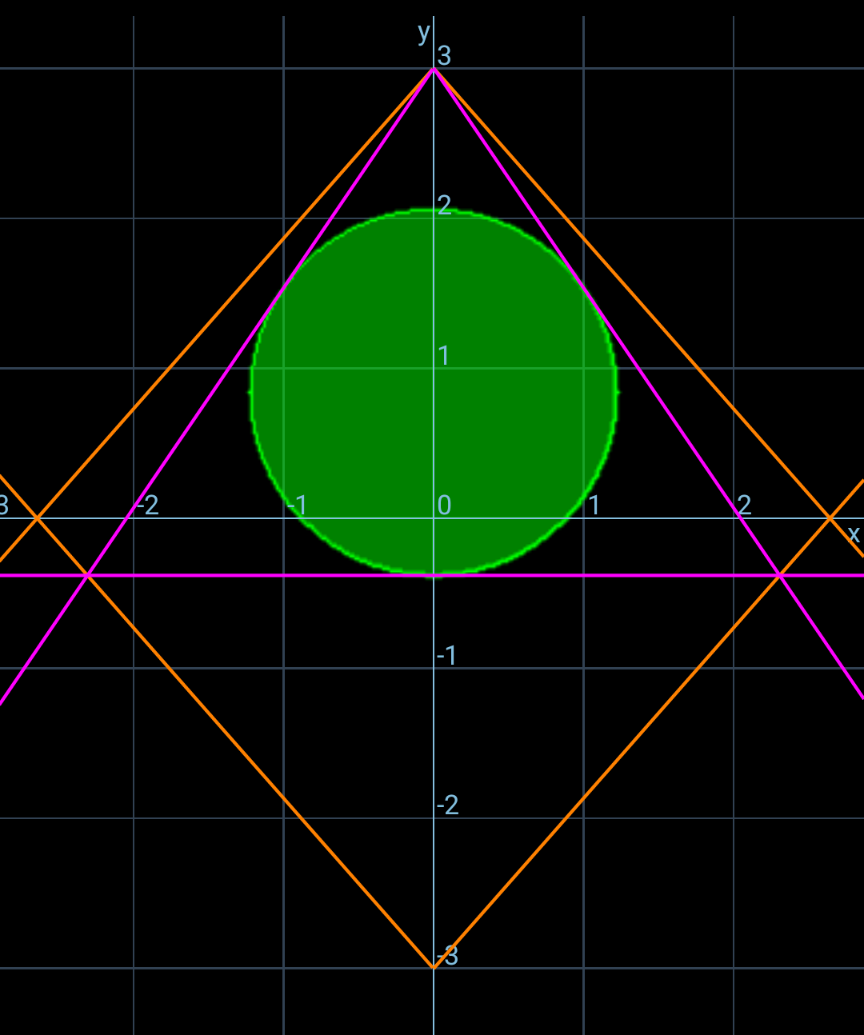
$$\mathrm{0}<\theta\leqslant\alpha<\frac{\pi}{\mathrm{2}} \\ $$$${OB}=\frac{{r}+\frac{{r}}{\mathrm{sin}\:\theta}}{\mathrm{cos}\:\theta}=\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right){r}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$\frac{{OB}}{\mathrm{sin}\:\left(\pi−\mathrm{2}\alpha\right)}=\frac{{a}}{\mathrm{sin}\:\left(\pi−\mathrm{2}\alpha+\alpha−\theta\right)} \\ $$$$\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right){r}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\alpha}=\frac{{a}}{\mathrm{sin}\:\left(\theta+\alpha\right)}=\frac{{a}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow\frac{{r}}{\mathrm{2}{a}}=\frac{\mathrm{sin}\:\theta\:\mathrm{sin}\:\alpha}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{tan}\:\theta+\:\mathrm{tan}\:\alpha\right)} \\ $$$$\Phi=\mathrm{ln}\:\left(\frac{{r}}{\mathrm{2}{a}}\right)=\mathrm{ln}\:\left(\mathrm{sin}\:\theta\right)+\mathrm{ln}\:\left(\mathrm{sin}\:\alpha\right)−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:\theta\right)−\mathrm{ln}\:\left(\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha\right) \\ $$$${r}_{{max}} \:\Leftrightarrow\:\Phi_{{max}} \\ $$$$\frac{\partial\Phi}{\partial\alpha}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\mathrm{1}}{\left(\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha\right)\mathrm{cos}^{\mathrm{2}} \:\alpha}=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta=\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\alpha}−\mathrm{1}\right)\mathrm{tan}\:\alpha=\mathrm{tan}^{\mathrm{3}} \:\alpha \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\sqrt[{\mathrm{3}}]{\mathrm{tan}\:\theta} \\ $$$$\frac{\partial\Phi}{\partial\theta}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}−\frac{\mathrm{1}}{\left(\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha\right)\mathrm{cos}^{\mathrm{2}} \:\theta}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right)\mathrm{cos}^{\mathrm{2}} \:\theta=\frac{\mathrm{1}}{\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\theta\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\theta+\sqrt[{\mathrm{3}}]{\mathrm{tan}\:\theta}} \\ $$$$\Rightarrow\theta\approx\mathrm{0}.\mathrm{5984}\:\left(\mathrm{34}.\mathrm{286}°\right) \\ $$$$\Rightarrow\alpha\approx\mathrm{0}.\mathrm{7218}\:\left(\mathrm{41}.\mathrm{356}°\right)\:\neq\mathrm{45}° \\ $$$$\Rightarrow\frac{{r}_{{max}} }{{a}}\approx\mathrm{0}.\mathrm{304840051439}\:\checkmark \\ $$$${example}\:{with}\:{a}=\mathrm{4}\:{see}\:{below} \\ $$

Commented by mr W last updated on 07/Dec/24

Commented by ajfour last updated on 08/Dec/24

Thanks for your solution. I am trying still sometimes..

$${Thanks}\:{for}\:{your}\:{solution}.\:{I}\:{am} \\ $$$${trying}\:{still}\:{sometimes}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com