
Question Number 214297 by ajfour last updated on 04/Dec/24
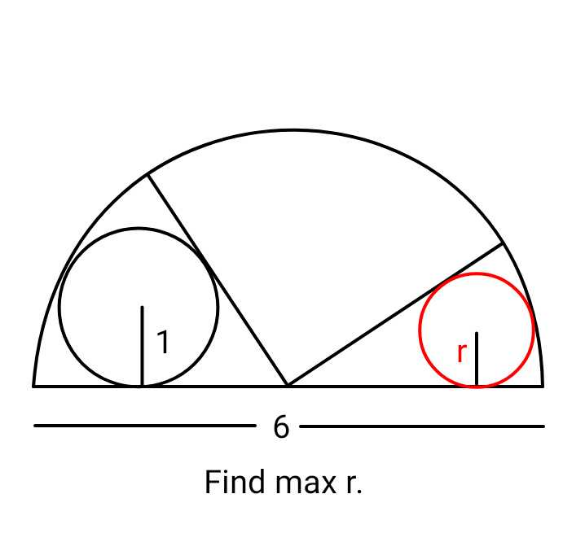
Commented by ajfour last updated on 04/Dec/24
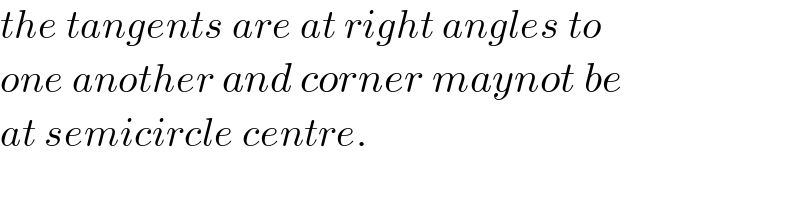
$${the}\:{tangents}\:{are}\:{at}\:{right}\:{angles}\:{to} \\ $$$${one}\:{another}\:{and}\:{corner}\:{maynot}\:{be} \\ $$$${at}\:{semicircle}\:{centre}. \\ $$
Commented by mr W last updated on 05/Dec/24
��
Commented by ajfour last updated on 05/Dec/24
https://youtu.be/ys6xN29xNUM?si=9rk6nXD0GcmHTp9Z
Answered by mr W last updated on 04/Dec/24
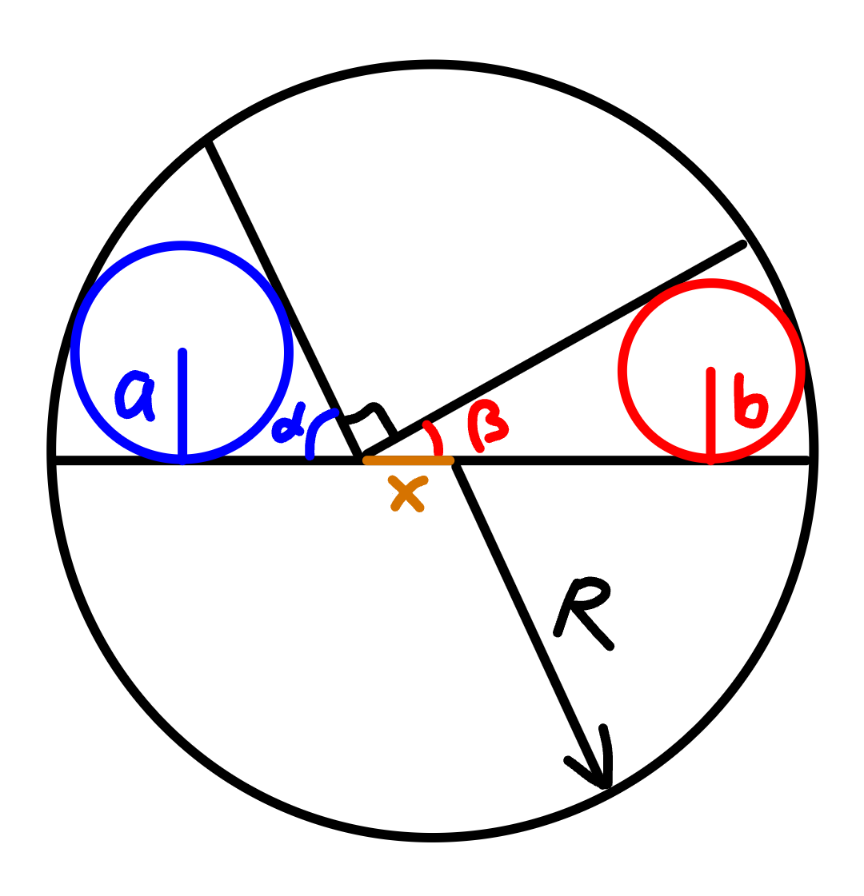
Commented by mr W last updated on 06/Dec/24
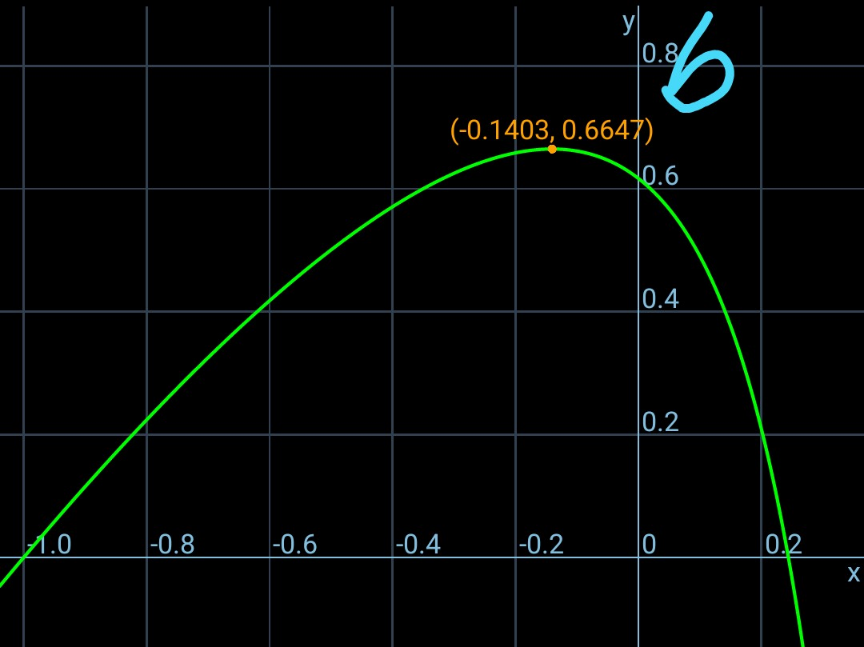
![a=1 R=3 b=r (b/(tan (β/2)))=x+(√((R−b)^2 −b^2 ))=x+(√(R^2 −2Rb)) ⇒tan (β/2)=(b/(x+(√(R^2 −2Rb)))) similarly ⇒tan (α/2)=(a/(−x+(√(R^2 −2Ra)))) (β/2)=(π/4)−(α/2) tan (β/2)=((1−tan (a/2))/(1+tan (a/2))) (b/(x+(√(R^2 −2Rb))))=((1−(a/(−x+(√(R^2 −2Ra)))))/(1+(a/(−x+(√(R^2 −2Ra)))))) (b/(x+(√(R^2 −2Rb))))=((−x+(√(R^2 −2Ra))−a)/(−x+(√(R^2 −2Ra))+a)) let α=(a/R), β=(b/R), ξ=(x/R) (β/(ξ+(√(1−2β))))=((−ξ+(√(1−2α))−α)/(−ξ+(√(1−2α))+α)) let λ=(√(1−2β)), p=(√(1−2α))+α, q=(√(1−2α))−α ((1−λ^2 )/(2(ξ+λ)))=((q−ξ)/(p−ξ)) (p−ξ)λ^2 +2(q−ξ)λ+(2q+1)ξ−[2ξ^2 −(2q+1)ξ+p]=0 λ=((ξ−q+(√((ξ−q)^2 +(p−ξ)[2ξ^2 −(2q+1)ξ+p])))/(p−ξ)) b={1−{((ξ−q+(√((ξ−q)^2 +(p−ξ)[2ξ^2 −(2q+1)ξ+p])))/(p−ξ))}^2 }(R/2) b_(max) ≈0.66471561 at ξ=(x/R)≈−0.14031961 =================](Q214305.png)
$${a}=\mathrm{1} \\ $$$${R}=\mathrm{3} \\ $$$${b}={r} \\ $$$$\frac{{b}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}={x}+\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }={x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{{b}}{{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}}} \\ $$$${similarly} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{{a}}{−{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Ra}}} \\ $$$$\frac{\beta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{tan}\:\frac{{a}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{{a}}{\mathrm{2}}} \\ $$$$\frac{{b}}{{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}}}=\frac{\mathrm{1}−\frac{{a}}{−{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Ra}}}}{\mathrm{1}+\frac{{a}}{−{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Ra}}}} \\ $$$$\frac{{b}}{{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rb}}}=\frac{−{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Ra}}−{a}}{−{x}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Ra}}+{a}} \\ $$$${let}\:\alpha=\frac{{a}}{{R}},\:\beta=\frac{{b}}{{R}},\:\xi=\frac{{x}}{{R}} \\ $$$$\frac{\beta}{\xi+\sqrt{\mathrm{1}−\mathrm{2}\beta}}=\frac{−\xi+\sqrt{\mathrm{1}−\mathrm{2}\alpha}−\alpha}{−\xi+\sqrt{\mathrm{1}−\mathrm{2}\alpha}+\alpha} \\ $$$${let}\:\lambda=\sqrt{\mathrm{1}−\mathrm{2}\beta},\:{p}=\sqrt{\mathrm{1}−\mathrm{2}\alpha}+\alpha,\:{q}=\sqrt{\mathrm{1}−\mathrm{2}\alpha}−\alpha \\ $$$$\frac{\mathrm{1}−\lambda^{\mathrm{2}} }{\mathrm{2}\left(\xi+\lambda\right)}=\frac{{q}−\xi}{{p}−\xi} \\ $$$$\left({p}−\xi\right)\lambda^{\mathrm{2}} +\mathrm{2}\left({q}−\xi\right)\lambda+\left(\mathrm{2}{q}+\mathrm{1}\right)\xi−\left[\mathrm{2}\xi^{\mathrm{2}} −\left(\mathrm{2}{q}+\mathrm{1}\right)\xi+{p}\right]=\mathrm{0} \\ $$$$\lambda=\frac{\xi−{q}+\sqrt{\left(\xi−{q}\right)^{\mathrm{2}} +\left({p}−\xi\right)\left[\mathrm{2}\xi^{\mathrm{2}} −\left(\mathrm{2}{q}+\mathrm{1}\right)\xi+{p}\right]}}{{p}−\xi} \\ $$$${b}=\left\{\mathrm{1}−\left\{\frac{\xi−{q}+\sqrt{\left(\xi−{q}\right)^{\mathrm{2}} +\left({p}−\xi\right)\left[\mathrm{2}\xi^{\mathrm{2}} −\left(\mathrm{2}{q}+\mathrm{1}\right)\xi+{p}\right]}}{{p}−\xi}\right\}^{\mathrm{2}} \right\}\frac{{R}}{\mathrm{2}} \\ $$$${b}_{{max}} \approx\mathrm{0}.\mathrm{66471561}\:{at}\:\xi=\frac{{x}}{{R}}\approx−\mathrm{0}.\mathrm{14031961} \\ $$$$================= \\ $$
Commented by mr W last updated on 06/Dec/24
Commented by ajfour last updated on 06/Dec/24
![(a/(R−a))=sin θ (R−a)cos θ=acot (α/2)+x R+x=bcot (β/2) (α/2)+(β/2)=(π/4) ((A+B)/(1−AB))=1 [ for ((tan (α/2)+tan (β/2))/(1−tan (α/2)tan (β/2)))=1] A+B=1−AB (a/((R−a)cos θ−x))+(b/(R+x)) +((ab)/((R+x){(R−a)cos θ−x}))=1 or a(R+x)+b(R−a)cos θ−bx+ab +x^2 +{R−(R−a)cos θ}x−R(R−a)cos θ=0 or x^2 +{a−b+R−(R−a)cos θ}x+a(b+R) +(b−R)(R−a)cos θ=0 diff. 2x+{a−b+R−(R−a)cos θ}=0 or (R−a)cos θ−x=R+x+a−b x=((b−a−R+(R−a)cos θ)/2) b{(1/(R+x))+(a/((R+x){(R−a)cos θ−x))} =1−(a/({(R−a)cos θ−x}))](Q214358.png)
$$\frac{{a}}{{R}−{a}}=\mathrm{sin}\:\theta \\ $$$$\left({R}−{a}\right)\mathrm{cos}\:\theta={a}\mathrm{cot}\:\frac{\alpha}{\mathrm{2}}+{x} \\ $$$${R}+{x}={b}\mathrm{cot}\:\frac{\beta}{\mathrm{2}} \\ $$$$\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$\frac{{A}+{B}}{\mathrm{1}−{AB}}=\mathrm{1}\:\:\:\left[\:\:{for}\:\:\frac{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}+\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}=\mathrm{1}\right] \\ $$$${A}+{B}=\mathrm{1}−{AB} \\ $$$$\frac{{a}}{\left({R}−{a}\right)\mathrm{cos}\:\theta−{x}}+\frac{{b}}{{R}+{x}} \\ $$$$\:\:\:\:\:\:\:+\frac{{ab}}{\left({R}+{x}\right)\left\{\left({R}−{a}\right)\mathrm{cos}\:\theta−{x}\right\}}=\mathrm{1} \\ $$$${or} \\ $$$${a}\left({R}+{x}\right)+{b}\left({R}−{a}\right)\mathrm{cos}\:\theta−{bx}+{ab} \\ $$$$\:\:+{x}^{\mathrm{2}} +\left\{{R}−\left({R}−{a}\right)\mathrm{cos}\:\theta\right\}{x}−{R}\left({R}−{a}\right)\mathrm{cos}\:\theta=\mathrm{0} \\ $$$${or} \\ $$$${x}^{\mathrm{2}} +\left\{{a}−{b}+{R}−\left({R}−{a}\right)\mathrm{cos}\:\theta\right\}{x}+{a}\left({b}+{R}\right) \\ $$$$\:\:\:\:\:\:\:+\left({b}−{R}\right)\left({R}−{a}\right)\mathrm{cos}\:\theta=\mathrm{0} \\ $$$${diff}. \\ $$$$\mathrm{2}{x}+\left\{{a}−{b}+{R}−\left({R}−{a}\right)\mathrm{cos}\:\theta\right\}=\mathrm{0} \\ $$$${or}\:\left({R}−{a}\right)\mathrm{cos}\:\theta−{x}={R}+{x}+{a}−{b} \\ $$$${x}=\frac{{b}−{a}−{R}+\left({R}−{a}\right)\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$${b}\left\{\frac{\mathrm{1}}{{R}+{x}}+\frac{{a}}{\left({R}+{x}\right)\left\{\left({R}−{a}\right)\mathrm{cos}\:\theta−{x}\right.}\right\} \\ $$$$\:\:\:=\mathrm{1}−\frac{{a}}{\left\{\left({R}−{a}\right)\mathrm{cos}\:\theta−{x}\right\}} \\ $$
