
Question Number 214163 by deleted31 last updated on 29/Nov/24
Commented by mathkun last updated on 30/Nov/24

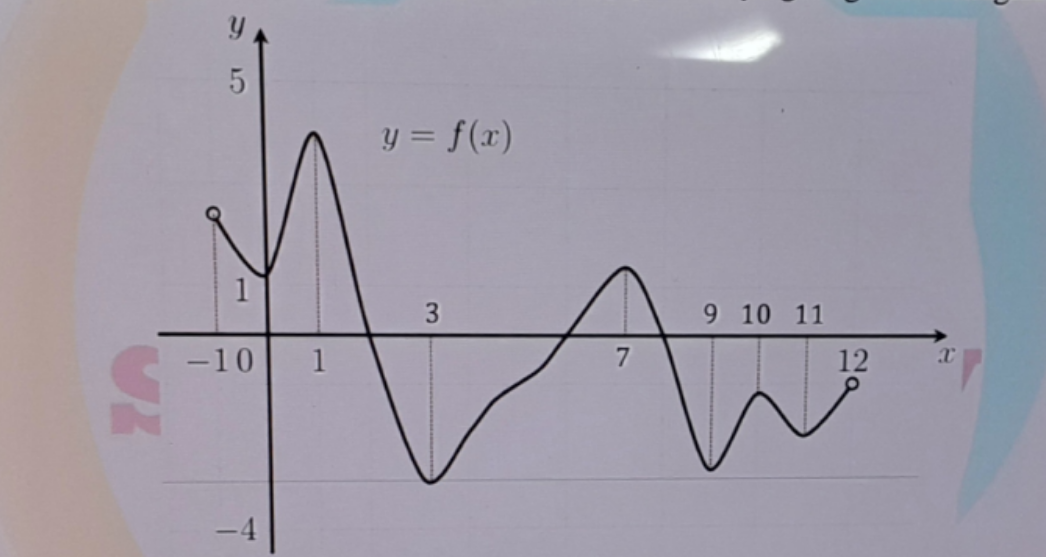
$$\mathrm{I}\:\mathrm{am}\:\mathrm{a}\:\mathrm{begginer}\:\mathrm{in}\:\mathrm{Calculus}. \\ $$$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function}? \\ $$$$\mathrm{The}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{y}\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{given}. \\ $$
Commented by deleted31 last updated on 30/Nov/24

$$\left.\::\right) \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{nonsense}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{derivative} \\ $$$$\mathrm{of}\:\mathrm{that}\:\mathrm{function}\:\frac{\mathrm{d}{y}\left({t}\right)}{\mathrm{d}{t}}\:\mathrm{Because}\: \\ $$$$\mathrm{function}\:{y}\left({t}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{clearly}\:\mathrm{specified} \\ $$$$\mathrm{however}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\: \\ $$$$\frac{\mathrm{d}{y}\left({t}\right)}{\mathrm{d}{t}}=\mathrm{0}\:\:\mathrm{the}\:\mathrm{meaning}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{differantial}\:\mathrm{coefficient}\:\mathrm{0}\:\mathrm{is}\:\mathrm{because} \\ $$$$\mathrm{it}\:\mathrm{can}\:\mathrm{regarded}\:\mathrm{as}\:\mathrm{the}\:\mathrm{maximum}/\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{function}\:\mathrm{pls}\:\mathrm{find}\:\mathrm{wikipedia} \\ $$$$\mathrm{documents}\:\mathrm{Maximum}\:\mathrm{and}\:\mathrm{Minimum} \\ $$
Commented by deleted31 last updated on 30/Nov/24

$$\mathrm{and}\:\mathrm{Quiz}\:\mathrm{i}'\mathrm{ve}\:\mathrm{created}\:\mathrm{is}\:\mathrm{about} \\ $$$$\mathrm{inflection}\:\mathrm{point}\:\mathrm{which}\:\mathrm{are}\:\mathrm{also}\:\mathrm{where} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{the}\:\mathrm{point}\:\mathrm{where}\:\mathrm{the} \\ $$$$\mathrm{Shape}\:\mathrm{of}\:\mathrm{a}\:\mathrm{function}\:\mathrm{change}\:\mathrm{from}\:\mathrm{a} \\ $$$$\mathrm{concave}\:\mathrm{function}\:\mathrm{to}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{function} \\ $$$$\mathrm{without}\:\mathrm{having}\:\mathrm{to}\:\mathrm{differantial}\:\mathrm{twice} \\ $$
Answered by deleted31 last updated on 29/Nov/24

$$\mathrm{additional}\:\mathrm{problem}! \\ $$$${f};\mathbb{R}^{\mathrm{1}} \rightarrow\mathbb{R}^{\mathrm{1}} \:,\:{f}\in\boldsymbol{\mathcal{C}}^{{n}} \:\mathrm{at}\:{t}\in\left(−\infty,\infty\right)\: \\ $$$$\left({f}\:\mathrm{is}\:{n}\:\mathrm{time}\:\mathrm{differantiable}\:\mathrm{function}\right) \\ $$$$\mathrm{find}\:\mathrm{inflection}\:\mathrm{point}\:\mathrm{of}\:\:{f}\left({t}\right) \\ $$$$\mathrm{where}\:\mathrm{intervel}\:{t}\in\left(\mathrm{0},\infty\right)\: \\ $$$$\left.\mathrm{Do}\:\mathrm{you}\:\mathrm{want}\:\mathrm{try}\:\mathrm{it}??\::\right) \\ $$
