Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 214138 by abdelsalam last updated on 29/Nov/24

Commented by abdelsalam last updated on 29/Nov/24

find x

$${find}\:\:{x} \\ $$

Answered by issac last updated on 29/Nov/24

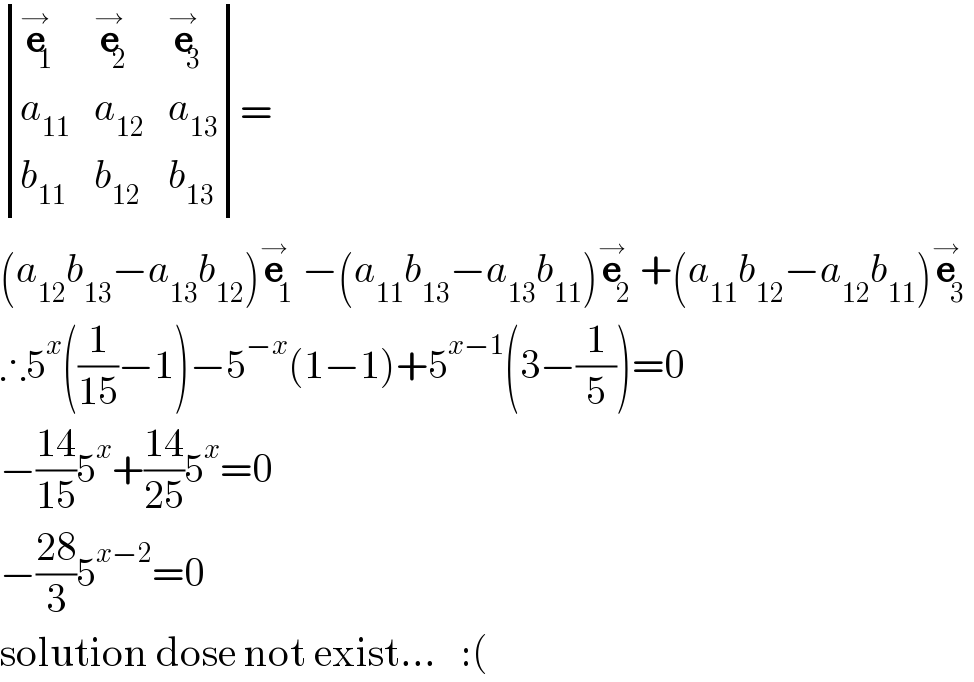
determinant ((e_1 ^→ ,e_2 ^→ ,e_3 ^→ ),(a_(11) ,a_(12) ,a_(13) ),(b_(11) ,b_(12) ,b_(13) ))= (a_(12) b_(13) −a_(13) b_(12) )e_1 ^→ −(a_(11) b_(13) −a_(13) b_(11) )e_2 ^→ +(a_(11) b_(12) −a_(12) b_(11) )e_3 ^→ ∴5^x ((1/(15))−1)−5^(−x) (1−1)+5^(x−1) (3−(1/5))=0 −((14)/(15))5^x +((14)/(25))5^x =0 −((28)/3)5^(x−2) =0 solution dose not exist... :(

$$\begin{vmatrix}{\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{1}} }&{\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{2}} }&{\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{3}} }\\{{a}_{\mathrm{11}} }&{{a}_{\mathrm{12}} }&{{a}_{\mathrm{13}} }\\{{b}_{\mathrm{11}} }&{{b}_{\mathrm{12}} }&{{b}_{\mathrm{13}} }\end{vmatrix}= \\ $$$$\left({a}_{\mathrm{12}} {b}_{\mathrm{13}} −{a}_{\mathrm{13}} {b}_{\mathrm{12}} \right)\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{1}} −\left({a}_{\mathrm{11}} {b}_{\mathrm{13}} −{a}_{\mathrm{13}} {b}_{\mathrm{11}} \right)\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{2}} +\left({a}_{\mathrm{11}} {b}_{\mathrm{12}} −{a}_{\mathrm{12}} {b}_{\mathrm{11}} \right)\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{3}} \\ $$$$\therefore\mathrm{5}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{15}}−\mathrm{1}\right)−\mathrm{5}^{−{x}} \left(\mathrm{1}−\mathrm{1}\right)+\mathrm{5}^{{x}−\mathrm{1}} \left(\mathrm{3}−\frac{\mathrm{1}}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$−\frac{\mathrm{14}}{\mathrm{15}}\mathrm{5}^{{x}} +\frac{\mathrm{14}}{\mathrm{25}}\mathrm{5}^{{x}} =\mathrm{0} \\ $$$$−\frac{\mathrm{28}}{\mathrm{3}}\mathrm{5}^{{x}−\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{solution}\:\mathrm{dose}\:\mathrm{not}\:\mathrm{exist}...\:\:\::\left(\right. \\ $$

Commented by abdelsalam last updated on 29/Nov/24

Thanks

$${Thanks} \\ $$

Answered by Rasheed.Sindhi last updated on 29/Nov/24

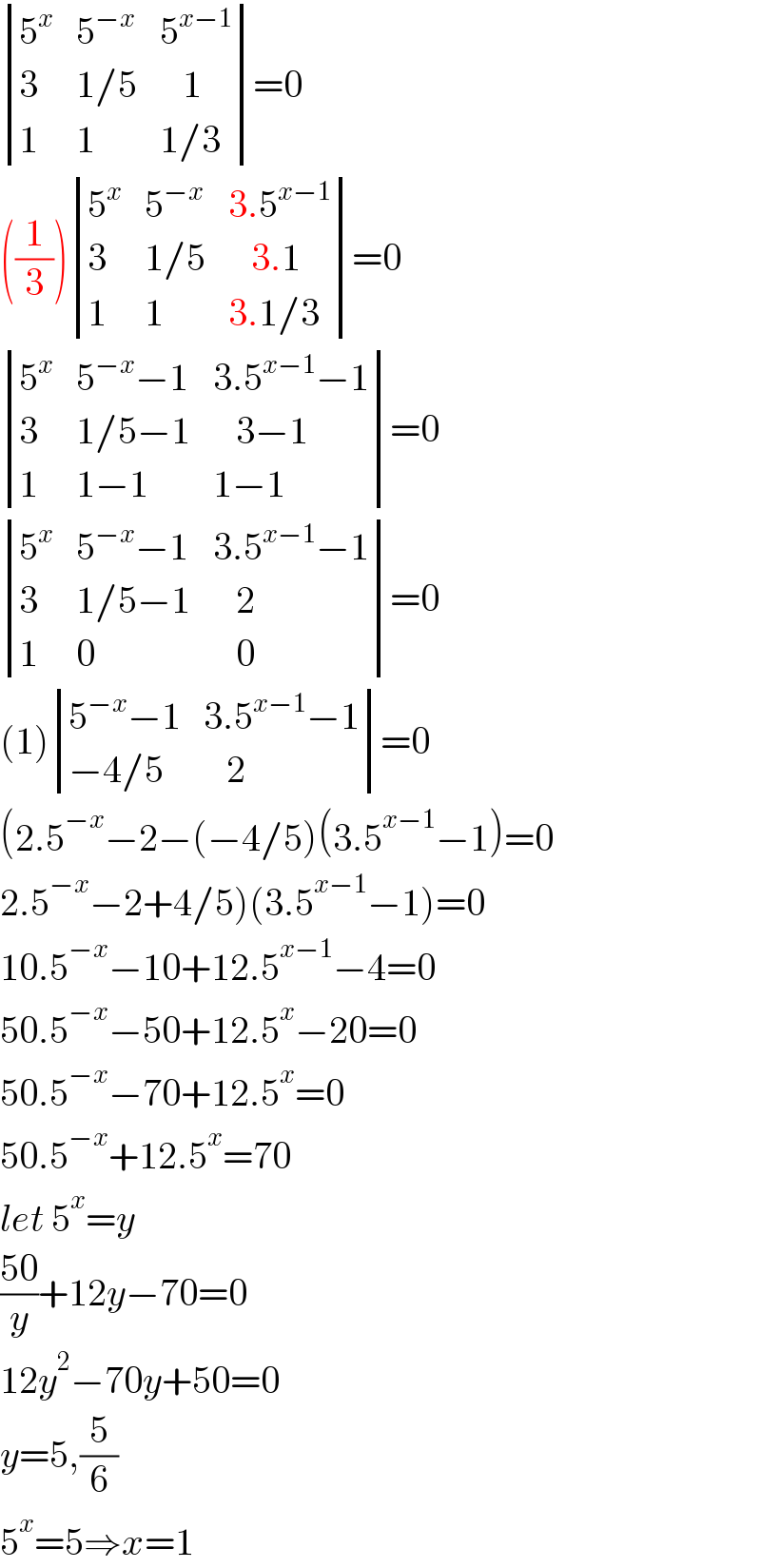
determinant ((5^x ,5^(−x) ,5^(x−1) ),(3,(1/5),( 1)),(1,1,(1/3)))=0 ((1/3)) determinant ((5^x ,5^(−x) ,(3.5^(x−1) )),(3,(1/5),( 3.1)),(1,1,(3.1/3)))=0 determinant ((5^x ,(5^(−x) −1),(3.5^(x−1) −1)),(3,(1/5−1),( 3−1)),(1,(1−1),(1−1)))=0 determinant ((5^x ,(5^(−x) −1),(3.5^(x−1) −1)),(3,(1/5−1),( 2)),(1,0,( 0)))=0 (1) determinant (((5^(−x) −1),(3.5^(x−1) −1)),((−4/5),( 2)))=0 (2.5^(−x) −2−(−4/5)(3.5^(x−1) −1)=0 2.5^(−x) −2+4/5)(3.5^(x−1) −1)=0 10.5^(−x) −10+12.5^(x−1) −4=0 50.5^(−x) −50+12.5^x −20=0 50.5^(−x) −70+12.5^x =0 50.5^(−x) +12.5^x =70 let 5^x =y ((50)/y)+12y−70=0 12y^2 −70y+50=0 y=5,(5/6) 5^x =5⇒x=1

$$\begin{vmatrix}{\mathrm{5}^{{x}} }&{\mathrm{5}^{−{x}} }&{\mathrm{5}^{{x}−\mathrm{1}} }\\{\mathrm{3}}&{\mathrm{1}/\mathrm{5}}&{\:\:\:\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{3}}\end{vmatrix}=\mathrm{0}\: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\begin{vmatrix}{\mathrm{5}^{{x}} }&{\mathrm{5}^{−{x}} }&{\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} }\\{\mathrm{3}}&{\mathrm{1}/\mathrm{5}}&{\:\:\:\mathrm{3}.\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{3}.\mathrm{1}/\mathrm{3}}\end{vmatrix}=\mathrm{0}\: \\ $$$$\begin{vmatrix}{\mathrm{5}^{{x}} }&{\mathrm{5}^{−{x}} −\mathrm{1}}&{\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{1}}\\{\mathrm{3}}&{\mathrm{1}/\mathrm{5}−\mathrm{1}}&{\:\:\:\mathrm{3}−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}−\mathrm{1}}&{\mathrm{1}−\mathrm{1}}\end{vmatrix}=\mathrm{0}\:\: \\ $$$$\begin{vmatrix}{\mathrm{5}^{{x}} }&{\mathrm{5}^{−{x}} −\mathrm{1}}&{\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{1}}\\{\mathrm{3}}&{\mathrm{1}/\mathrm{5}−\mathrm{1}}&{\:\:\:\mathrm{2}}\\{\mathrm{1}}&{\mathrm{0}}&{\:\:\:\mathrm{0}}\end{vmatrix}=\mathrm{0}\:\: \\ $$$$\left(\mathrm{1}\right)\begin{vmatrix}{\mathrm{5}^{−{x}} −\mathrm{1}}&{\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{1}}\\{−\mathrm{4}/\mathrm{5}}&{\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{0} \\ $$$$\left(\mathrm{2}.\mathrm{5}^{−{x}} −\mathrm{2}−\left(−\mathrm{4}/\mathrm{5}\right)\left(\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{0}\right. \\ $$$$\left.\mathrm{2}.\mathrm{5}^{−{x}} −\mathrm{2}+\mathrm{4}/\mathrm{5}\right)\left(\mathrm{3}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{10}.\mathrm{5}^{−{x}} −\mathrm{10}+\mathrm{12}.\mathrm{5}^{{x}−\mathrm{1}} −\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{50}.\mathrm{5}^{−{x}} −\mathrm{50}+\mathrm{12}.\mathrm{5}^{{x}} −\mathrm{20}=\mathrm{0} \\ $$$$\mathrm{50}.\mathrm{5}^{−{x}} −\mathrm{70}+\mathrm{12}.\mathrm{5}^{{x}} =\mathrm{0} \\ $$$$\mathrm{50}.\mathrm{5}^{−{x}} +\mathrm{12}.\mathrm{5}^{{x}} =\mathrm{70} \\ $$$${let}\:\mathrm{5}^{{x}} ={y} \\ $$$$\frac{\mathrm{50}}{{y}}+\mathrm{12}{y}−\mathrm{70}=\mathrm{0} \\ $$$$\mathrm{12}{y}^{\mathrm{2}} −\mathrm{70}{y}+\mathrm{50}=\mathrm{0} \\ $$$${y}=\mathrm{5},\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{5}^{{x}} =\mathrm{5}\Rightarrow{x}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com