Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 214132 by ajfour last updated on 29/Nov/24

Answered by MathematicalUser2357 last updated on 29/Nov/24

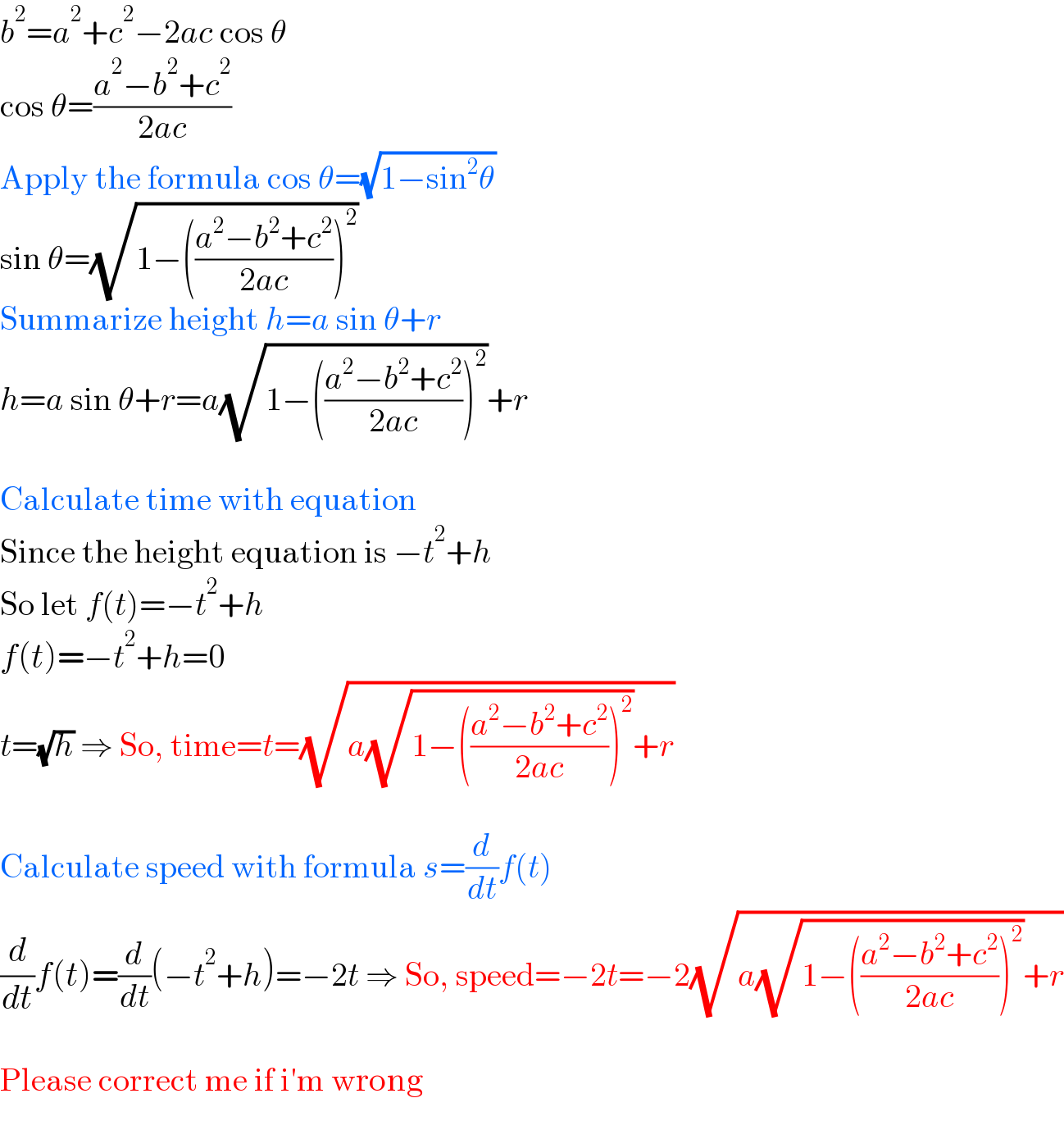
b^2 =a^2 +c^2 −2ac cos θ cos θ=((a^2 −b^2 +c^2 )/(2ac)) Apply the formula cos θ=(√(1−sin^2 θ)) sin θ=(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 )) Summarize height h=a sin θ+r h=a sin θ+r=a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r Calculate time with equation Since the height equation is −t^2 +h So let f(t)=−t^2 +h f(t)=−t^2 +h=0 t=(√h) ⇒ So, time=t=(√(a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r)) Calculate speed with formula s=(d/dt)f(t) (d/dt)f(t)=(d/dt)(−t^2 +h)=−2t ⇒ So, speed=−2t=−2(√(a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r)) Please correct me if i′m wrong

$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{cos}\:\theta=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}} \\ $$$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{cos}\:\theta=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$\mathrm{sin}\:\theta=\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Summarize}\:\mathrm{height}\:{h}={a}\:\mathrm{sin}\:\theta+{r} \\ $$$${h}={a}\:\mathrm{sin}\:\theta+{r}={a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r} \\ $$$$ \\ $$$$\mathrm{Calculate}\:\mathrm{time}\:\mathrm{with}\:\mathrm{equation} \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{height}\:\mathrm{equation}\:\mathrm{is}\:−{t}^{\mathrm{2}} +{h} \\ $$$$\mathrm{So}\:\mathrm{let}\:{f}\left({t}\right)=−{t}^{\mathrm{2}} +{h} \\ $$$${f}\left({t}\right)=−{t}^{\mathrm{2}} +{h}=\mathrm{0} \\ $$$${t}=\sqrt{{h}}\:\Rightarrow\:\mathrm{So},\:\mathrm{time}={t}=\sqrt{{a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}} \\ $$$$ \\ $$$$\mathrm{Calculate}\:\mathrm{speed}\:\mathrm{with}\:\mathrm{formula}\:{s}=\frac{{d}}{{dt}}{f}\left({t}\right) \\ $$$$\frac{{d}}{{dt}}{f}\left({t}\right)=\frac{{d}}{{dt}}\left(−{t}^{\mathrm{2}} +{h}\right)=−\mathrm{2}{t}\:\Rightarrow\:\mathrm{So},\:\mathrm{speed}=−\mathrm{2}{t}=−\mathrm{2}\sqrt{{a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}} \\ $$$$ \\ $$$$\mathrm{Please}\:\mathrm{correct}\:\mathrm{me}\:\mathrm{if}\:\mathrm{i}'\mathrm{m}\:\mathrm{wrong} \\ $$

Commented by MathematicalUser2357 last updated on 29/Nov/24

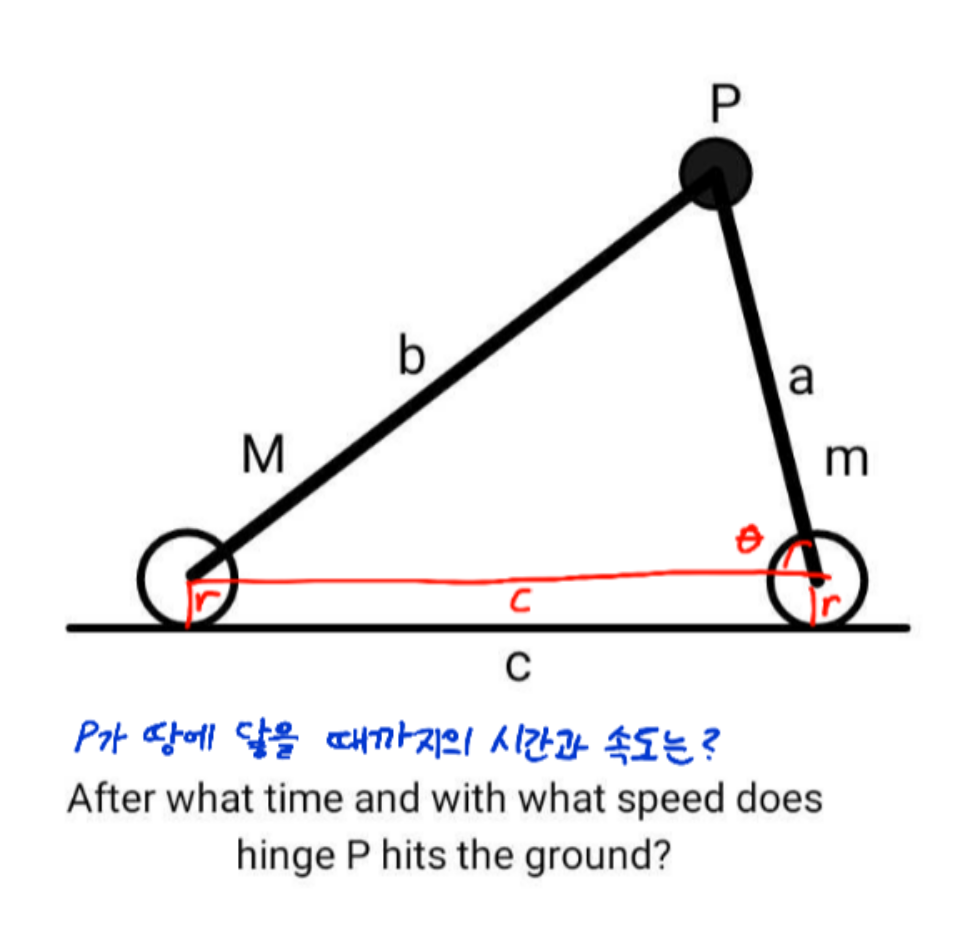
Commented by ajfour last updated on 29/Nov/24

−t^2 +h=0 how?

$$−{t}^{\mathrm{2}} +{h}=\mathrm{0} \\ $$$${how}? \\ $$$$ \\ $$

Commented by MathematicalUser2357 last updated on 29/Nov/24

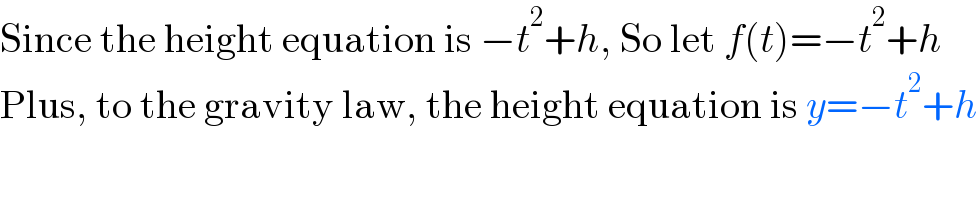
Since the height equation is −t^2 +h, So let f(t)=−t^2 +h Plus, to the gravity law, the height equation is y=−t^2 +h

$$\mathrm{Since}\:\mathrm{the}\:\mathrm{height}\:\mathrm{equation}\:\mathrm{is}\:−{t}^{\mathrm{2}} +{h},\:\mathrm{So}\:\mathrm{let}\:{f}\left({t}\right)=−{t}^{\mathrm{2}} +{h} \\ $$$$\mathrm{Plus},\:\mathrm{to}\:\mathrm{the}\:\mathrm{gravity}\:\mathrm{law},\:\mathrm{the}\:\mathrm{height}\:\mathrm{equation}\:\mathrm{is}\:{y}=−{t}^{\mathrm{2}} +{h} \\ $$

Commented by ajfour last updated on 29/Nov/24

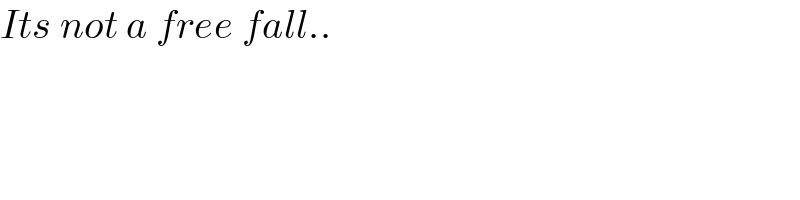
Its not a free fall..

$${Its}\:{not}\:{a}\:{free}\:{fall}.. \\ $$

Commented by MathematicalUser2357 last updated on 01/Dec/24

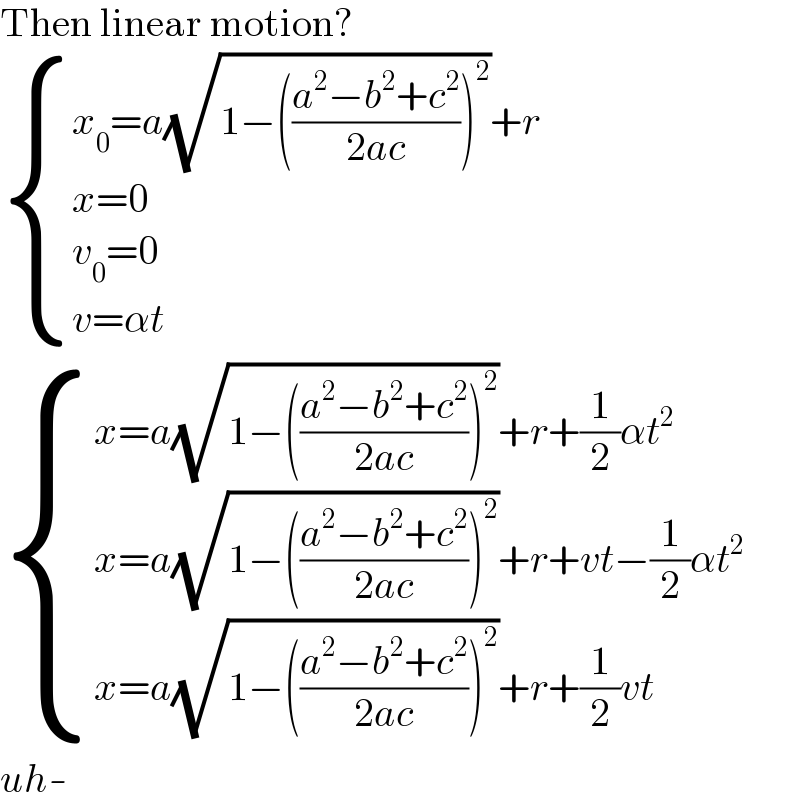
Then linear motion? { ((x_0 =a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r)),((x=0)),((v_0 =0)),((v=αt)) :} { ((x=a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r+(1/2)αt^2 )),((x=a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r+vt−(1/2)αt^2 )),((x=a(√(1−(((a^2 −b^2 +c^2 )/(2ac)))^2 ))+r+(1/2)vt)) :} uh-

$$\mathrm{Then}\:\mathrm{linear}\:\mathrm{motion}? \\ $$$$\begin{cases}{{x}_{\mathrm{0}} ={a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}}\\{{x}=\mathrm{0}}\\{{v}_{\mathrm{0}} =\mathrm{0}}\\{{v}=\alpha{t}}\end{cases} \\ $$$$\begin{cases}{{x}={a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}+\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} }\\{{x}={a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}+{vt}−\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} }\\{{x}={a}\sqrt{\mathrm{1}−\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{ac}}\right)^{\mathrm{2}} }+{r}+\frac{\mathrm{1}}{\mathrm{2}}{vt}}\end{cases} \\ $$$${uh}- \\ $$

Commented by mr W last updated on 01/Dec/24

Commented by mr W last updated on 03/Dec/24

this pucture shows the motions described in this question. for example you are standing on the top of such a twin ladder. sudently the spreaders connecting the ladders are brocken... the question is with what speed you hit the floor and what time do you take. the floor is slippery, no friction. i hope you didn′t get seriouly injured.

$${this}\:{pucture}\:{shows}\:{the}\: \\ $$$${motions}\:{described}\:{in}\:{this}\:{question}. \\ $$$${for}\:{example}\:{you}\:{are}\:{standing}\:{on} \\ $$$${the}\:{top}\:{of}\:{such}\:{a}\:{twin}\:{ladder}.\: \\ $$$${sudently}\:{the}\:{spreaders}\:{connecting}\: \\ $$$${the}\:{ladders}\:{are}\:{brocken}...\: \\ $$$${the}\:{question}\:{is}\:{with}\:{what}\:{speed}\:{you} \\ $$$${hit}\:{the}\:{floor}\:{and}\:{what}\:{time}\:{do}\:{you} \\ $$$${take}. \\ $$$${the}\:{floor}\:{is}\:{slippery},\:{no}\:{friction}. \\ $$$${i}\:{hope}\:{you}\:{didn}'{t}\:{get}\:{seriouly}\:{injured}. \\ $$

Answered by mr W last updated on 01/Dec/24

Commented by mr W last updated on 01/Dec/24

rods have uniform mass distribution. rod AP: length a, mass m_1 rod BP: length b, mass m_2 M=m_1 +m_2 say μ_1 =(m_1 /M), μ_2 =(m_2 /M) C=center of mass of both rods together h_C =height of C above ground=(h/2) at t=0: θ=θ_0 =cos^(−1) ((a^2 +b^2 −c^2 )/(2ab)) ((h_0 c)/2)=Δ_(ABP) =((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/4) ⇒h_0 =((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/(2c)) h_(C0) =(h_0 /2) at t=T: θ=π=180° at t: let ω=(dθ/dt) E, F are mass centers of rods EP=(a/2), FP=(b/2) AB=l=(√(a^2 +b^2 −2ab cos θ)) (dl/dθ)=((ab sin θ)/( (√(a^2 +b^2 −2ab cos θ))))=((ab sin θ)/l) EF=(l/2) EC=l_1 =(m_2 /(m_1 +m_2 ))×EF=((m_2 l)/(2M)) FC=l_2 =(m_1 /(m_1 +m_2 ))×EF=((m_1 l)/(2M)) point C moves only in vertical direction, because no force is acting in horizontal direction. ω_1 =(dϕ_1 /dt)=(dϕ_1 /dθ)×(dθ/dt)=ω(dϕ_1 /dθ) ω_2 =(dϕ_2 /dt)=(dϕ_2 /dθ)×(dθ/dt)=ω(dϕ_2 /dθ) ((sin ϕ_1 )/b)=((sin ϕ_2 )/a)=((sin θ)/( l)) ((cos ϕ_1 )/b)×(dϕ_1 /dθ)=((cos ϕ_2 )/a)×(dϕ_2 /dθ)=((cos θ)/l)−((sin θ)/l^2 )×(dl/dθ) ((cos ϕ_1 )/b)×(ω_1 /ω)=((cos ϕ_2 )/a)×(ω_2 /ω)=((cos θ)/l)−((ab sin^2 θ)/l^3 ) ω_1 =(cos θ−((ab sin^2 θ)/l^2 ))((ωb)/(l cos ϕ_1 )) ω_1 =(cos θ−((ab sin^2 θ)/l^2 ))((ωb)/( l(√(1− sin^2 ϕ_1 )))) ⇒ω_1 =(cos θ−((ab sin^2 θ)/l^2 ))(ω/( (√((l^2 /b^2 )− sin^2 θ)))) similarly ⇒ω_2 =(cos θ−((ab sin^2 θ)/l^2 ))(ω/( (√((l^2 /a^2 )− sin^2 θ)))) ((2h_C l)/2)=((ab sin θ)/2)=Δ_(ABP) ⇒h_C =((ab sin θ)/(2l)) (dh_C /dθ)=((ab)/2)(((cos θ)/l)−((sin θ)/l^2 )×(dl/dθ))=((ab)/(2l))(cos θ−((ab sin^2 θ)/l^2 )) u_(1x) =(dl_1 /dt)=((m_2 ω)/(2M))×(dl/dθ)=((m_2 ωab sin θ)/(2Ml)) u_(2x) =(dl_2 /dt)=((m_1 ω)/(2M))×(dl/dθ)=((m_1 ωab sin θ)/(2Ml)) u_(1y) =u_(2y) =−(dh_C /dt)=−ω(dh_C /dθ)=−((ωab)/(2l))(cos θ−((ab sin^2 θ)/l^2 )) loss of P.E.=gain of K.E. Mg(h_(C0) −h_C )=(1/2)m_1 (u_(1x) ^2 +u_(1y) ^2 )+(1/2)×((m_1 a^2 ω_1 ^2 )/(12)) +(1/2)m_2 (u_(2x) ^2 +u_(2y) ^2 )+(1/2)×((m_2 b^2 ω_2 ^2 )/(12)) 2Mg(h_(C0) −h_C )=Mu_(1y) ^2 +m_1 u_(1x) ^2 +m_2 u_(2x) ^2 +((m_1 a^2 ω_1 ^2 )/(12))+((m_2 b^2 ω_2 ^2 )/(12)) 2Mg(h_(C0) −h_C )=M(((ωab)/(2l)))^2 (cos θ−((ab sin^2 θ)/l^2 ))^2 +(m_1 m_2 ^2 +m_2 m_1 ^2 )(((ωab sin θ)/(2Ml)))^2 +((m_1 a^2 )/(12))×(cos θ−((ab sin^2 θ)/l^2 ))^2 ((ω^2 /( (l^2 /b^2 )− sin^2 θ)))+((m_2 b^2 )/(12))×(cos θ−((ab sin^2 θ)/l^2 ))^2 ((ω^2 /( (l^2 /b^2 )− sin^2 θ))) 8Mg(h_(C0) −((ab sin θ)/(2l)))=(cos θ−((ab sin^2 θ)/l^2 ))^2 ×((Ma^2 b^2 ω^2 )/l^2 )+((m_1 m_2 a^2 b^2 ω^2 sin^2 θ)/(Ml^2 )) +(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 (((m_1 a^2 )/( (l^2 /b^2 )− sin^2 θ))+((m_2 b^2 )/( (l^2 /b^2 )− sin^2 θ)))ω^2 4Mg(h_0 −((ab sin θ)/l))=((m_1 m_2 a^2 b^2 ω^2 sin^2 θ)/(Ml^2 ))+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 (((m_1 a^2 )/( (l^2 /b^2 )− sin^2 θ))+((m_2 b^2 )/( (l^2 /a^2 )− sin^2 θ))+((3Ma^2 b^2 )/l^2 ))ω^2 ω^2 =((4Mg(h_0 −((ab sin θ)/l)))/(((m_1 m_2 a^2 b^2 sin^2 θ)/(Ml^2 ))+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 (((m_1 a^2 )/( (l^2 /b^2 )− sin^2 θ))+((m_2 b^2 )/( (l^2 /a^2 )− sin^2 θ))+((3Ma^2 b^2 )/l^2 )))) ω=(√((4Mg(h_0 −((ab sin θ)/l)))/(((m_1 m_2 a^2 b^2 sin^2 θ)/(Ml^2 ))+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 (((m_1 a^2 )/( (l^2 /b^2 )− sin^2 θ))+((m_2 b^2 )/( (l^2 /a^2 )− sin^2 θ))+((3Ma^2 b^2 )/l^2 ))))) ⇒ω=(1/(ab))(√((4g(h_0 −((ab sin θ)/l)))/(((μ_1 μ_2 sin^2 θ)/l^2 )+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 ((μ_1 /( l^2 −b^2 sin^2 θ))+(μ_2 /( l^2 −a^2 sin^2 θ))+(3/l^2 ))))) dt=(dθ/ω) dt=ab(√((((μ_1 μ_2 sin^2 θ)/l^2 )+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 ((μ_1 /( l^2 −b^2 sin^2 θ))+(μ_2 /( l^2 −a^2 sin^2 θ))+(3/l^2 )))/(4g(h_0 −((ab sin θ)/l)))))dθ T=ab∫_θ_0 ^π (√((((μ_1 μ_2 sin^2 θ)/l^2 )+(1/3)(cos θ−((ab sin^2 θ)/l^2 ))^2 ((μ_1 /( l^2 −b^2 sin^2 θ))+(μ_2 /( l^2 −a^2 sin^2 θ))+(3/l^2 )))/(4g(h_0 −((ab sin θ)/l)))))dθ u_(Py) =a cos ϕ_1 ω_1 =a(((cos θ)/l)−((ab sin^2 θ)/l^3 ))bω ⇒u_(Py) =(cos θ−((ab sin^2 θ)/l^2 ))((ωab)/( l)) at t=T: θ=π ω=(((a+b)(√(3gh_0 )))/(ab)) u_(Py) =(√(3gh_0 )) >(√(2gh_0 )) recall: a ball released at point P hits the ground with a speed (√(2gh_0 )). ++++++++++ ω_1 =(cos θ−((ab sin^2 θ)/l^2 ))(ω/( (√((l^2 /b^2 )− sin^2 θ)))) α_1 =(dω_1 /dt)=(dω_1 /dθ)×(dθ/dt)=ω(dω_1 /dθ) −N_1 a cos ϕ_1 +m_1 g×((a cos ϕ_1 )/2)=((m_1 a^2 α_1 )/3) (N_1 /(m_1 g))=(1/2)−(a/(3g cos ϕ_1 ))×ω(dω_1 /dθ) (N_1 /(m_1 g))=(1/2)−((aω)/(3g(√(1−((b^2 sin^2 θ)/l^2 )))))×(dω_1 /dθ) similarly (N_2 /(m_2 g))=(1/2)−((bω)/(3g(√(1−((a^2 sin^2 θ)/l^2 )))))×(dω_2 /dθ)

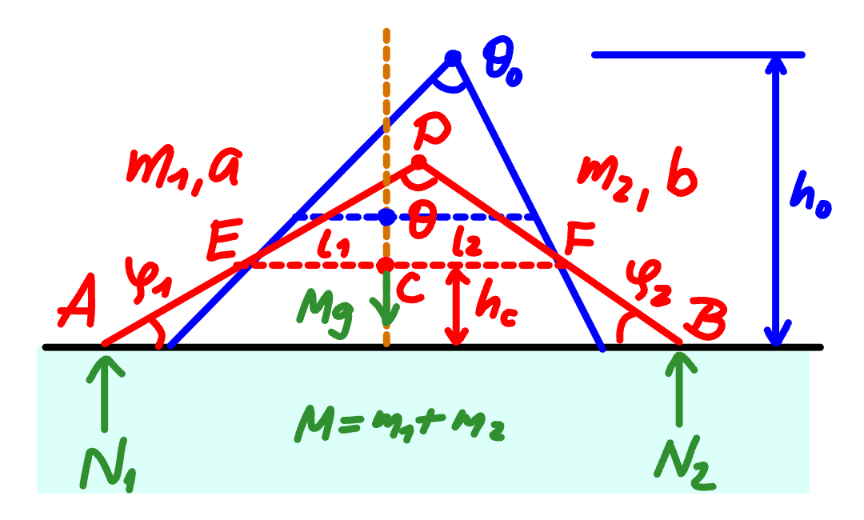
$${rods}\:{have}\:{uniform}\:{mass}\:{distribution}. \\ $$$${rod}\:{AP}:\:{length}\:{a},\:{mass}\:{m}_{\mathrm{1}} \\ $$$${rod}\:{BP}:\:{length}\:{b},\:{mass}\:{m}_{\mathrm{2}} \\ $$$${M}={m}_{\mathrm{1}} +{m}_{\mathrm{2}} \\ $$$${say}\:\mu_{\mathrm{1}} =\frac{{m}_{\mathrm{1}} }{{M}},\:\mu_{\mathrm{2}} =\frac{{m}_{\mathrm{2}} }{{M}} \\ $$$${C}={center}\:{of}\:{mass}\:{of}\:{both}\:{rods}\:{together} \\ $$$${h}_{{C}} ={height}\:{of}\:{C}\:{above}\:{ground}=\frac{{h}}{\mathrm{2}} \\ $$$$ \\ $$$${at}\:{t}=\mathrm{0}: \\ $$$$\theta=\theta_{\mathrm{0}} =\mathrm{cos}^{−\mathrm{1}} \frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\frac{{h}_{\mathrm{0}} {c}}{\mathrm{2}}=\Delta_{{ABP}} =\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{4}} \\ $$$$\Rightarrow{h}_{\mathrm{0}} =\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{2}{c}} \\ $$$${h}_{{C}\mathrm{0}} =\frac{{h}_{\mathrm{0}} }{\mathrm{2}} \\ $$$$ \\ $$$${at}\:{t}={T}: \\ $$$$\theta=\pi=\mathrm{180}° \\ $$$$ \\ $$$${at}\:{t}: \\ $$$${let}\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${E},\:{F}\:{are}\:{mass}\:{centers}\:{of}\:{rods} \\ $$$${EP}=\frac{{a}}{\mathrm{2}},\:{FP}=\frac{{b}}{\mathrm{2}} \\ $$$${AB}={l}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta} \\ $$$$\frac{{dl}}{{d}\theta}=\frac{{ab}\:\mathrm{sin}\:\theta}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta}}=\frac{{ab}\:\mathrm{sin}\:\theta}{{l}} \\ $$$${EF}=\frac{{l}}{\mathrm{2}} \\ $$$${EC}={l}_{\mathrm{1}} =\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }×{EF}=\frac{{m}_{\mathrm{2}} {l}}{\mathrm{2}{M}} \\ $$$${FC}={l}_{\mathrm{2}} =\frac{{m}_{\mathrm{1}} }{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }×{EF}=\frac{{m}_{\mathrm{1}} {l}}{\mathrm{2}{M}} \\ $$$${point}\:{C}\:{moves}\:{only}\:{in}\:{vertical} \\ $$$${direction},\:{because}\:{no}\:{force}\:{is}\:{acting} \\ $$$${in}\:{horizontal}\:{direction}. \\ $$$$\omega_{\mathrm{1}} =\frac{{d}\varphi_{\mathrm{1}} }{{dt}}=\frac{{d}\varphi_{\mathrm{1}} }{{d}\theta}×\frac{{d}\theta}{{dt}}=\omega\frac{{d}\varphi_{\mathrm{1}} }{{d}\theta} \\ $$$$\omega_{\mathrm{2}} =\frac{{d}\varphi_{\mathrm{2}} }{{dt}}=\frac{{d}\varphi_{\mathrm{2}} }{{d}\theta}×\frac{{d}\theta}{{dt}}=\omega\frac{{d}\varphi_{\mathrm{2}} }{{d}\theta} \\ $$$$\frac{\mathrm{sin}\:\varphi_{\mathrm{1}} }{{b}}=\frac{\mathrm{sin}\:\varphi_{\mathrm{2}} }{{a}}=\frac{\mathrm{sin}\:\theta}{\:{l}} \\ $$$$\frac{\mathrm{cos}\:\varphi_{\mathrm{1}} }{{b}}×\frac{{d}\varphi_{\mathrm{1}} }{{d}\theta}=\frac{\mathrm{cos}\:\varphi_{\mathrm{2}} }{{a}}×\frac{{d}\varphi_{\mathrm{2}} }{{d}\theta}=\frac{\mathrm{cos}\:\theta}{{l}}−\frac{\mathrm{sin}\:\theta}{{l}^{\mathrm{2}} }×\frac{{dl}}{{d}\theta} \\ $$$$\frac{\mathrm{cos}\:\varphi_{\mathrm{1}} }{{b}}×\frac{\omega_{\mathrm{1}} }{\omega}=\frac{\mathrm{cos}\:\varphi_{\mathrm{2}} }{{a}}×\frac{\omega_{\mathrm{2}} }{\omega}=\frac{\mathrm{cos}\:\theta}{{l}}−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{3}} } \\ $$$$\omega_{\mathrm{1}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega{b}}{{l}\:\mathrm{cos}\:\varphi_{\mathrm{1}} } \\ $$$$\omega_{\mathrm{1}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega{b}}{\:{l}\sqrt{\mathrm{1}−\:\mathrm{sin}^{\mathrm{2}} \:\varphi_{\mathrm{1}} }} \\ $$$$\Rightarrow\omega_{\mathrm{1}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$${similarly} \\ $$$$\Rightarrow\omega_{\mathrm{2}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\frac{\mathrm{2}{h}_{{C}} {l}}{\mathrm{2}}=\frac{{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}}=\Delta_{{ABP}} \\ $$$$\Rightarrow{h}_{{C}} =\frac{{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}{l}} \\ $$$$\frac{{dh}_{{C}} }{{d}\theta}=\frac{{ab}}{\mathrm{2}}\left(\frac{\mathrm{cos}\:\theta}{{l}}−\frac{\mathrm{sin}\:\theta}{{l}^{\mathrm{2}} }×\frac{{dl}}{{d}\theta}\right)=\frac{{ab}}{\mathrm{2}{l}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right) \\ $$$${u}_{\mathrm{1}{x}} =\frac{{dl}_{\mathrm{1}} }{{dt}}=\frac{{m}_{\mathrm{2}} \omega}{\mathrm{2}{M}}×\frac{{dl}}{{d}\theta}=\frac{{m}_{\mathrm{2}} \omega{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}{Ml}} \\ $$$${u}_{\mathrm{2}{x}} =\frac{{dl}_{\mathrm{2}} }{{dt}}=\frac{{m}_{\mathrm{1}} \omega}{\mathrm{2}{M}}×\frac{{dl}}{{d}\theta}=\frac{{m}_{\mathrm{1}} \omega{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}{Ml}} \\ $$$${u}_{\mathrm{1}{y}} ={u}_{\mathrm{2}{y}} =−\frac{{dh}_{{C}} }{{dt}}=−\omega\frac{{dh}_{{C}} }{{d}\theta}=−\frac{\omega{ab}}{\mathrm{2}{l}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right) \\ $$$${loss}\:{of}\:{P}.{E}.={gain}\:{of}\:{K}.{E}. \\ $$$${Mg}\left({h}_{{C}\mathrm{0}} −{h}_{{C}} \right)=\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}} \left({u}_{\mathrm{1}{x}} ^{\mathrm{2}} +{u}_{\mathrm{1}{y}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} \omega_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{2}} \left({u}_{\mathrm{2}{x}} ^{\mathrm{2}} +{u}_{\mathrm{2}{y}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} \omega_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\mathrm{2}{Mg}\left({h}_{{C}\mathrm{0}} −{h}_{{C}} \right)={Mu}_{\mathrm{1}{y}} ^{\mathrm{2}} +{m}_{\mathrm{1}} {u}_{\mathrm{1}{x}} ^{\mathrm{2}} +{m}_{\mathrm{2}} {u}_{\mathrm{2}{x}} ^{\mathrm{2}} +\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} \omega_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{12}}+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} \omega_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\mathrm{2}{Mg}\left({h}_{{C}\mathrm{0}} −{h}_{{C}} \right)={M}\left(\frac{\omega{ab}}{\mathrm{2}{l}}\right)^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left({m}_{\mathrm{1}} {m}_{\mathrm{2}} ^{\mathrm{2}} +{m}_{\mathrm{2}} {m}_{\mathrm{1}} ^{\mathrm{2}} \right)\left(\frac{\omega{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}{Ml}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} }{\mathrm{12}}×\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\omega^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}\right)+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{12}}×\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\omega^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}\right) \\ $$$$\mathrm{8}{Mg}\left({h}_{{C}\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}{l}}\right)=\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} ×\frac{{Ma}^{\mathrm{2}} {b}^{\mathrm{2}} \omega^{\mathrm{2}} }{{l}^{\mathrm{2}} }+\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{Ml}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}\right)\omega^{\mathrm{2}} \\ $$$$\mathrm{4}{Mg}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)=\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{Ml}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}{Ma}^{\mathrm{2}} {b}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right)\omega^{\mathrm{2}} \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{4}{Mg}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)}{\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{Ml}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}{Ma}^{\mathrm{2}} {b}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right)} \\ $$$$\omega=\sqrt{\frac{\mathrm{4}{Mg}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)}{\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{Ml}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{{m}_{\mathrm{2}} {b}^{\mathrm{2}} }{\:\frac{{l}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}{Ma}^{\mathrm{2}} {b}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right)}} \\ $$$$\Rightarrow\omega=\frac{\mathrm{1}}{{ab}}\sqrt{\frac{\mathrm{4}{g}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)}{\frac{\mu_{\mathrm{1}} \mu_{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\mu_{\mathrm{1}} }{\:{l}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mu_{\mathrm{2}} }{\:{l}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}}{{l}^{\mathrm{2}} }\right)}} \\ $$$${dt}=\frac{{d}\theta}{\omega} \\ $$$${dt}={ab}\sqrt{\frac{\frac{\mu_{\mathrm{1}} \mu_{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\mu_{\mathrm{1}} }{\:{l}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mu_{\mathrm{2}} }{\:{l}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}}{{l}^{\mathrm{2}} }\right)}{\mathrm{4}{g}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)}}{d}\theta \\ $$$${T}={ab}\int_{\theta_{\mathrm{0}} } ^{\pi} \sqrt{\frac{\frac{\mu_{\mathrm{1}} \mu_{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\mu_{\mathrm{1}} }{\:{l}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mu_{\mathrm{2}} }{\:{l}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}+\frac{\mathrm{3}}{{l}^{\mathrm{2}} }\right)}{\mathrm{4}{g}\left({h}_{\mathrm{0}} −\frac{{ab}\:\mathrm{sin}\:\theta}{{l}}\right)}}{d}\theta \\ $$$${u}_{{Py}} ={a}\:\mathrm{cos}\:\varphi_{\mathrm{1}} \:\omega_{\mathrm{1}} ={a}\left(\frac{\mathrm{cos}\:\theta}{{l}}−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{3}} }\right){b}\omega \\ $$$$\Rightarrow{u}_{{Py}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega{ab}}{\:{l}} \\ $$$$ \\ $$$${at}\:{t}={T}: \\ $$$$\theta=\pi \\ $$$$\omega=\frac{\left({a}+{b}\right)\sqrt{\mathrm{3}{gh}_{\mathrm{0}} }}{{ab}} \\ $$$${u}_{{Py}} =\sqrt{\mathrm{3}{gh}_{\mathrm{0}} }\:>\sqrt{\mathrm{2}{gh}_{\mathrm{0}} } \\ $$$${recall}:\:{a}\:{ball}\:{released}\:{at}\:{point}\:{P} \\ $$$${hits}\:{the}\:{ground}\:{with}\:{a}\:{speed}\:\sqrt{\mathrm{2}{gh}_{\mathrm{0}} }. \\ $$$$++++++++++ \\ $$$$\omega_{\mathrm{1}} =\left(\mathrm{cos}\:\theta−\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }\right)\frac{\omega}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\alpha_{\mathrm{1}} =\frac{{d}\omega_{\mathrm{1}} }{{dt}}=\frac{{d}\omega_{\mathrm{1}} }{{d}\theta}×\frac{{d}\theta}{{dt}}=\omega\frac{{d}\omega_{\mathrm{1}} }{{d}\theta} \\ $$$$−{N}_{\mathrm{1}} {a}\:\mathrm{cos}\:\varphi_{\mathrm{1}} +{m}_{\mathrm{1}} {g}×\frac{{a}\:\mathrm{cos}\:\varphi_{\mathrm{1}} }{\mathrm{2}}=\frac{{m}_{\mathrm{1}} {a}^{\mathrm{2}} \alpha_{\mathrm{1}} }{\mathrm{3}} \\ $$$$\frac{{N}_{\mathrm{1}} }{{m}_{\mathrm{1}} {g}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{{a}}{\mathrm{3}{g}\:\mathrm{cos}\:\varphi_{\mathrm{1}} }×\omega\frac{{d}\omega_{\mathrm{1}} }{{d}\theta} \\ $$$$\frac{{N}_{\mathrm{1}} }{{m}_{\mathrm{1}} {g}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{{a}\omega}{\mathrm{3}{g}\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }}}×\frac{{d}\omega_{\mathrm{1}} }{{d}\theta} \\ $$$${similarly} \\ $$$$\frac{{N}_{\mathrm{2}} }{{m}_{\mathrm{2}} {g}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{{b}\omega}{\mathrm{3}{g}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{{l}^{\mathrm{2}} }}}×\frac{{d}\omega_{\mathrm{2}} }{{d}\theta} \\ $$

Commented by mr W last updated on 30/Nov/24

Commented by mr W last updated on 30/Nov/24

in all these cases the point P hits the ground with the same speed regardless which relation the lengthes and the masses of the rods have.

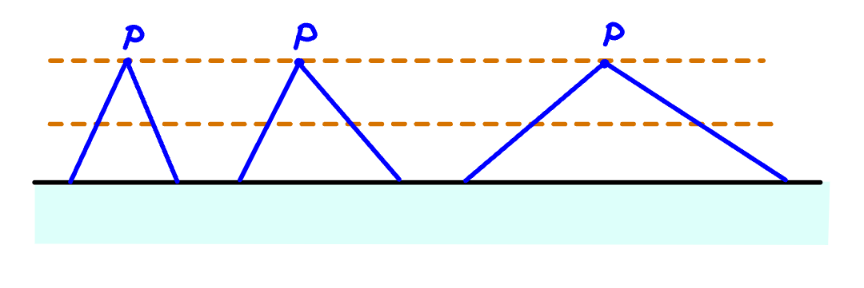
$${in}\:{all}\:{these}\:{cases}\:{the}\:{point}\:{P}\:{hits} \\ $$$${the}\:{ground}\:{with}\:{the}\:{same}\:{speed} \\ $$$${regardless}\:{which}\:{relation}\:{the} \\ $$$${lengthes}\:{and}\:{the}\:{masses}\:{of}\:{the}\:{rods} \\ $$$${have}. \\ $$

Commented by mr W last updated on 30/Nov/24

Commented by mr W last updated on 30/Nov/24

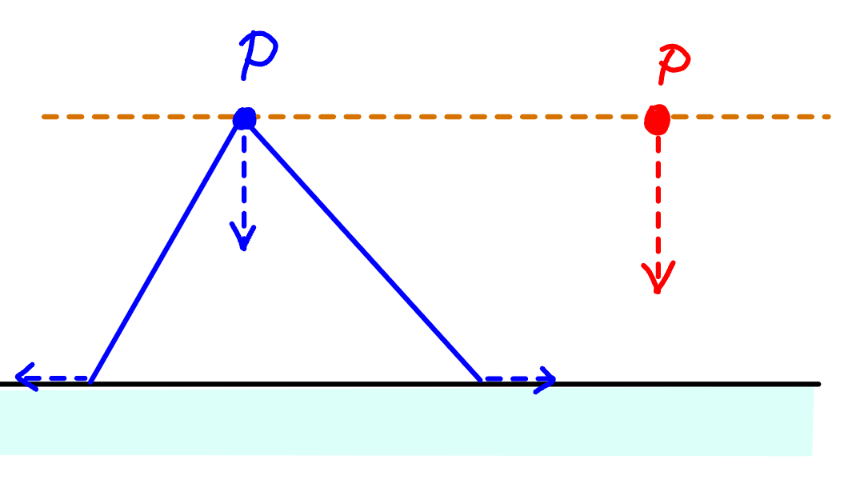
how is it possible that the point P hits the ground with a larger speed than a ball from the same height?

$${how}\:{is}\:{it}\:{possible}\:{that}\:{the}\:{point}\:{P} \\ $$$${hits}\:{the}\:{ground}\:{with}\:{a}\:{larger}\:{speed} \\ $$$${than}\:{a}\:{ball}\:{from}\:{the}\:{same}\:{height}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com