Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 214100 by ajfour last updated on 28/Nov/24

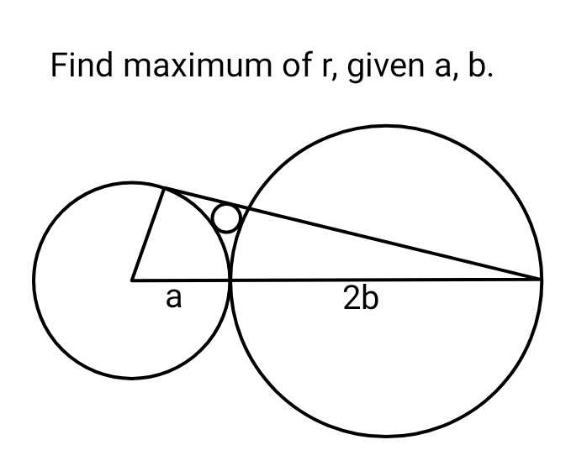
Answered by ajfour last updated on 29/Nov/24

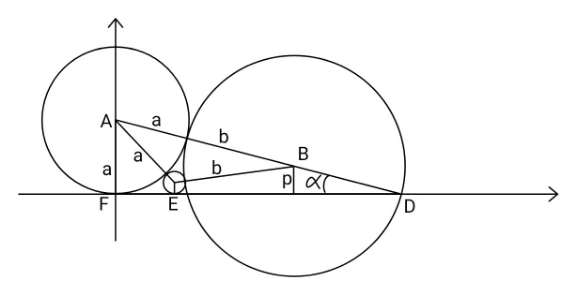
Commented by ajfour last updated on 29/Nov/24

sin α=(a/(2b+a))=(1/(2s+1)) ∀ s=(b/a), t=(r/a) A=2(√(ar)) B=(√((b+r)^2 −(p−r)^2 )) A+B=(a+b)cos α B^2 ={A−(a+b)cos α}^2 b^2 −p^2 +2r(b+p) =4ar+(a+b)^2 cos^2 α−4(√(ar))(a+b)cos α as p=bsin α 2rb(1+sin α)+4(a+b)(√(ar))cos α =4ar+a^2 cos^2 α+2abcos^2 α recalling s=(b/a), t=(r/a) 2t(s+ssin α−2)+4(1+s)(√t)cos α −(1+2s)cos^2 α =0 (√t)=−(((1+s)cos α)/(s+ssin α−2))±(√(((((1+s)cos α)/(s+ssin α−2)))^2 +(((1+2s)cos^2 α)/(2(s+ssin α−2))))) say a=1, b=2 ⇒ s=2, sin α=(1/5), cos α=((2(√6))/5) (√t)=−3(√6)+2(√(15)) r=t=114−36(√(10)) ⇒ r≈ 0.1580

$$\mathrm{sin}\:\alpha=\frac{{a}}{\mathrm{2}{b}+{a}}=\frac{\mathrm{1}}{\mathrm{2}{s}+\mathrm{1}}\:\:\:\forall\:\:{s}=\frac{{b}}{{a}},\:{t}=\frac{{r}}{{a}} \\ $$$${A}=\mathrm{2}\sqrt{{ar}} \\ $$$${B}=\sqrt{\left({b}+{r}\right)^{\mathrm{2}} −\left({p}−{r}\right)^{\mathrm{2}} } \\ $$$${A}+{B}=\left({a}+{b}\right)\mathrm{cos}\:\alpha \\ $$$${B}^{\mathrm{2}} =\left\{{A}−\left({a}+{b}\right)\mathrm{cos}\:\alpha\right\}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} −{p}^{\mathrm{2}} +\mathrm{2}{r}\left({b}+{p}\right) \\ $$$$=\mathrm{4}{ar}+\left({a}+{b}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha−\mathrm{4}\sqrt{{ar}}\left({a}+{b}\right)\mathrm{cos}\:\alpha \\ $$$${as}\:\:{p}={b}\mathrm{sin}\:\alpha \\ $$$$\mathrm{2}{rb}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)+\mathrm{4}\left({a}+{b}\right)\sqrt{{ar}}\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}{ar}+{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{2}{ab}\mathrm{cos}\:^{\mathrm{2}} \alpha \\ $$$${recalling}\:\:{s}=\frac{{b}}{{a}},\:{t}=\frac{{r}}{{a}} \\ $$$$\mathrm{2}{t}\left({s}+{s}\mathrm{sin}\:\alpha−\mathrm{2}\right)+\mathrm{4}\left(\mathrm{1}+{s}\right)\sqrt{{t}}\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{1}+\mathrm{2}{s}\right)\mathrm{cos}\:^{\mathrm{2}} \alpha\:=\mathrm{0} \\ $$$$\sqrt{{t}}=−\frac{\left(\mathrm{1}+{s}\right)\mathrm{cos}\:\alpha}{{s}+{s}\mathrm{sin}\:\alpha−\mathrm{2}}\pm\sqrt{\left(\frac{\left(\mathrm{1}+{s}\right)\mathrm{cos}\:\alpha}{{s}+{s}\mathrm{sin}\:\alpha−\mathrm{2}}\right)^{\mathrm{2}} +\frac{\left(\mathrm{1}+\mathrm{2}{s}\right)\mathrm{cos}\:^{\mathrm{2}} \alpha}{\mathrm{2}\left({s}+{s}\mathrm{sin}\:\alpha−\mathrm{2}\right)}} \\ $$$${say}\:{a}=\mathrm{1},\:{b}=\mathrm{2}\:\: \\ $$$$\Rightarrow\:{s}=\mathrm{2},\:\:\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{5}},\:\:\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}} \\ $$$$\sqrt{{t}}=−\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{2}\sqrt{\mathrm{15}} \\ $$$${r}={t}=\mathrm{114}−\mathrm{36}\sqrt{\mathrm{10}} \\ $$$$\Rightarrow\:\:{r}\approx\:\mathrm{0}.\mathrm{1580}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by mr W last updated on 29/Nov/24

p=((ab)/(a+2b)) (√((a+b)^2 −(a−p)^2 ))=(√((a+r)^2 −(a−r)^2 ))+(√((b+r)^2 −(p−r)^2 )) (√(b^2 +2ab+2ap−p^2 ))=2(√(ar))+(√(b^2 −p^2 +2(b+p)r)) (√(b^2 +2ab+2ap−p^2 ))−2(√(ar))=(√(b^2 −p^2 +2(b+p)r)) (2a−b−p)r−2(√(a(b+p)(2a+b−p)r))+a(b+p)=0 (√r)=(((√(a(b+p)(2a+b−p)))−(√(a(b+p)(2a+b−p)−a(b+p)(2a−b−p))))/(2a−b−p)) (√r)=(((√(a(b+p)))((√(2a+b−p))−(√(2b))))/(2a−b−p)) r=((a(b+p)((√(2a+b−p))−(√(2b)))^2 )/((2a−b−p)^2 )) r=((a(b+((ab)/(a+2b)))((√(2a+b−((ab)/(a+2b))))−(√(2b)))^2 )/((2a−b−((ab)/(a+2b)))^2 )) r=((ab(a+b)((√(a^2 +ab+b^2 ))−(√((a+2b)b)))^2 )/((a^2 +ab−b^2 )^2 )) r=((ab(a+b)[a^2 +2ab+3b^2 −2(√(b(a+2b)(a^2 +ab+b^2 )))])/((a^2 +ab−b^2 )^2 ))

$${p}=\frac{{ab}}{{a}+\mathrm{2}{b}} \\ $$$$\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{p}\right)^{\mathrm{2}} }=\sqrt{\left({a}+{r}\right)^{\mathrm{2}} −\left({a}−{r}\right)^{\mathrm{2}} }+\sqrt{\left({b}+{r}\right)^{\mathrm{2}} −\left({p}−{r}\right)^{\mathrm{2}} } \\ $$$$\sqrt{{b}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{2}{ap}−{p}^{\mathrm{2}} }=\mathrm{2}\sqrt{{ar}}+\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} +\mathrm{2}\left({b}+{p}\right){r}} \\ $$$$\sqrt{{b}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{2}{ap}−{p}^{\mathrm{2}} }−\mathrm{2}\sqrt{{ar}}=\sqrt{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} +\mathrm{2}\left({b}+{p}\right){r}} \\ $$$$\left(\mathrm{2}{a}−{b}−{p}\right){r}−\mathrm{2}\sqrt{{a}\left({b}+{p}\right)\left(\mathrm{2}{a}+{b}−{p}\right){r}}+{a}\left({b}+{p}\right)=\mathrm{0} \\ $$$$\sqrt{{r}}=\frac{\sqrt{{a}\left({b}+{p}\right)\left(\mathrm{2}{a}+{b}−{p}\right)}−\sqrt{{a}\left({b}+{p}\right)\left(\mathrm{2}{a}+{b}−{p}\right)−{a}\left({b}+{p}\right)\left(\mathrm{2}{a}−{b}−{p}\right)}}{\mathrm{2}{a}−{b}−{p}} \\ $$$$\sqrt{{r}}=\frac{\sqrt{{a}\left({b}+{p}\right)}\left(\sqrt{\mathrm{2}{a}+{b}−{p}}−\sqrt{\mathrm{2}{b}}\right)}{\mathrm{2}{a}−{b}−{p}} \\ $$$${r}=\frac{{a}\left({b}+{p}\right)\left(\sqrt{\mathrm{2}{a}+{b}−{p}}−\sqrt{\mathrm{2}{b}}\right)^{\mathrm{2}} }{\left(\mathrm{2}{a}−{b}−{p}\right)^{\mathrm{2}} } \\ $$$${r}=\frac{{a}\left({b}+\frac{{ab}}{{a}+\mathrm{2}{b}}\right)\left(\sqrt{\mathrm{2}{a}+{b}−\frac{{ab}}{{a}+\mathrm{2}{b}}}−\sqrt{\mathrm{2}{b}}\right)^{\mathrm{2}} }{\left(\mathrm{2}{a}−{b}−\frac{{ab}}{{a}+\mathrm{2}{b}}\right)^{\mathrm{2}} } \\ $$$${r}=\frac{{ab}\left({a}+{b}\right)\left(\sqrt{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }−\sqrt{\left({a}+\mathrm{2}{b}\right){b}}\right)^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${r}=\frac{{ab}\left({a}+{b}\right)\left[{a}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{3}{b}^{\mathrm{2}} −\mathrm{2}\sqrt{{b}\left({a}+\mathrm{2}{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}\right]}{\left({a}^{\mathrm{2}} +{ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$

Commented by ajfour last updated on 29/Nov/24

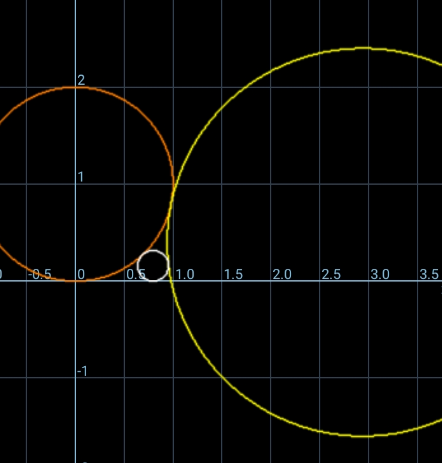
Commented by ajfour last updated on 29/Nov/24

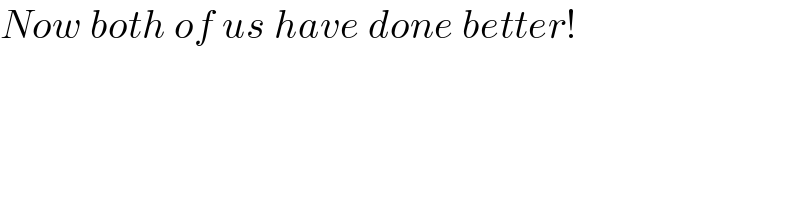
Now both of us have done better!

$${Now}\:{both}\:{of}\:{us}\:{have}\:{done}\:{better}! \\ $$

Answered by mr W last updated on 28/Nov/24

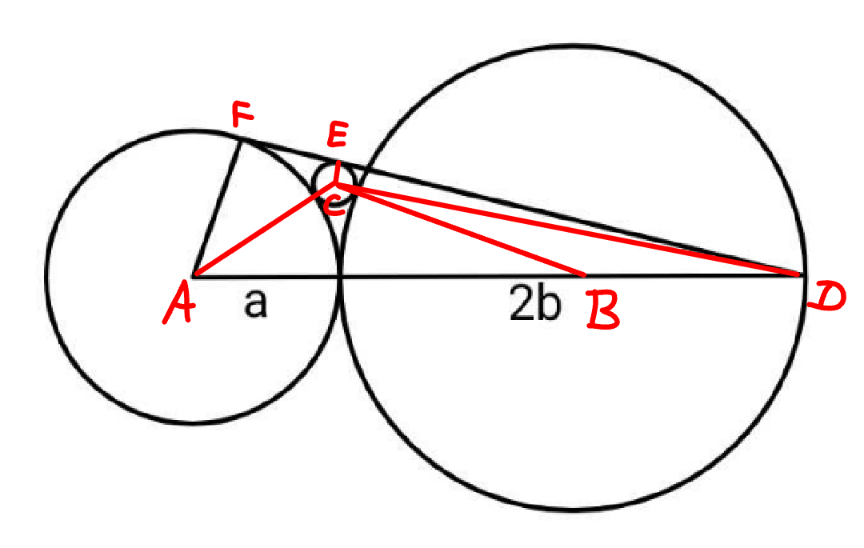
Commented by mr W last updated on 28/Nov/24

for maximum small circle: AF⊥FD FE=(√((a+r)^2 −(a−r)^2 ))=2(√(ar)) (a+b)CD^2 +b(a+r)^2 =(a+2b)[(b+r)^2 +(a+b)b] CD^2 =(((a+2b)[(b+r)^2 +(a+b)b]−b(a+r)^2 )/(a+b)) ED=(√((((a+2b)[(b+r)^2 +(a+b)b]−b(a+r)^2 )/(a+b))−r^2 )) FD=2(√(ar))+(√((((a+2b)[(b+r)^2 +(a+b)b]−b(a+r)^2 )/(a+b))−r^2 )) FD^2 =a^2 +(a+2b)^2 ⇒{2(√(ar))+(√((((a+2b)[(b+r)^2 +(a+b)b]−b(a+r)^2 )/(a+b))−r^2 ))}^2 =a^2 +(a+2b)^2

$${for}\:{maximum}\:{small}\:{circle}: \\ $$$${AF}\bot{FD} \\ $$$${FE}=\sqrt{\left({a}+{r}\right)^{\mathrm{2}} −\left({a}−{r}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{ar}} \\ $$$$\left({a}+{b}\right){CD}^{\mathrm{2}} +{b}\left({a}+{r}\right)^{\mathrm{2}} =\left({a}+\mathrm{2}{b}\right)\left[\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{b}\right){b}\right] \\ $$$${CD}^{\mathrm{2}} =\frac{\left({a}+\mathrm{2}{b}\right)\left[\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{b}\right){b}\right]−{b}\left({a}+{r}\right)^{\mathrm{2}} }{{a}+{b}} \\ $$$${ED}=\sqrt{\frac{\left({a}+\mathrm{2}{b}\right)\left[\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{b}\right){b}\right]−{b}\left({a}+{r}\right)^{\mathrm{2}} }{{a}+{b}}−{r}^{\mathrm{2}} } \\ $$$${FD}=\mathrm{2}\sqrt{{ar}}+\sqrt{\frac{\left({a}+\mathrm{2}{b}\right)\left[\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{b}\right){b}\right]−{b}\left({a}+{r}\right)^{\mathrm{2}} }{{a}+{b}}−{r}^{\mathrm{2}} } \\ $$$${FD}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left\{\mathrm{2}\sqrt{{ar}}+\sqrt{\frac{\left({a}+\mathrm{2}{b}\right)\left[\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{b}\right){b}\right]−{b}\left({a}+{r}\right)^{\mathrm{2}} }{{a}+{b}}−{r}^{\mathrm{2}} }\right\}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com