
Question Number 214093 by ajfour last updated on 27/Nov/24
Commented by ajfour last updated on 27/Nov/24
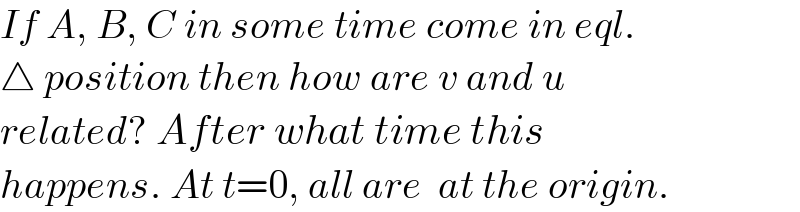
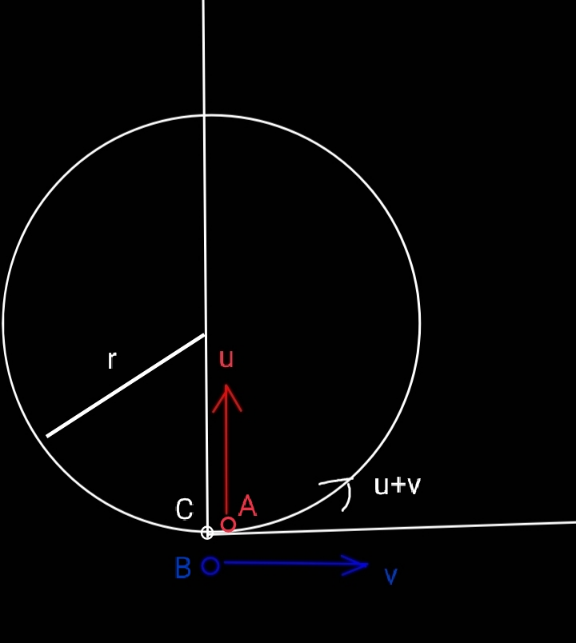
$${If}\:{A},\:{B},\:{C}\:{in}\:{some}\:{time}\:{come}\:{in}\:{eql}. \\ $$$$\bigtriangleup\:{position}\:{then}\:{how}\:{are}\:{v}\:{and}\:{u} \\ $$$${related}?\:{After}\:{what}\:{time}\:{this} \\ $$$${happens}.\:{At}\:{t}=\mathrm{0},\:{all}\:{are}\:\:{at}\:{the}\:{origin}. \\ $$
Answered by ajfour last updated on 28/Nov/24
![y_A =ut , x_B =vt x_C =Rsin{(((u+v)t)/R)} y_C =R−Rcos {(((u+v)t)/R)} M(((vt)/2), ((ut)/2)) tan φ=(u/v) line MC y−((ut)/2)=(u/v)(x−((vt)/2)) R−Rcos {(((u+v)t)/R)} =((ut)/2)+(u/v)[Rsin{(((u+v)t)/R)}−((vt)/2)] say ω=((u+v)/R) v(1−cos ωt)=usin ωt then we also must have {Rsin (ωt)−((vt)/2)}^2 +{R−Rcos (ωt)−((ut)/2)}^2 =(((3t^2 )/4))(u^2 +v^2 ) ⇒ {Rsin (ωt)−((vt)/2)}(√(1+(v^2 /u^2 )))=(((√3)/2)t)(√(u^2 +v^2 )) Rsin (ωt)−((vt)/2)=(((√3)ut)/2) ⇒ {v−u((((√3)u+v)/(2R)))t}^2 =v^2 −v^2 ((((√3)u+v)/(2R)))^2 t^2 ⇒ 2uv=((((√3)u+v)/(2R)))t(u^2 +v^2 ) ⇒ t=((4uvR)/((u^2 +v^2 )((√3)u+v))) ...](Q214095.png)
$${y}_{{A}} ={ut}\:\:,\:\:{x}_{{B}} ={vt} \\ $$$${x}_{{C}} ={R}\mathrm{sin}\left\{\frac{\left({u}+{v}\right){t}}{{R}}\right\} \\ $$$${y}_{{C}} ={R}−{R}\mathrm{cos}\:\left\{\frac{\left({u}+{v}\right){t}}{{R}}\right\} \\ $$$${M}\left(\frac{{vt}}{\mathrm{2}},\:\frac{{ut}}{\mathrm{2}}\right) \\ $$$$\mathrm{tan}\:\phi=\frac{{u}}{{v}} \\ $$$${line}\:{MC} \\ $$$${y}−\frac{{ut}}{\mathrm{2}}=\frac{{u}}{{v}}\left({x}−\frac{{vt}}{\mathrm{2}}\right) \\ $$$${R}−{R}\mathrm{cos}\:\left\{\frac{\left({u}+{v}\right){t}}{{R}}\right\} \\ $$$$\:\:\:\:\:\:=\frac{{ut}}{\mathrm{2}}+\frac{{u}}{{v}}\left[{R}\mathrm{sin}\left\{\frac{\left({u}+{v}\right){t}}{{R}}\right\}−\frac{{vt}}{\mathrm{2}}\right] \\ $$$${say}\:\omega=\frac{{u}+{v}}{{R}}\: \\ $$$${v}\left(\mathrm{1}−\mathrm{cos}\:\omega{t}\right)={u}\mathrm{sin}\:\omega{t} \\ $$$$\:\:{then}\:{we}\:{also}\:{must}\:{have} \\ $$$$\left\{{R}\mathrm{sin}\:\left(\omega{t}\right)−\frac{{vt}}{\mathrm{2}}\right\}^{\mathrm{2}} +\left\{{R}−{R}\mathrm{cos}\:\left(\omega{t}\right)−\frac{{ut}}{\mathrm{2}}\right\}^{\mathrm{2}} \\ $$$$\:\:\:=\left(\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{4}}\right)\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\left\{{R}\mathrm{sin}\:\left(\omega{t}\right)−\frac{{vt}}{\mathrm{2}}\right\}\sqrt{\mathrm{1}+\frac{{v}^{\mathrm{2}} }{{u}^{\mathrm{2}} }}=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}\right)\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} } \\ $$$$\:{R}\mathrm{sin}\:\left(\omega{t}\right)−\frac{{vt}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{ut}}{\mathrm{2}} \\ $$$$\Rightarrow\:\left\{{v}−{u}\left(\frac{\sqrt{\mathrm{3}}{u}+{v}}{\mathrm{2}{R}}\right){t}\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={v}^{\mathrm{2}} −{v}^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{3}}{u}+{v}}{\mathrm{2}{R}}\right)^{\mathrm{2}} {t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{uv}=\left(\frac{\sqrt{\mathrm{3}}{u}+{v}}{\mathrm{2}{R}}\right){t}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{t}=\frac{\mathrm{4}{uvR}}{\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{3}}{u}+{v}\right)} \\ $$$$... \\ $$
Answered by mr W last updated on 28/Nov/24
![say s=side length of equilateral at time t: x_A =0, y_A =ut x_B =vt, y_B =0 x_C =r sin (((u+v)t)/r), y_C =r(1−cos (((u+v)t)/r)) let α=((ut)/r), β=((vt)/r), λ=(s/r) AB^2 =s^2 =(ut)^2 +(vt)^2 ⇒λ^2 =α^2 +β^2 ...(i) AC^2 =s^2 =r^2 sin^2 (((u+v)t)/r)+(r−r cos (((u+v)t)/r)−ut)^2 ⇒λ^2 = sin^2 (α+β)+[1−cos (α+β)−α]^2 ...(ii) BC^2 =s^2 =(r sin (((u+v)t)/r)−vt)^2 +(r−r cos (((u+v)t)/r))^2 ⇒λ^2 =[sin (α+β)−β]^2 +[1−cos (α+β)]^2 ...(iii) (i) and (ii): sin^2 (α+β)+[1−cos (α+β)−α]^2 =α^2 +β^2 ⇒(1−α)[1−cos (α+β)]=(β^2 /2) ...(I) (i) and (iii): [sin (α+β)−β]^2 +[1−cos (α+β)]^2 =α^2 +β^2 ⇒cos (α+β)+β sin (α+β)=1−(α^2 /2) ...(II)](Q214105.png)
$${say}\:{s}={side}\:{length}\:{of}\:{equilateral} \\ $$$${at}\:{time}\:{t}: \\ $$$${x}_{{A}} =\mathrm{0},\:{y}_{{A}} ={ut} \\ $$$${x}_{{B}} ={vt},\:{y}_{{B}} =\mathrm{0} \\ $$$${x}_{{C}} ={r}\:\mathrm{sin}\:\frac{\left({u}+{v}\right){t}}{{r}},\:{y}_{{C}} ={r}\left(\mathrm{1}−\mathrm{cos}\:\frac{\left({u}+{v}\right){t}}{{r}}\right) \\ $$$${let}\:\alpha=\frac{{ut}}{{r}},\:\beta=\frac{{vt}}{{r}},\:\lambda=\frac{{s}}{{r}} \\ $$$${AB}^{\mathrm{2}} ={s}^{\mathrm{2}} =\left({ut}\right)^{\mathrm{2}} +\left({vt}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${AC}^{\mathrm{2}} ={s}^{\mathrm{2}} ={r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\frac{\left({u}+{v}\right){t}}{{r}}+\left({r}−{r}\:\mathrm{cos}\:\frac{\left({u}+{v}\right){t}}{{r}}−{ut}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\:\mathrm{sin}^{\mathrm{2}} \:\left(\alpha+\beta\right)+\left[\mathrm{1}−\mathrm{cos}\:\left(\alpha+\beta\right)−\alpha\right]^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$${BC}^{\mathrm{2}} ={s}^{\mathrm{2}} =\left({r}\:\mathrm{sin}\:\frac{\left({u}+{v}\right){t}}{{r}}−{vt}\right)^{\mathrm{2}} +\left({r}−{r}\:\mathrm{cos}\:\frac{\left({u}+{v}\right){t}}{{r}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\left[\mathrm{sin}\:\left(\alpha+\beta\right)−\beta\right]^{\mathrm{2}} +\left[\mathrm{1}−\mathrm{cos}\:\left(\alpha+\beta\right)\right]^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\left(\alpha+\beta\right)+\left[\mathrm{1}−\mathrm{cos}\:\left(\alpha+\beta\right)−\alpha\right]^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{1}−\alpha\right)\left[\mathrm{1}−\mathrm{cos}\:\left(\alpha+\beta\right)\right]=\frac{\beta^{\mathrm{2}} }{\mathrm{2}}\:\:\:...\left({I}\right) \\ $$$$\left({i}\right)\:{and}\:\left({iii}\right): \\ $$$$\left[\mathrm{sin}\:\left(\alpha+\beta\right)−\beta\right]^{\mathrm{2}} +\left[\mathrm{1}−\mathrm{cos}\:\left(\alpha+\beta\right)\right]^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\alpha+\beta\right)+\beta\:\mathrm{sin}\:\left(\alpha+\beta\right)=\mathrm{1}−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}\:\:\:...\left({II}\right) \\ $$
Commented by mr W last updated on 28/Nov/24
Commented by mr W last updated on 28/Nov/24

$${these}\:{equations}\:{can}\:{only}\:{be}\:{solved} \\ $$$${nummerically}. \\ $$$${from}\:{the}\:{graph}\:{above}\:{we}\:{can}\:{see} \\ $$$${that}\:{there}\:{is}\:{no}\:{solution}\: \\ $$$$\left({intersection}\:{of}\:{both}\:{curves}\right)\:{when} \\ $$$${A}\:{and}\:{B}\:{move}\:{in}\:{positive}\:{direction}. \\ $$$${there}\:{are}\:{two}\:{solutions}\:{when}\:{they} \\ $$$${move}\:{in}\:{negative}\:{direction}. \\ $$$${following}\:{graphs}\:{show}\:{these}\:{two} \\ $$$${solutions}. \\ $$$$ \\ $$$${solution}\:\mathrm{1}: \\ $$$$\alpha=−\mathrm{0}.\mathrm{2330},\:\beta=−\mathrm{1}.\mathrm{9914} \\ $$$$\frac{{u}}{{v}}=\frac{\alpha}{\beta}\approx\mathrm{0}.\mathrm{117} \\ $$$${solution}\:\mathrm{2}: \\ $$$$\alpha=−\mathrm{2}.\mathrm{5130},\:\beta=−\mathrm{2}.\mathrm{3885} \\ $$$$\frac{{u}}{{v}}=\frac{\alpha}{\beta}\approx\mathrm{0}.\mathrm{741} \\ $$
Commented by mr W last updated on 28/Nov/24
Commented by mr W last updated on 28/Nov/24
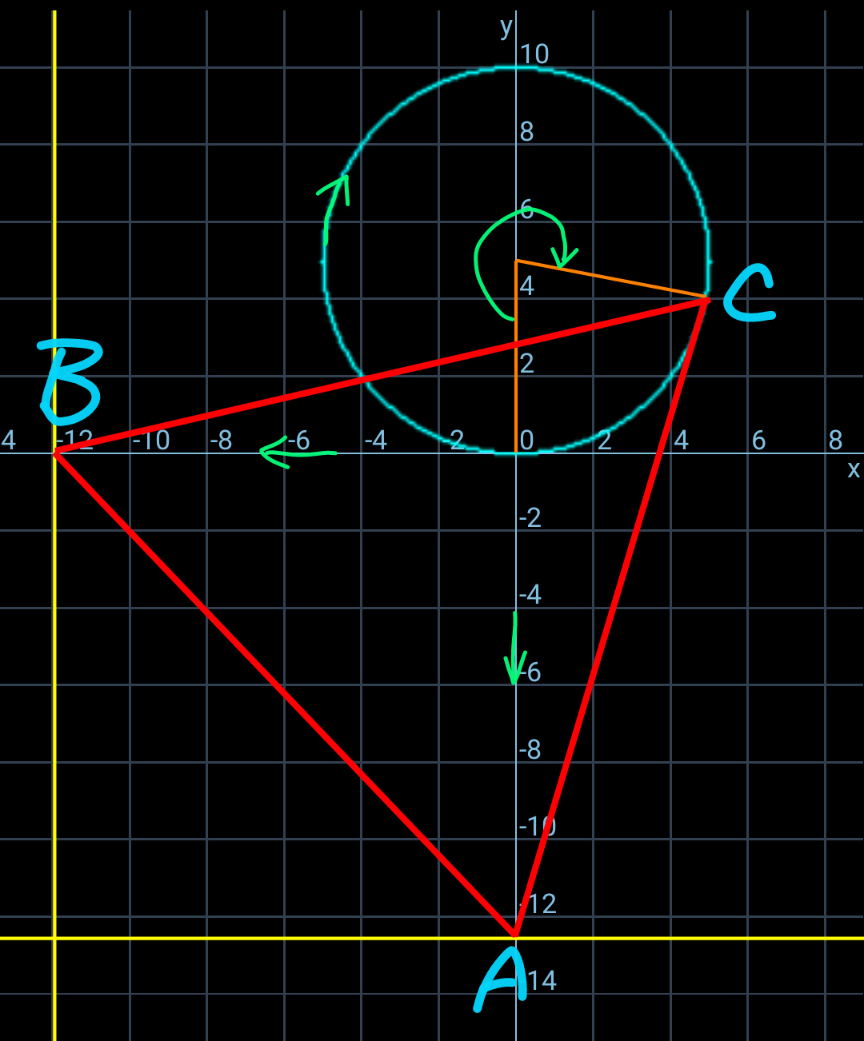
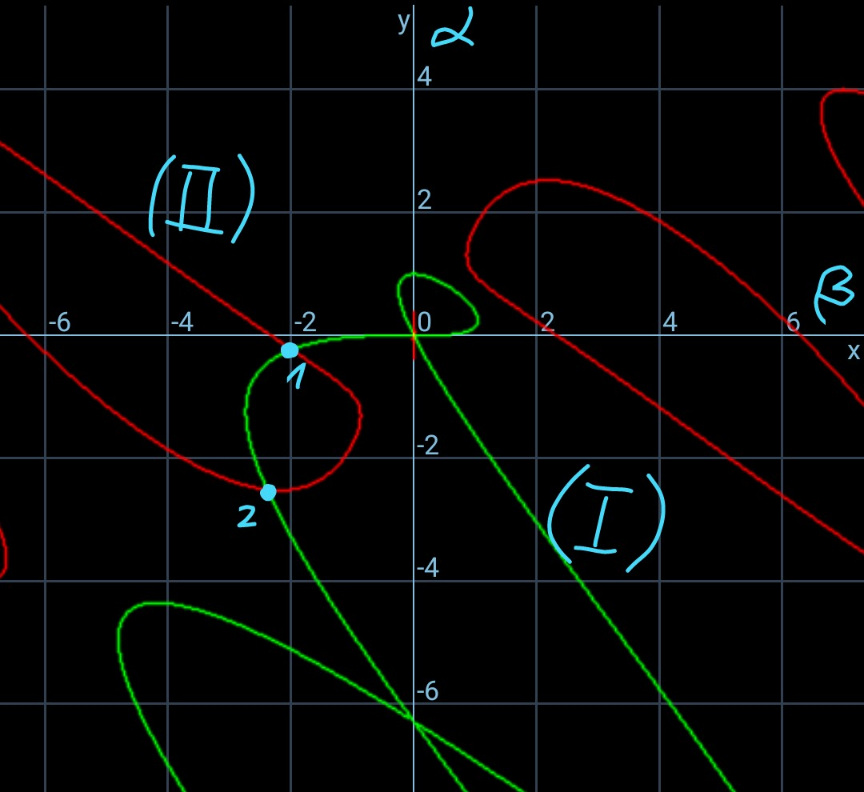
Commented by ajfour last updated on 28/Nov/24
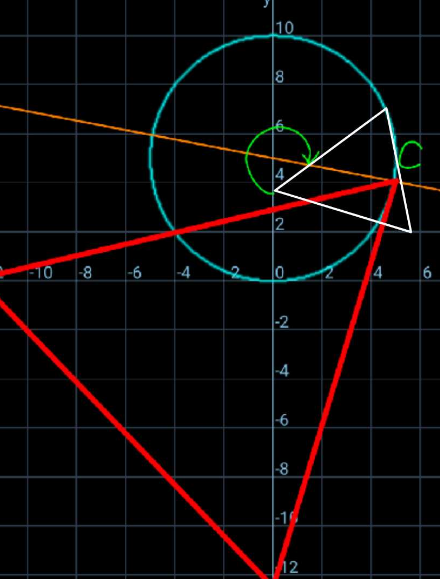
Commented by ajfour last updated on 28/Nov/24
$${Isnt}\:{something}\:{like}\:{this}\:{possible}? \\ $$
Commented by mr W last updated on 28/Nov/24

$${there}\:{are}\:{infinite}\:{equilaterals}.\:{but} \\ $$$${all}\:{three}\:{points}\:{should}\:{reach}\:{the} \\ $$$${vertexes}\:{at}\:{the}\:{same}\:{time}.\:{under} \\ $$$${this}\:{condition}\:{there}\:{are}\:{only}\:{two} \\ $$$${suitable}\:{cases}\:{as}\:{shown}\:{above}. \\ $$
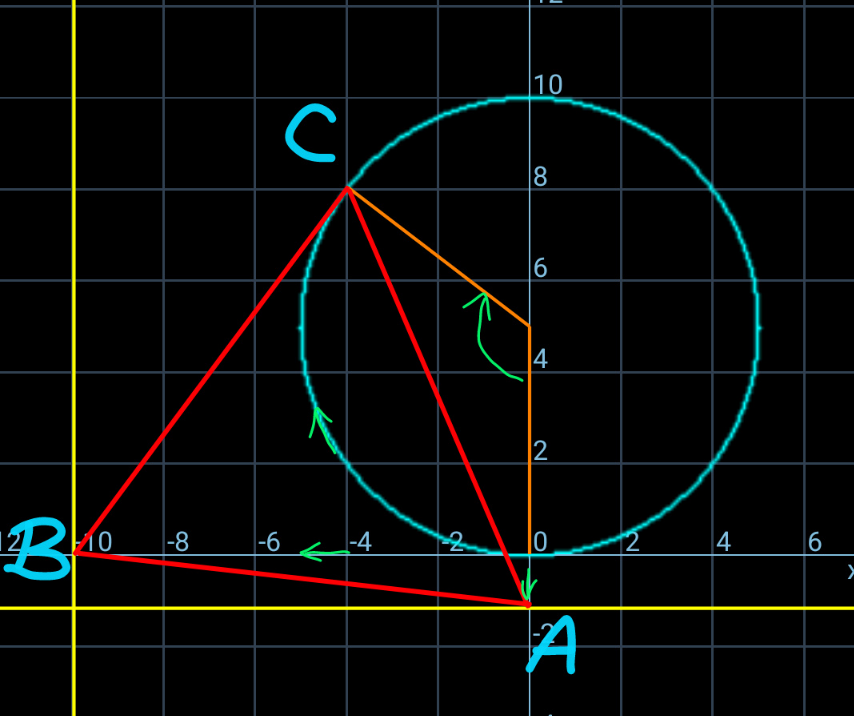
Commented by mr W last updated on 29/Nov/24
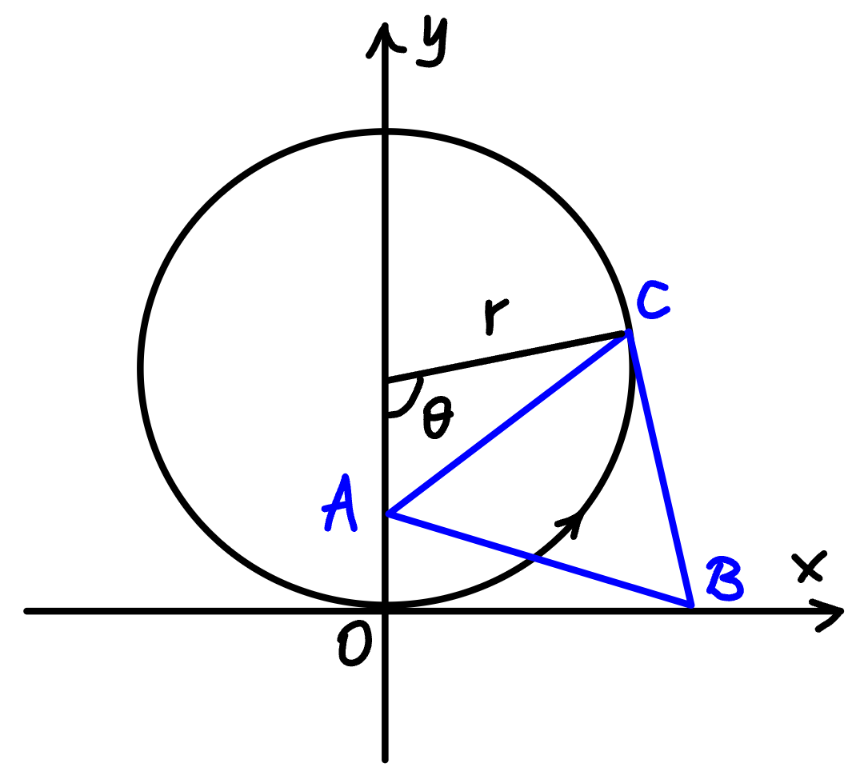
Commented by mr W last updated on 29/Nov/24
$${it}'{s}\:{a}\:{geometric}\:{problem}. \\ $$$$\overset{\frown} {{OC}}=\mid{OA}\mid+\mid{OB}\mid\:{and}\:\mid{AB}\mid=\mid{BC}\mid=\mid{CA}\mid \\ $$
