Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 214072 by Mwamba last updated on 26/Nov/24

Answered by TonyCWX08 last updated on 27/Nov/24

Answered by TonyCWX08 last updated on 27/Nov/24

Consider two points, P and Q. P = (x,y) and Q=(x+δx,y+δy) Let s = length of arc from starting point δs = Length of arc PQ Since δs is very small, we can approximate arc PQ to a straight line. By Pythagoras′s theorem, (δx)^2 +(δy)^2 =(δs)^2 Dividing both sides by (δx)^2 , we get 1+(((δy)/(δx)))^2 =(((δs)/(δx)))^2 As δx→0, this gives 1+((dy/dx))^2 =((ds/dx))^2 Applying Square Root on both sides, (ds/dx)=(√(1+((dy/dx))^2 )) Therefore, we have s=∫(√(1+((dy/dx))^2 ))dx or ∫(√(1+(f′(x))^2 ))dx

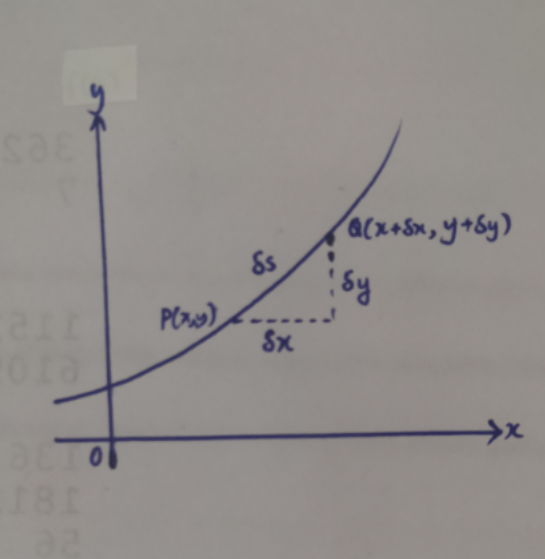
$${Consider}\:{two}\:{points},\:{P}\:{and}\:{Q}. \\ $$$${P}\:=\:\left({x},{y}\right)\:{and}\:{Q}=\left({x}+\delta{x},{y}+\delta{y}\right) \\ $$$${Let}\:{s}\:=\:{length}\:{of}\:{arc}\:{from}\:{starting}\:{point} \\ $$$$\delta{s}\:=\:{Length}\:{of}\:{arc}\:{PQ} \\ $$$$ \\ $$$${Since}\:\delta{s}\:{is}\:{very}\:{small},\:{we}\:{can}\:{approximate}\:{arc}\:{PQ}\:{to}\:{a}\:{straight}\:{line}. \\ $$$${By}\:{Pythagoras}'{s}\:{theorem}, \\ $$$$\left(\delta{x}\right)^{\mathrm{2}} +\left(\delta{y}\right)^{\mathrm{2}} =\left(\delta{s}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${Dividing}\:{both}\:{sides}\:{by}\:\left(\delta{x}\right)^{\mathrm{2}} ,\:{we}\:{get} \\ $$$$\mathrm{1}+\left(\frac{\delta{y}}{\delta{x}}\right)^{\mathrm{2}} =\left(\frac{\delta{s}}{\delta{x}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${As}\:\delta{x}\rightarrow\mathrm{0},\:{this}\:{gives} \\ $$$$\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\left(\frac{{ds}}{{dx}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${Applying}\:{Square}\:{Root}\:{on}\:{both}\:{sides}, \\ $$$$\frac{{ds}}{{dx}}=\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${Therefore},\:{we}\:{have} \\ $$$${s}=\int\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }{dx}\:{or}\:\int\sqrt{\mathrm{1}+\left({f}'\left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$

Answered by TonyCWX08 last updated on 27/Nov/24

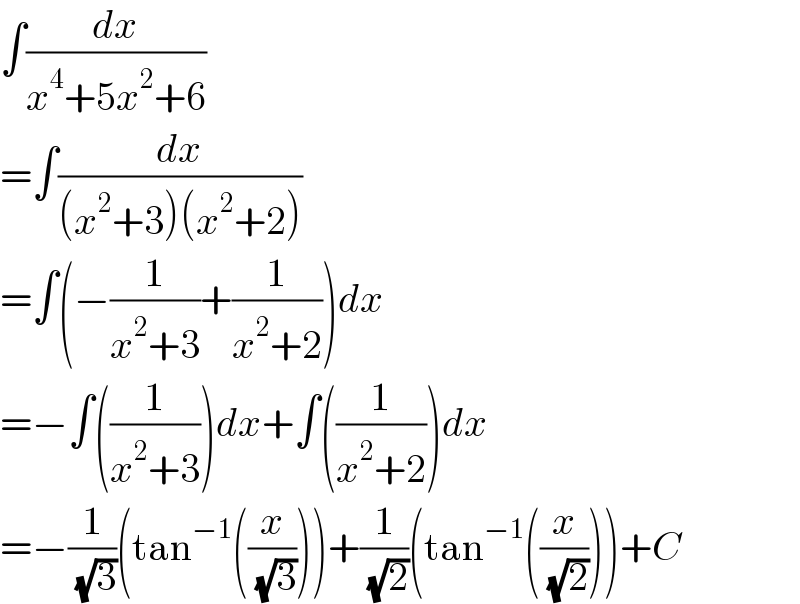
∫(dx/(x^4 +5x^2 +6)) =∫(dx/((x^2 +3)(x^2 +2))) =∫(−(1/(x^2 +3))+(1/(x^2 +2)))dx =−∫((1/(x^2 +3)))dx+∫((1/(x^2 +2)))dx =−(1/( (√3)))(tan^(−1) ((x/( (√3)))))+(1/( (√2)))(tan^(−1) ((x/( (√2)))))+C

$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}} \\ $$$$=\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)} \\ $$$$=\int\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}\right){dx} \\ $$$$=−\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right){dx}+\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right)+{C} \\ $$

Answered by lepuissantcedricjunior last updated on 28/Nov/24

b)((𝛑(3(√2)−2(√3)))/(12))

$$\left.\boldsymbol{{b}}\right)\frac{\boldsymbol{\pi}\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}\right)}{\mathrm{12}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com