Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214059 by RoseAli last updated on 25/Nov/24

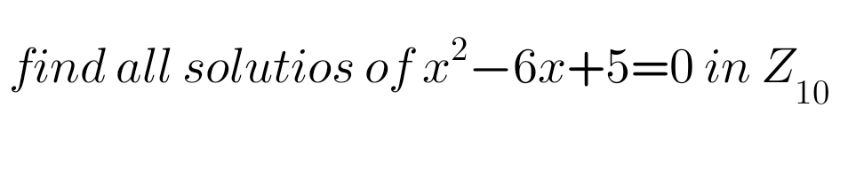
Answered by a.lgnaoui last updated on 25/Nov/24

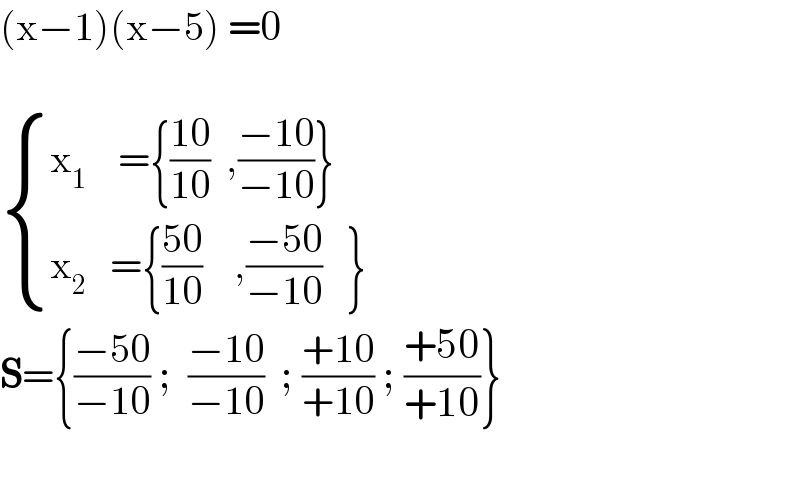
(x−1)(x−5) =0 { ((x_1 ={((10)/(10)) ,((−10)/(−10))})),((x_2 ={((50)/(10)) ,((−50)/(−10)) } )) :} S={((−50)/(−10)) ; ((−10)/(−10)) ; ((+10)/(+10)) ; ((+50)/(+10))}

$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{5}\right)\:=\mathrm{0}\:\:\:\: \\ $$$$\: \\ $$$$\begin{cases}{\mathrm{x}_{\mathrm{1}} \:\:\:\:=\left\{\frac{\mathrm{10}}{\mathrm{10}}\:\:,\frac{−\mathrm{10}}{−\mathrm{10}}\right\}}\\{\mathrm{x}_{\mathrm{2}} \:\:\:=\left\{\frac{\mathrm{50}}{\mathrm{10}}\:\:\:\:,\frac{−\mathrm{50}}{−\mathrm{10}}\:\:\:\right\}\:\:}\end{cases} \\ $$$$\boldsymbol{\mathrm{S}}=\left\{\frac{−\mathrm{50}}{−\mathrm{10}}\:;\:\:\frac{−\mathrm{10}}{−\mathrm{10}}\:\:;\:\frac{+\mathrm{10}}{+\mathrm{10}}\:;\:\frac{+\mathrm{50}}{+\mathrm{10}}\right\} \\ $$$$ \\ $$

Answered by A5T last updated on 25/Nov/24

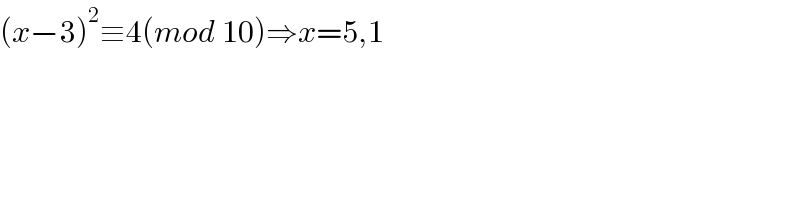
(x−3)^2 ≡4(mod 10)⇒x=5,1

$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} \equiv\mathrm{4}\left({mod}\:\mathrm{10}\right)\Rightarrow{x}=\mathrm{5},\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com