Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 214047 by ajfour last updated on 25/Nov/24

Commented by ajfour last updated on 25/Nov/24

The L shaped rigid scale can turn about the pivot on a frictionless table. The small mass m hits and after rebounding happens to find the other end. Find θ, if α is measured. (Take coefficient of restitution e)

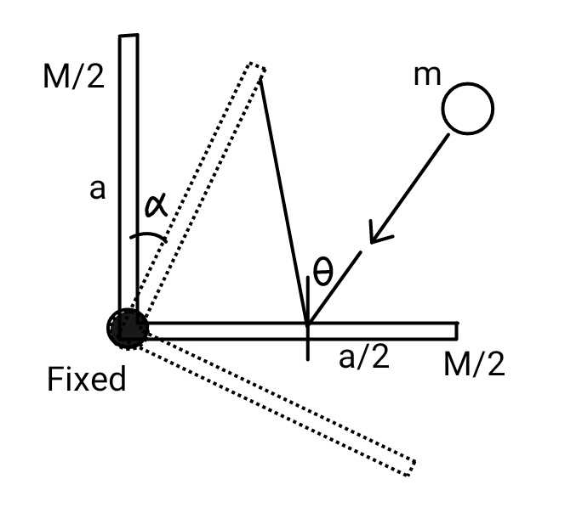
$$\:{The}\:{L}\:{shaped}\:{rigid}\:{scale}\:{can}\:{turn}\: \\ $$$${about}\:{the}\:{pivot}\:{on}\:{a}\:{frictionless}\:{table}. \\ $$$$\:{The}\:{small}\:{mass}\:{m}\:{hits}\:{and}\:{after}\: \\ $$$${rebounding}\:{happens}\:{to}\:{find}\:{the} \\ $$$$\:{other}\:{end}.\:{Find}\:\theta,\:{if}\:\alpha\:{is}\:{measured}. \\ $$$$\left({Take}\:{coefficient}\:{of}\:{restitution}\:\boldsymbol{{e}}\right) \\ $$

Answered by mr W last updated on 25/Nov/24

Commented by mr W last updated on 27/Nov/24

u=velocity of ball before collision v=velocity of ball after collision ω=angular velocity of L−frame after collision u sin θ=v sin φ ...(i) e=((v cos φ+((ωl)/2))/(u cos θ)) ⇒eu cos θ=v cos φ+((lω)/2) ...(ii) mu cos θ×(l/2)=((Ml^2 ω)/3)−mv cos φ×(l/2) ⇒u cos θ+v cos φ=((2Mlω)/(3m)) ...(iii) t=(α/ω) (l/2)−l sin α=v sin φ×t ((lω)/α)((1/2)−sin α)=v sin φ ⇒((1/(2α))−((sin α)/α))lω=u sin θ ...(iv) l cos α=v cos φ ×t ((lω cos α)/α)=v cos φ ...(v) we have 5 equations for 6 variables: u, v, ω, θ, φ, α (iii): u cos θ+((lω cos α)/α)=((2Mlω)/(3m)) (((2M)/(3m))−((cos α)/α))lω=u cos θ ...(vi) (v) into (ii): eu cos θ=((lω cos α)/α)+((lω)/2) ⇒(((cos α)/α)+(1/2))((lω)/e)=u cos θ from (vi): (((cos α)/α)+(1/2))((lω)/e)=(((2M)/(3m))−((cos α)/α))lω (1+(1/e))((cos α)/α)=((2M)/(3m))−(1/(2e)) ⇒((cos α)/α)=((((2M)/(3m))−(1/(2e)))/(1+(1/e))) ...(vii) since α<(π/6), ((((2M)/(3m))−(1/(2e)))/(1+(1/e)))>(((√3)×6)/(2×π)) ⇒ (M/m)>((9(√3)(1+(1/e)))/(2π))+(3/(4e)) (iv)/(vi): (((1/(2α))−((sin α)/α))/(((2M)/(3m))−((cos α)/α)))=tan θ ⇒θ=tan^(−1) (((1/2)−sin α)/(((2αM)/(3m))−cos α)) ...(viii) from (iv): ((lω)/u)=((α sin θ)/((1/2)−sin α)) ...(ix) (i)^2 +(v)^2 : (u sin θ)^2 +(((lω cos α)/α))^2 =v^2 (v^2 /u^2 )=sin^2 θ+(((lω)/u))^2 (((cos α)/α))^2 ⇒(v/u)=sin θ(√(1+((α/((1/2)−sin α)))^2 (((((2M)/(3m))−(1/(2e)))/(1+(1/e))))^2 )) ...(x) (i)/(v): ((u sin θ)/((lω cos α)/α))=tan φ tan φ=((sin θ)/((((lω)/u))(((cos α)/α))))=((((1/2)−sin α)/α))(((1+(1/e))/(((2M)/(3m))−(1/(2e))))) ⇒φ=tan^(−1) ((((1/2)−sin α)/α))(((1+(1/e))/(((2M)/(3m))−(1/(2e))))) ...(xi)

$${u}={velocity}\:{of}\:{ball}\:{before}\:{collision} \\ $$$${v}={velocity}\:{of}\:{ball}\:{after}\:{collision} \\ $$$$\omega={angular}\:{velocity}\:{of}\:{L}−{frame} \\ $$$$\:\:\:\:\:\:\:{after}\:{collision} \\ $$$${u}\:\mathrm{sin}\:\theta={v}\:\mathrm{sin}\:\phi\:\:\:...\left({i}\right) \\ $$$${e}=\frac{{v}\:\mathrm{cos}\:\phi+\frac{\omega{l}}{\mathrm{2}}}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{eu}\:\mathrm{cos}\:\theta={v}\:\mathrm{cos}\:\phi+\frac{{l}\omega}{\mathrm{2}}\:\:\:...\left({ii}\right) \\ $$$${mu}\:\mathrm{cos}\:\theta×\frac{{l}}{\mathrm{2}}=\frac{{Ml}^{\mathrm{2}} \omega}{\mathrm{3}}−{mv}\:\mathrm{cos}\:\phi×\frac{{l}}{\mathrm{2}} \\ $$$$\Rightarrow{u}\:\mathrm{cos}\:\theta+{v}\:\mathrm{cos}\:\phi=\frac{\mathrm{2}{Ml}\omega}{\mathrm{3}{m}}\:\:\:...\left({iii}\right) \\ $$$${t}=\frac{\alpha}{\omega} \\ $$$$\frac{{l}}{\mathrm{2}}−{l}\:\mathrm{sin}\:\alpha={v}\:\mathrm{sin}\:\phi×{t} \\ $$$$\frac{{l}\omega}{\alpha}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha\right)={v}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}\alpha}−\frac{\mathrm{sin}\:\alpha}{\alpha}\right){l}\omega={u}\:\mathrm{sin}\:\theta\:\:\:...\left({iv}\right) \\ $$$${l}\:\mathrm{cos}\:\alpha={v}\:\mathrm{cos}\:\phi\:×{t} \\ $$$$\frac{{l}\omega\:\mathrm{cos}\:\alpha}{\alpha}={v}\:\mathrm{cos}\:\phi\:\:\:...\left({v}\right) \\ $$$${we}\:{have}\:\mathrm{5}\:{equations}\:{for}\:\mathrm{6}\:{variables}: \\ $$$${u},\:{v},\:\omega,\:\theta,\:\phi,\:\alpha \\ $$$$ \\ $$$$\left({iii}\right): \\ $$$${u}\:\mathrm{cos}\:\theta+\frac{{l}\omega\:\mathrm{cos}\:\alpha}{\alpha}=\frac{\mathrm{2}{Ml}\omega}{\mathrm{3}{m}} \\ $$$$\left(\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{cos}\:\alpha}{\alpha}\right){l}\omega={u}\:\mathrm{cos}\:\theta\:\:\:...\left({vi}\right) \\ $$$$\left({v}\right)\:{into}\:\left({ii}\right): \\ $$$${eu}\:\mathrm{cos}\:\theta=\frac{{l}\omega\:\mathrm{cos}\:\alpha}{\alpha}+\frac{{l}\omega}{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{\mathrm{cos}\:\alpha}{\alpha}+\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{{l}\omega}{{e}}={u}\:\mathrm{cos}\:\theta \\ $$$${from}\:\left({vi}\right): \\ $$$$\left(\frac{\mathrm{cos}\:\alpha}{\alpha}+\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{{l}\omega}{{e}}=\left(\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{cos}\:\alpha}{\alpha}\right){l}\omega \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}\right)\frac{\mathrm{cos}\:\alpha}{\alpha}=\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\alpha}{\alpha}=\frac{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}{\mathrm{1}+\frac{\mathrm{1}}{{e}}}\:\:\:...\left({vii}\right) \\ $$$${since}\:\alpha<\frac{\pi}{\mathrm{6}},\:\:\frac{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}{\mathrm{1}+\frac{\mathrm{1}}{{e}}}>\frac{\sqrt{\mathrm{3}}×\mathrm{6}}{\mathrm{2}×\pi} \\ $$$$\Rightarrow\:\frac{{M}}{{m}}>\frac{\mathrm{9}\sqrt{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}\right)}{\mathrm{2}\pi}+\frac{\mathrm{3}}{\mathrm{4}{e}} \\ $$$$\left({iv}\right)/\left({vi}\right): \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}\alpha}−\frac{\mathrm{sin}\:\alpha}{\alpha}}{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{cos}\:\alpha}{\alpha}}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}{\frac{\mathrm{2}\alpha{M}}{\mathrm{3}{m}}−\mathrm{cos}\:\alpha}\:\:\:...\left({viii}\right) \\ $$$${from}\:\left({iv}\right): \\ $$$$\frac{{l}\omega}{{u}}=\frac{\alpha\:\mathrm{sin}\:\theta}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}\:\:\:...\left({ix}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} +\left({v}\right)^{\mathrm{2}} : \\ $$$$\left({u}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left(\frac{{l}\omega\:\mathrm{cos}\:\alpha}{\alpha}\right)^{\mathrm{2}} ={v}^{\mathrm{2}} \\ $$$$\frac{{v}^{\mathrm{2}} }{{u}^{\mathrm{2}} }=\mathrm{sin}^{\mathrm{2}} \:\theta+\left(\frac{{l}\omega}{{u}}\right)^{\mathrm{2}} \left(\frac{\mathrm{cos}\:\alpha}{\alpha}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{v}}{{u}}=\mathrm{sin}\:\theta\sqrt{\mathrm{1}+\left(\frac{\alpha}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}\right)^{\mathrm{2}} \left(\frac{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}{\mathrm{1}+\frac{\mathrm{1}}{{e}}}\right)^{\mathrm{2}} }\:\:\:...\left({x}\right) \\ $$$$\left({i}\right)/\left({v}\right): \\ $$$$\frac{{u}\:\mathrm{sin}\:\theta}{\frac{{l}\omega\:\mathrm{cos}\:\alpha}{\alpha}}=\mathrm{tan}\:\phi \\ $$$$\mathrm{tan}\:\phi=\frac{\mathrm{sin}\:\theta}{\left(\frac{{l}\omega}{{u}}\right)\left(\frac{\mathrm{cos}\:\alpha}{\alpha}\right)}=\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}{\alpha}\right)\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{e}}}{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}\right)\: \\ $$$$\Rightarrow\phi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}{\alpha}\right)\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{e}}}{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}\right)\:\:\:...\left({xi}\right) \\ $$

Commented by mr W last updated on 27/Nov/24

example: (M/m)=8, e=0.75 ⇒α≈0.3370≈19.31° ⇒θ≈0.1958≈11.22° ⇒φ≈0.2462≈14.11° ⇒(v/u)≈0.7986 ⇒((lω)/u)≈0.3873

$${example}: \\ $$$$\frac{{M}}{{m}}=\mathrm{8},\:{e}=\mathrm{0}.\mathrm{75} \\ $$$$\Rightarrow\alpha\approx\mathrm{0}.\mathrm{3370}\approx\mathrm{19}.\mathrm{31}° \\ $$$$\Rightarrow\theta\approx\mathrm{0}.\mathrm{1958}\approx\mathrm{11}.\mathrm{22}° \\ $$$$\Rightarrow\phi\approx\mathrm{0}.\mathrm{2462}\approx\mathrm{14}.\mathrm{11}° \\ $$$$\Rightarrow\frac{{v}}{{u}}\approx\mathrm{0}.\mathrm{7986} \\ $$$$\Rightarrow\frac{{l}\omega}{{u}}\approx\mathrm{0}.\mathrm{3873} \\ $$

Commented by ajfour last updated on 26/Nov/24

s^2 =l^2 +(l^2 /4)−(l^2 /2)sin α s^2 =(l^2 /4)(3−2sin α)=v^2 ((α^2 /ω^2 )) ⇒ (s/(αl))=(v/(ωl))=((√(3−2sin α))/(2α)) mu((l/2)cos θ)=((Ml^2 ω)/3)−mv((l/2))cos φ usin θ=vsin φ & m((u/v))((l/2)cos θ)=((Ml^2 )/3)((ω/v))−mcos φ((l/2)) ((sin φcos θ)/(sin θ))+cos φ=((2M)/(3m))(((αl)/s)) cot θ((l/2)−lsin α)+lcos α=(((2M)/(3m)))αl cot θ=(((((2M)/(3m)))α−cos α)/((1/2)−sin α)) tan θ = (((1/2)−sin α)/((((2M)/(3m)))α−cos α))

$${s}^{\mathrm{2}} ={l}^{\mathrm{2}} +\frac{{l}^{\mathrm{2}} }{\mathrm{4}}−\frac{{l}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}\:\alpha \\ $$$${s}^{\mathrm{2}} =\frac{{l}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{3}−\mathrm{2sin}\:\alpha\right)={v}^{\mathrm{2}} \left(\frac{\alpha^{\mathrm{2}} }{\omega^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\frac{{s}}{\alpha{l}}=\frac{{v}}{\omega{l}}=\frac{\sqrt{\mathrm{3}−\mathrm{2sin}\:\alpha}}{\mathrm{2}\alpha} \\ $$$${mu}\left(\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta\right)=\frac{{Ml}^{\mathrm{2}} \omega}{\mathrm{3}}−{mv}\left(\frac{{l}}{\mathrm{2}}\right)\mathrm{cos}\:\phi \\ $$$${u}\mathrm{sin}\:\theta={v}\mathrm{sin}\:\phi \\ $$$$\& \\ $$$${m}\left(\frac{{u}}{{v}}\right)\left(\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta\right)=\frac{{Ml}^{\mathrm{2}} }{\mathrm{3}}\left(\frac{\omega}{{v}}\right)−{m}\mathrm{cos}\:\phi\left(\frac{{l}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{sin}\:\phi\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}+\mathrm{cos}\:\phi=\frac{\mathrm{2}{M}}{\mathrm{3}{m}}\left(\frac{\alpha{l}}{{s}}\right) \\ $$$$\mathrm{cot}\:\theta\left(\frac{{l}}{\mathrm{2}}−{l}\mathrm{sin}\:\alpha\right)+{l}\mathrm{cos}\:\alpha=\left(\frac{\mathrm{2}{M}}{\mathrm{3}{m}}\right)\alpha{l} \\ $$$$\mathrm{cot}\:\theta=\frac{\left(\frac{\mathrm{2}{M}}{\mathrm{3}{m}}\right)\alpha−\mathrm{cos}\:\alpha}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\alpha}{\left(\frac{\mathrm{2}{M}}{\mathrm{3}{m}}\right)\alpha−\mathrm{cos}\:\alpha}\:\:\: \\ $$

Commented by ajfour last updated on 26/Nov/24

yeah! And I got the same, another way, Sir.

Commented by mr W last updated on 26/Nov/24

can you please check following: α is not independent. it is given through ((cos α)/α)=((((2M)/(3m))−(1/(2e)))/(1+(1/e)))

$${can}\:{you}\:{please}\:{check}\:{following}: \\ $$$$\alpha\:{is}\:{not}\:{independent}.\:{it}\:{is}\:{given} \\ $$$${through} \\ $$$$\frac{\mathrm{cos}\:\alpha}{\alpha}=\frac{\frac{\mathrm{2}{M}}{\mathrm{3}{m}}−\frac{\mathrm{1}}{\mathrm{2}{e}}}{\mathrm{1}+\frac{\mathrm{1}}{{e}}} \\ $$

Commented by ajfour last updated on 26/Nov/24

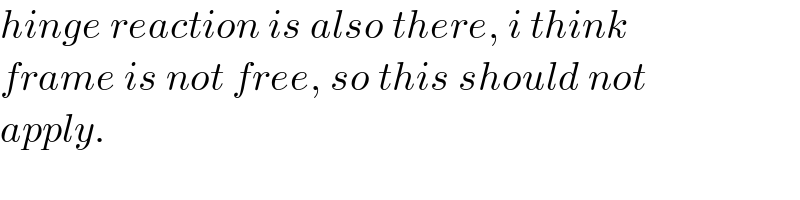
hinge reaction is also there, i think frame is not free, so this should not apply.

$${hinge}\:{reaction}\:{is}\:{also}\:{there},\:{i}\:{think} \\ $$$${frame}\:{is}\:{not}\:{free},\:{so}\:{this}\:{should}\:{not} \\ $$$${apply}. \\ $$

Commented by mr W last updated on 26/Nov/24

see above

$${see}\:{above} \\ $$

Commented by ajfour last updated on 27/Nov/24

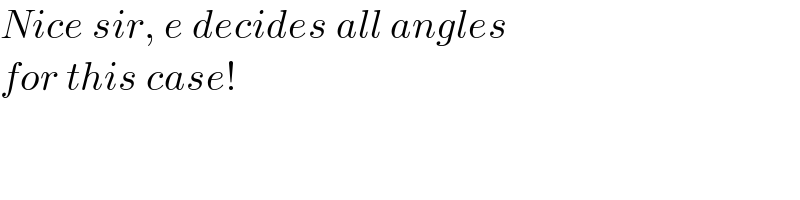
Nice sir, e decides all angles for this case!

$${Nice}\:{sir},\:{e}\:{decides}\:{all}\:{angles}\: \\ $$$${for}\:{this}\:{case}! \\ $$

Commented by mr W last updated on 27/Nov/24

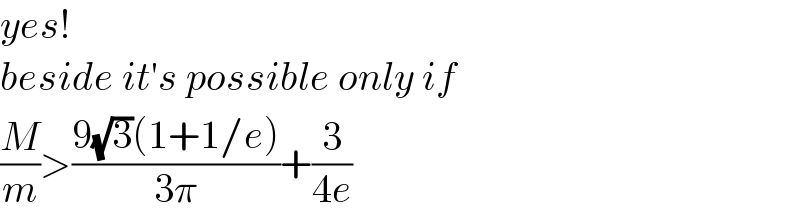
yes! beside it′s possible only if (M/m)>((9(√3)(1+1/e))/(3π))+(3/(4e))

$${yes}! \\ $$$${beside}\:{it}'{s}\:{possible}\:{only}\:{if} \\ $$$$\frac{{M}}{{m}}>\frac{\mathrm{9}\sqrt{\mathrm{3}}\left(\mathrm{1}+\mathrm{1}/{e}\right)}{\mathrm{3}\pi}+\frac{\mathrm{3}}{\mathrm{4}{e}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com